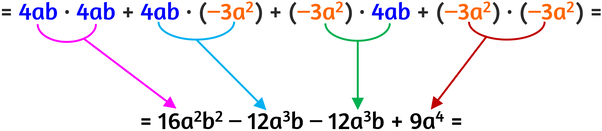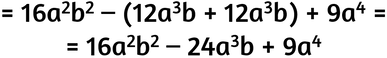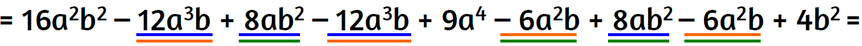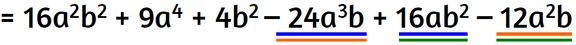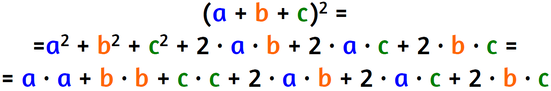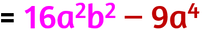I PRODOTTI NOTEVOLI
|
Si chiamano prodotti notevoli tutte quelle moltiplicazioni tra polinomi, e potenze di polinomi, il cui risultato, prodotto, può essere ricavato attraverso stratagemmi meno lunghi che normalmente non necessitano di semplificazioni successive.
Per chi avesse difficoltà ad applicare le regole dei prodotti notevoli, ricordo che le potenze possono essere scritte come moltiplicazione e risolte come prodotto di un polinomio per un polinomio (nel caso dei quadrati e dei cubi il polinomio è sempre lo stesso).
IMPORTANTE: dopo aver risolto qualunque prodotto semplice o notevole ricordati di scrivere il risultato in forma normale (non ci devono essere monomi simili). |
I prodotti notevoli più studiati sono:
- il quadrato di un binomio;
- il quadrato di un trinomio;
- la potenza ennesima di un binomio (applicando il triangolo di Tartaglia);
- il prodotto della somma di un binomio per la sua differenza;
- il cubo di un binomio.
Quadrato di un binomio
Se un binomio è moltiplicato per se stesso, può essere scritto come il quadrato di quel binomio.
(🧡 + 💎) · (🧡 + 💎) = (🧡 + 💎)² =
Siamo di fronte ad un quadrato che ha come lato la somma o la differenza di due monomi.
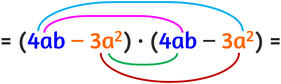
Supponiamo di voler risolvere il seguente quadrato di un binomio:
Scriviamo la potenza come moltiplicazione
Il primo monomio della prima parentesi moltiplica entrambi i monomi della seconda parentesi, poi il secondo monomio della prima parentesi moltiplica entrami i monomi della seconda parentesi.
Metti insieme i monomi simili.
Alla fine ottieni sempre un trinomio.
Alla fine ottieni sempre un trinomio.
Formula ridotta per calcolare il valore del quadrato di un binomio:
Il valore del quadrato di un binomio lo si ricava facendo:
- il quadrato del primo monomio (il primo monomio × il primo monomio);
- il quadrato del secondo monomio (il secondo monomio × il secondo monomio);
- il doppio prodotto del primo monomio per il secondo monomio
(2 × primo monomio × secondo monomio).
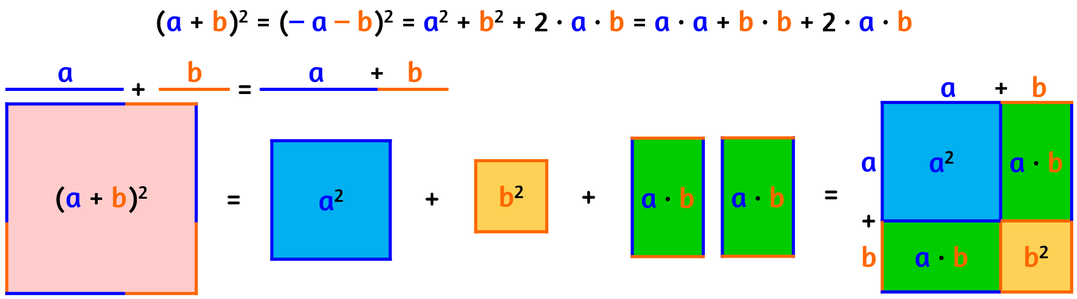
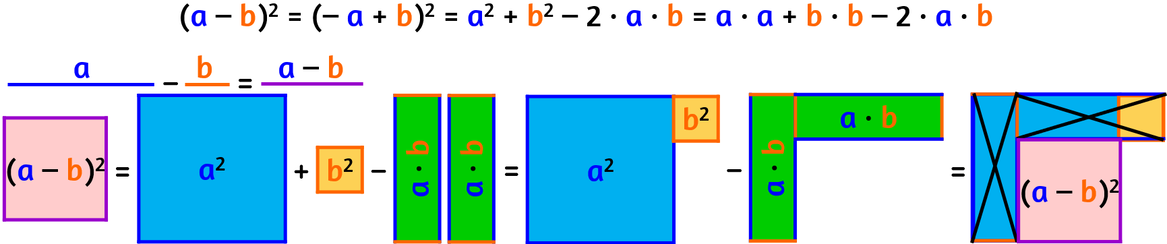
GIUSTIFICAZIONE GEOMETRICA
Primo e secondo monomio concordi (entrambi positivi o entrambi negativi).
Tutti e tre i termini sono positivi.
Tutti e tre i termini sono positivi.
Primo e secondo monomio discordi (uno positivo e l’altro negativo).
I due quadrati sono positivi, mentre il doppio prodotto è negativo.
I due quadrati sono positivi, mentre il doppio prodotto è negativo.
IMPORTANTE
I quadrati sono sempre POSITIVI (cioè sempre preceduti dal segno +)
Il doppio prodotto (due volte il primo per il secondo termine) sarà:
I quadrati sono sempre POSITIVI (cioè sempre preceduti dal segno +)
Il doppio prodotto (due volte il primo per il secondo termine) sarà:
- positivo (preceduto dal segno +) se il binomio è concorde (hanno lo stesso segno, entrambi positivi o entrambi negativi)
- negativo (preceduto dal segno -) se il binomio è discorde (hanno segno diverso, uno è positivo e l'altro negativo o viceversa)
Quadrato di un trinomio
Siamo di fronte ad un quadrato che ha come lato la somma algebrica di tre monomi.
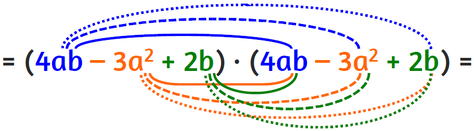
Supponiamo di voler risolvere il seguente quadrato di un trinomio:
Scriviamo la potenza come moltiplicazione.
Ciascun monomio della prima parentesi moltiplica ciascun monomio della seconda parentesi.
Metti insieme i monomi simili.
Alla fine ottieni polinomio composto da 6 monomi.
Alla fine ottieni polinomio composto da 6 monomi.
Da qui la regola, il valore del quadrato di un binomio lo si ricava facendo:
- il quadrato del primo monomio (il primo monomio × il primo monomio);
- il quadrato del secondo monomio (il secondo monomio × il secondo monomio);
- il quadrato del terzo monomio (il terzo monomio × il terzo monomio);
- il doppio prodotto del primo monomio per il secondo monomio
(2 × primo monomio × secondo monomio). - il doppio prodotto del primo monomio per il terzo monomio
(2 × primo monomio × terzo monomio). - il doppio prodotto del secondo monomio per il terzo monomio
(2 × secondo monomio × terzo monomio).
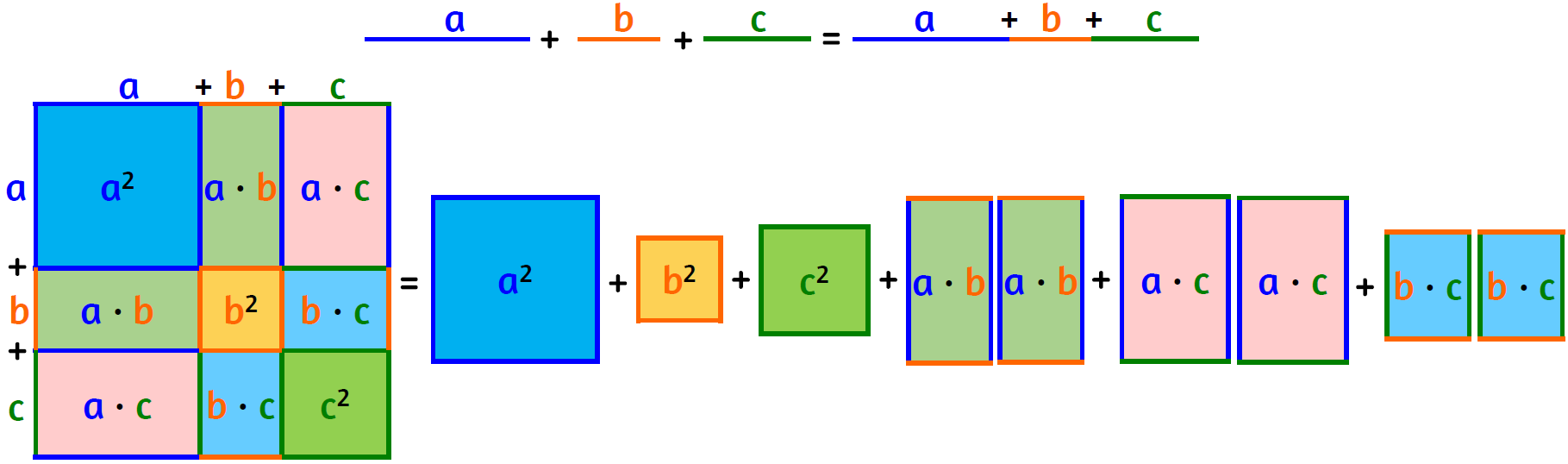
GIUSTIFICAZIONE GEOMETRICA
Il cubo di un binomio
Siamo di fronte ad un binomio moltiplicato per se stesso tre volte.
Sono esempi di cubo del binomio:
(🧡 + 💎) (🧡 + 💎) (🧡 + 💎)
(🧡 + 💎)² · (🧡 + 💎) = (🧡 + 💎) · (🧡 + 💎)²
(🧡 + 💎)³
(🧡 + 💎)² · (🧡 + 💎) = (🧡 + 💎) · (🧡 + 💎)²
(🧡 + 💎)³
Il binomio può essere sia concorde che discorde.
Vediamo di calcolarlo come prodotto di un binomio per se stesso tre volte:
(🧡 + 💎) (🧡 + 💎) (🧡 + 💎) =
Calcola il prodotto dei primi due binomi lasciando il loro risultato dentro delle parentesi tonde, perché poi moltiplicherà il prossimo binomio:
= [🧡 (🧡 + 💎) + 💎 (🧡 + 💎)] (🧡 + 💎) =
= [🧡 · 🧡 + 🧡 · 💎 + 🧡 · 💎 + 💎 · 💎] (🧡 + 💎) =
= [🧡 · 🧡 + 🧡 · 💎 + 🧡 · 💎 + 💎 · 💎] (🧡 + 💎) =
Esegui i prodotti e metti insieme i termini simili, lasciando dentro una parentesi il risultato:
= [🧡² + 2 · 🧡 · 💎 + 💎²] (🧡 + 💎) =
Riapplica la proprietà distributiva moltiplicando ogni termine del primo polinomio per entrambi i termini del binomio successivo:
= 🧡² · (🧡 + 💎) + 2 · 🧡 · 💎 · (🧡 + 💎) + 💎² · (🧡 + 💎) =
Esegui le moltiplicazioni:
= 🧡² · 🧡 + 🧡² · 💎 + 2 · 🧡 · 💎 · 🧡 + 2 · 🧡 · 💎 · 💎 + 💎² · 🧡 + 💎² · 💎 =
= 🧡³ + 🧡² ·💎 + 2 · 🧡² ·💎 + 2 · 🧡 · 💎² + 🧡 ·💎² + 💎³ =
= 🧡³ + 🧡² ·💎 + 2 · 🧡² ·💎 + 2 · 🧡 · 💎² + 🧡 ·💎² + 💎³ =
Metti insieme i termini simili:
= 🧡³ + 3 · 🧡² ·💎 + 3 · 🧡 · 💎² + 💎³
MA QUANTI PASSAGGI PER TROVARE IL RISULTATO?!
Non è necessario fare tutti questi passaggi ma applicare una "formula ridotta", infatti si tratta di un prodotto notevole e come tale ha delle caratteristiche per ti permettono di calcolarlo senza "giri troppo lunghi":
il primo × il primo × il primo;
Il triangolo di Tartaglia e l'ennesima potenza di un binomio
Il triangolo di Tartaglia (o di Pascal) è il celeberrimo triangolo che racchiude in sé una moltitudine di caratteristiche, tra le quali i coefficienti dei singoli monomi che compongono la potenza ennesima di un binomio.
Potenza 0 di un binomio
Se un binomio è elevato zero, il risultato sarà sempre 1, farà eccezione il caso in cui il valore del binomio sia uguale a zero (in questo caso non avrà significato).
Potenza prima di un binomio
Se un binomio è elevato 1, il risultato sarà uguale al binomio stesso.
Binomio al quadrato o quadrato del binomio
Un binomio al quadrato sarà uguale a:
- una volta il quadrato del primo termine
- 2 volte il prodotto del primo per il secondo termine
- una volta il quadrato del secondo termine
Binomio al cubo o cubo del binomio
Il cubo di un binomio sarà uguale a:
- una volta il primo termine al cubo (moltiplica il primo termine per se stesso tre volte)
- 3 volte il primo termine al quadrato per il secondo termine
- 3 volte il primo termine per il secondo termine al quadrato
- una volta il secondo termine al cubo (moltiplica il secondo termine per se stesso tre volte)
La quarta potenza di un binomio
- una volta il primo termine elevato 4 (moltiplica il primo termine per se stesso quattro volte)
- 4 volte il primo termine al cubo (elevato tre) per il secondo termine semplice
- 6 volte il primo termine al quadrato (elevato due) per il secondo termine al quadrato
- 4 volte il primo termine per il secondo termine al cubo (elevato tre)
- una volta il secondo termine elevato 4 (moltiplica il secondo termine per se stesso quattro volte)
Prodotto di una somma per la loro differenza
Siamo di fronte al prodotto di due monomi, così formato:
(a + b)(a – b) oppure (a + b)(– a + b) oppure (– a – b)(a – b) oppure (– a – b)(– a + b), dove con a si indica un monomio e con b se ne indica un altro.
Ma cosa accomuna questi prodotti?
In ciascun prodotto sono presenti due monomi uguali e due monomi opposti.
Si chiama:
(a + b)(a – b) oppure (a + b)(– a + b) oppure (– a – b)(a – b) oppure (– a – b)(– a + b), dove con a si indica un monomio e con b se ne indica un altro.
Ma cosa accomuna questi prodotti?
In ciascun prodotto sono presenti due monomi uguali e due monomi opposti.
Si chiama:
- prodotto → il risultato di una moltiplicazione
- di una somma → perché entrambi i monomi sono positivi o negativi → (a + b) oppure (– a – b)
- di una differenza → perché i monomi sono opposti → (a – b) oppure (– a + b)
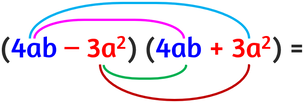
Supponiamo di voler risolvere la seguente somma per differenza:
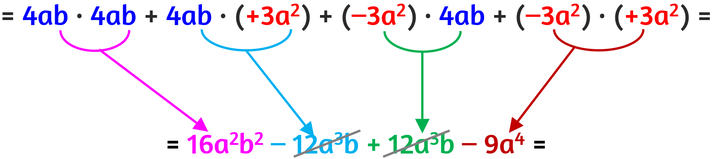
Il primo monomio della prima parentesi moltiplica entrambi i monomi della seconda parentesi. Poi il secondo monomio della prima parentesi moltiplica entrami i monomi della seconda parentesi.
Svolgi le moltiplicazioni.
Metti insieme i monomi simili e cancella gli opposti.
Alla fine ottieni sempre un binomio.
Metti insieme i monomi simili e cancella gli opposti.
Alla fine ottieni sempre un binomio.
Da qui la regola, il valore del quadrato di un binomio lo si ricava facendo:
- + monomio uguale × monomio uguale → sempre positivo
- – monomio opposto × monomio opposto → sempre negativo
Ottieni sempre la differenza di due quadrati.
Se il monomio uguale è il primo termine mentre i monomi opposti sono il secondo termine, avremo:
(a + b)(a – b) = (– a – b)(– a + b) = a² – b²
dove il primo termine al quadrato è positivo, mentre il secondo termine al quadrato è negativo.
Se il monomio uguale è il secondo termine mentre i monomi opposti sono il primo termine, avremo:
(a + b)(– a + b) = (– a – b)(a – b) = – a² + b²
dove il primo termine al quadrato è negativo, mentre il secondo termine al quadrato è positivo.
|
|
contatore inserito il 15 luglio 2021
|