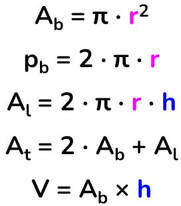I POLIEDRI E I SOLIDI DI ROTAZIONE
Caratteristiche generali a tutti i poliedri
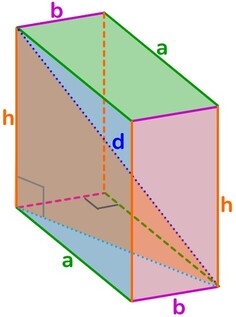
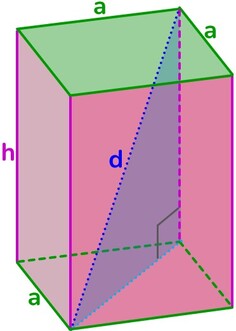
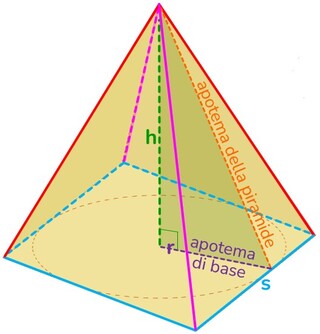
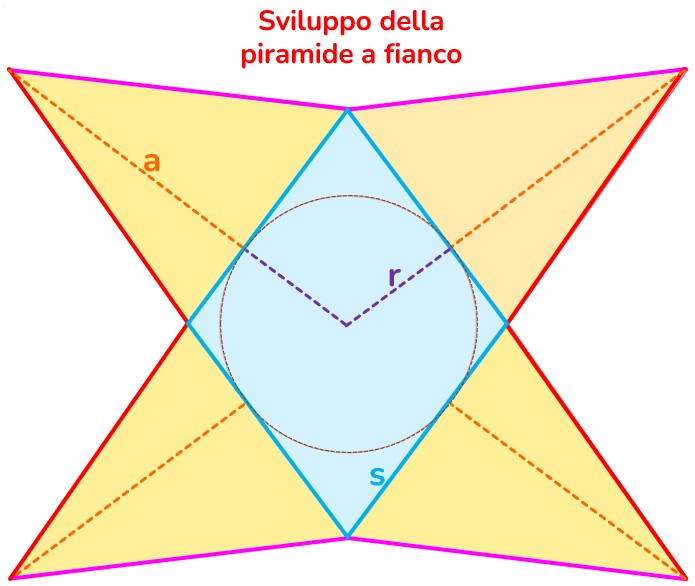
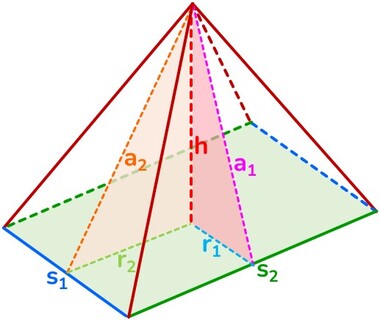
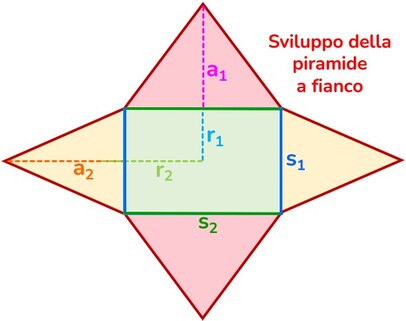
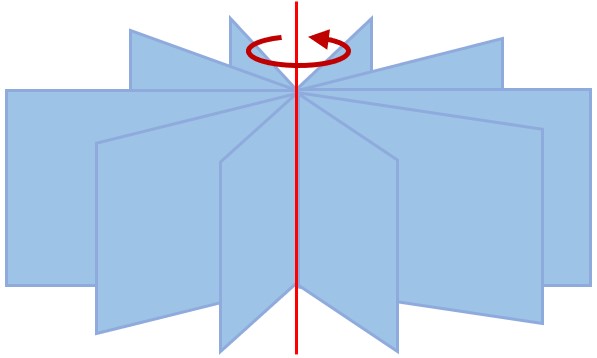
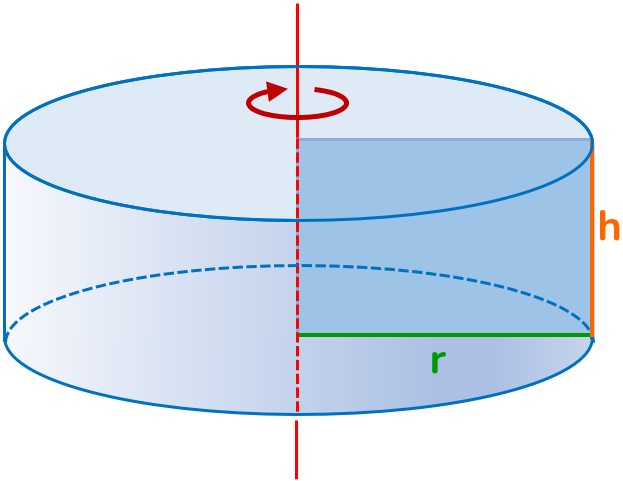
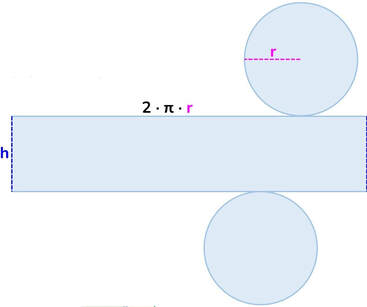
Solido → qualunque figura che occupa uno spazio tridimensionale, dotato quindi di un estensione in tre dimensioni diverse e tra loro perpendicolari.
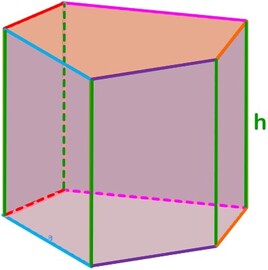
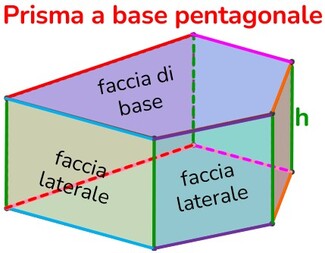
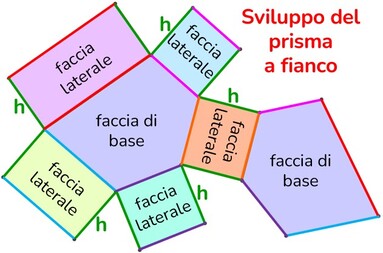
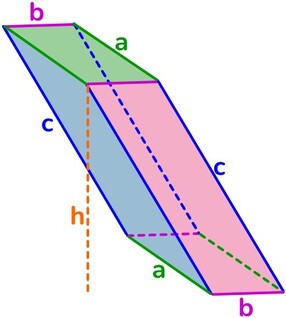
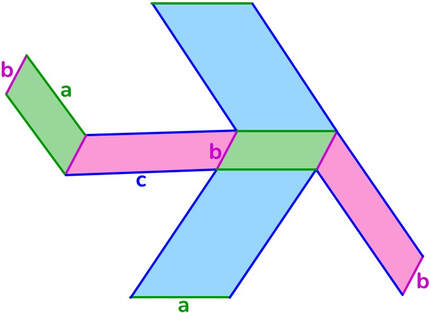
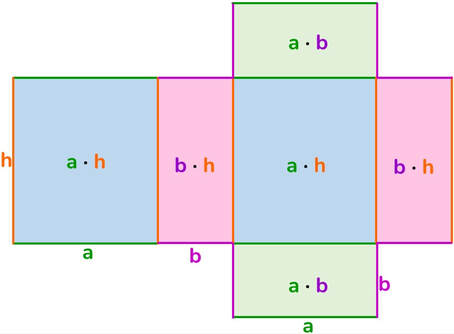
Poliedro → solido la cui superficie esterna è delimitata da poligoni.
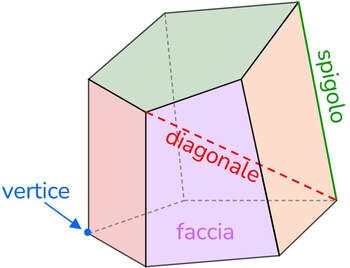
Faccia → ciascuno dei poligoni che formano la superficie del poliedro.
Spigolo → sono i lati dei poligoni che costituiscono le facce del poliedro.
Vertice → ciascuno dei punti nei quali convergono le facce, sono così gli estremi di ciascuno spigolo.
Diagonale → qualunque segmento che ha come estremi due vertici non appartenenti alla stessa faccia.
Poliedro → solido la cui superficie esterna è delimitata da poligoni.
Faccia → ciascuno dei poligoni che formano la superficie del poliedro.
Spigolo → sono i lati dei poligoni che costituiscono le facce del poliedro.
Vertice → ciascuno dei punti nei quali convergono le facce, sono così gli estremi di ciascuno spigolo.
Diagonale → qualunque segmento che ha come estremi due vertici non appartenenti alla stessa faccia.
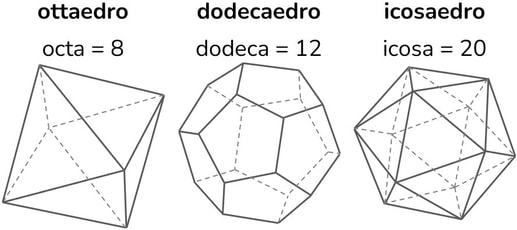
Poliedri regolari
I poliedri (più facce) regolari sono solo 5 e vengono chiamati anche solidi platonici.
Queste le caratteristiche dei solidi platonici:
Queste le caratteristiche dei solidi platonici:
- le loro facce sono poligoni regolari tutti congruenti tra loro;
- in ogni vertice converge sempre lo stesso numero di facce.
In ogni poliedro, sia esso concavo o convesso, il numero delle facce, dei vertici e degli spigoli sono in relazione tra loro.
Conoscendo la quantità di due di loro è possibile conoscere il terzo incognito.
Conoscendo la quantità di due di loro è possibile conoscere il terzo incognito.
La relazione di Eulero dice che:
numero delle facce + numero dei vertici = numero degli spigoli + 2
da cui:
f = s + 2 – v v = s + 2 – f s = f + v – 2
numero delle facce + numero dei vertici = numero degli spigoli + 2
da cui:
f = s + 2 – v v = s + 2 – f s = f + v – 2
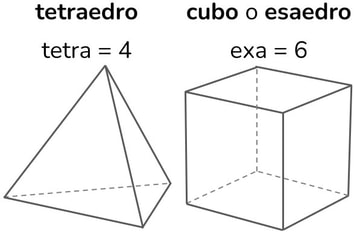
Prendiamo ad esempio il tetraedro rappresentato sopra, esso ha 4 facce, 4 vertici e 6 spigoli.
Vediamo se è rispettata la relazione di Eulero: f + v = s + 2 → 4 + 4 = 6 + 2 → 8 = 8
Vediamo se è rispettata la relazione di Eulero: f + v = s + 2 → 4 + 4 = 6 + 2 → 8 = 8
Prendiamo ad esempio il cubo rappresentato sopra, esso ha 6 facce, 8 vertici e 12 spigoli.
Vediamo se è rispettata la relazione di Eulero: f + v = s + 2 → 6 + 8 = 12 + 2 → 14 = 14
Vediamo se è rispettata la relazione di Eulero: f + v = s + 2 → 6 + 8 = 12 + 2 → 14 = 14