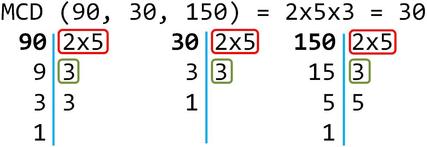MCD
Massimo Comune Divisore
Il più grande numero che divide senza dare resto tutti i numeri

In "matematichese" si definisce come:
il più grande divisore comune a due o più numeri. 

Usa la tavola dei divisori, segui l’esempio e poi prova tu.
Trova i divisori e scrivili dentro delle parentesi graffe.​

MCD (45; 30)
Divisori di 45 = {1, 3, 5, 9, 15, 45}
Divisori di 30 = {1, 3, 5, 15, 30}

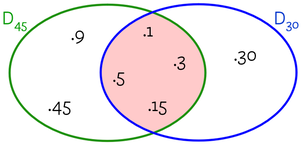
Nell’intersezione (parte in rosa) metti i divisori comuni a 45 e 30 = {1, 3, 5, 15}

Il MCD è il divisore comune più grande.
MCD (45; 30) = 15

---

È importante ricordare che il MCD:

• non è mai più grande della differenza dei due; 
  MCD (14, 16) = 2    16 - 14 = 2    la differenza è uguale al MCD; 
  MCD (14, 18) = 2    18 - 14 = 4    la differenza è maggiore del MCD;
• non è mai più grande più piccolo dei numeri presenti;
  MCD (158; 14; 2800) è sicuramente minore o uguale a 14.
• Se due numeri sono uno multiplo dell’altro, il MCD è il più piccolo dei due
  MCD (16; 48) = 16
• ​è uguale a 2 quando i numeri sono consecutivi pari 
  MCD (26; 28) = 2
  MCD (1854; 1856) = 2.

---

Il MCD tra due o più numeri è uguale a 1 quando:

• il più grande tra tutti è un numero primo
  MCD (25, 32 e 97) = 1 perché 97 è un numero primo
  infatti
  D (25) = 1, 5, 25
  D (32) = 1, 2, 4, 8, 16, 32
  D (97) = 1, 97​

• i numeri sono primi tra loro (non hanno nessun divisore in comune escluso l'1)
  MCD (14, 16, 27) = 1
  infatti
  D (14) = 1, 2, 7, 14
  D (16) = 1, 2, 4, 8, 16
  D (27) = 1, 3, 9, 27
  non esiste nessun divisore comune contemporaneamente ai tre numeri.

• i numeri sono consecutivi   
  MCD (25; 26) = 1
  infatti
  D (25) = 1, 5, 25
  D (26) = 1, 2, 13, 26

• quando i numeri sono consecutivi dispari 
  MCD (33, 35) = 1
  infatti
  D (33) = 1, 3, 11, 33
  D (35) = 1, 5, 7, 35

---

Calcolare il MCD di due o più numeri
​con le scomposizioni in fattori primi

Il MCD si trova prendendo ogni fattore comune a tutti i numeri, preso una sola volta abbinando il più piccolo esponente presente.

Vediamo passo a passo come si opera:

1. fare la scomposizione in fattori primi;
2. scrivere ciascun numero come prodotto di potenze le cui basi sono numeri primi;
3. prendere ogni base comune a tutti, solo una volta;
4. mettere a ciascuna base l'esponente più piccolo presente;
5. risolvere le singole potenze, poi moltiplicare i fattori.

---

Calcolo del MCD tramite il metodo delle sottrazioni successive

Un altro metodo, sicuramente meno conosciuto, e che non richiede la conoscenza delle tabelline, è quello delle sottrazioni successive.

Per usare questo metodo si opera in questo modo:

1. Calcolo la differenza tra i due numeri dei quali vorrei il MCD;
2. escludo il più grande, tolgo il più piccolo al medio; 
3. continuo in questo modo fino a quando i due numeri più piccoli non sono uguali.

MCD (45, 18) =

Calcolo la differenza tra i due numeri
Faccio la differenze tra i due numeri minori
Continuo a calcolare la differenza fino a quando due numeri minori non sono uguali 

45 - 18 = 27
27 - ​18 = 9
​18 - 9 = 9

Il Massimo Comune Divisore tra 45 e 18 è = 9

---

MCD con l'algoritmo di Euclide

L'uso di questo metodo non richiede scomposizioni o conoscenze di divisibilità. 

MCD (168, 63) =

Quante volte il minore sta nel maggiore?

168 : 63 = 2   R = 42

Prendo in considerazione i due numeri minori, 63 e 42, quante volte il 42 sta nel 63?

63 : 42 = 1     R = 21

Ripeto il meccanismo fino a quando il resto è zero.
Il 21 è il Massimo Comune Divisore tra 168 e 63

42 : 21 = 2     R = 0

---

Calcolo del MCD di due o più numeri utilizzando un'unica tabella

Con questo metodo, può essere scelto come divisore anche un numero che non è primo, la cosa importante è che sia comune a TUTTI i numeri. 

MCD (450, 660, 720) =

Scrivo i numeri iniziali	#1	#2	#3	Divisori comuni a tutti
Posso dividere tutti per 10 perché tutti i numeri finiscono con uno zero	450	660	720	10
Divido 45, 66 e 72 per 3	45	66	72	3
Poiché non capisco se posso dividerli per una stessa quantità, li scompongo in fattori primi	15	22	24	Nessun fattore comune a tutti
15, 22 e 24 non hanno un divisore comune a tutti.	3·5	2·11	3·2·2·2	MCD=10·3=30

---

Il Massimo Comune Divisore nei problemi

Ogni volta che dovrai distribuire delle quantità di modo da formare gruppi che hanno la stessa quantità di ciascun tipo di oggetto devi calcolare il MCD tra queste quantità.
In questo caso il MCD rappresenta la più grande quantità dei gruppi (vassoi, vasi, sacchetti, ..) che puoi formare.
Comporre vassoi con la stessa quantità di pizzette, panzerotti e pasticcini.
Comporre vasi di fiori aventi ciascuno la stessa quantità di rose, margherite e tulipani

In tutti questi casi devi calcolare il MCD tra le quantità totali di ciascuno.

Il MCD rappresenta la quantità totale dei gruppi.
Il primo numero : MCD → la quantità del primo oggetto in ciascun gruppo
Il secondo numero : MCD → la quantità del secondo oggetto in ciascun gruppo
​Il terzo numero : MCD → la quantità del terzo oggetto in ciascun gruppo
​...

---

Il Massimo Comune Divisore e il minimo comune multiplo

Verifica se i tuoi calcoli sono giusti, inserisci i numeri e poi premi il pulsante calcola.

Calcolo M.C.D. e m.c.m.

Attenzione: le caselle vanno riempite nell'ordine dato: 1°, 2°, 3°, 4°, altrimenti i risultati potrebbero essere sbagliati!

---

Contatore inserito in data 21 aprile 2021

---