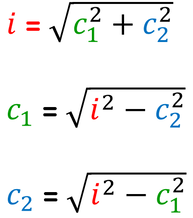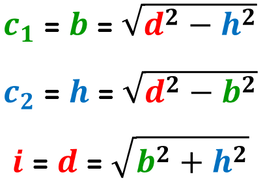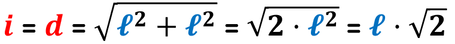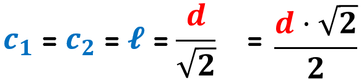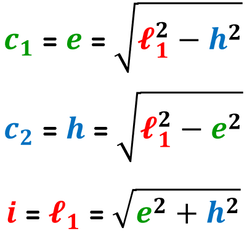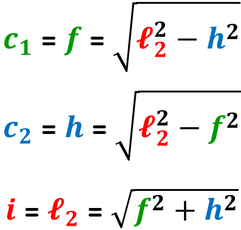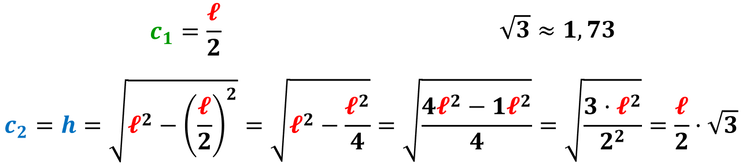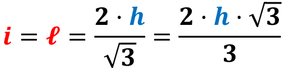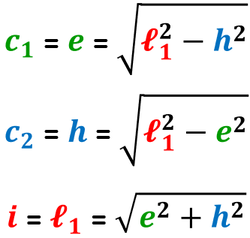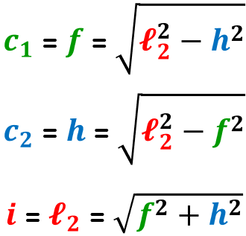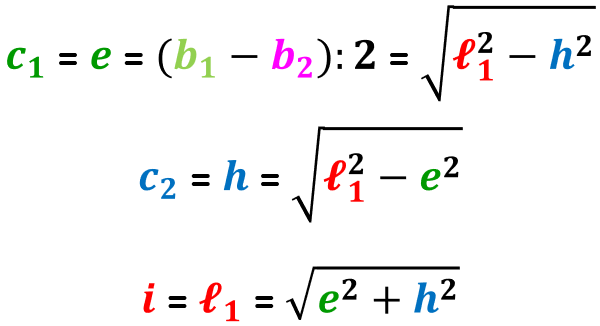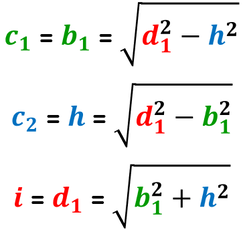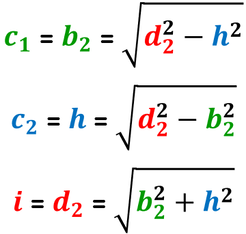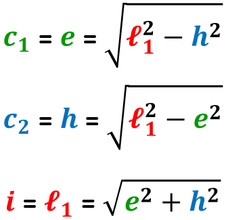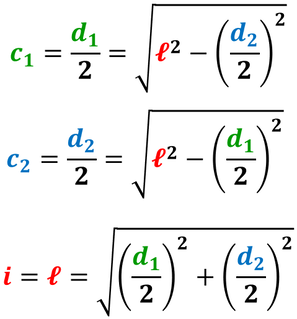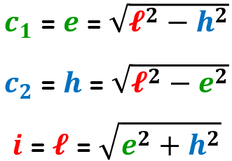DOVE PUÒ ESSERE APPLICATO IL TEOREMA DI PITAGORA?
Alcune volte i problemi di geometria ci richiedono di trovare la misura di un lato o di un elemento interno alla figura geometrica (come l'altezza relativa ad un lato, una diagonale, ...) e le formule inverse dell'area e del perimetro non riescono a venirci incontro.
In ciascuna figura ho messo in evidenza, colorandoli di giallo, i diversi triangoli rettangoli che possiamo disegnare e le rispettive formule per poterne calcolare la misura dei lati.
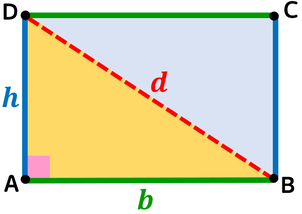
Rettangolo
Il rettangolo ha gli angoli interni tutti di 90°, per cui, ciascuna diagonale lo divide in due triangoli rettangoli.
Nel rettangolo:
Nel rettangolo:
- l'ipotenusa è la diagonale;
- i cateti sono i lati (base e altezza).
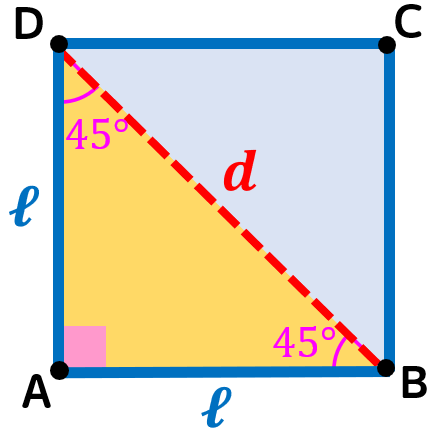
Quadrato
Triangolo rettangolo isoscele
Anche il quadrato, come il rettangolo, ha gli angoli interni uguali a 90°: ciascuna diagonale divide così il quadrato in due triangoli rettangoli isosceli.
Quando hai di fronte a te un triangolo rettangolo isoscele ricorda che esso ha due angoli di 45°.
Se un triangolo rettangolo ha gli angoli acuti congruenti a 45° si tratta metà quadrato.
Quando hai di fronte a te un triangolo rettangolo isoscele ricorda che esso ha due angoli di 45°.
Se un triangolo rettangolo ha gli angoli acuti congruenti a 45° si tratta metà quadrato.
Per conoscere la misura della diagonale applichiamo il teorema di Pitagora, mentre per conoscere la misura del lato, a partire dalla misura della diagonale, possiamo invertire la formula usata per trovare la diagonale.
Triangolo scaleno
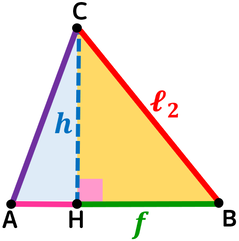
L'altezza in un triangolo è quel segmento che, condotto da un vertice, raggiunge il lato opposto, o il suo prolungamento, perpendicolarmente (cioè formando angoli retti).
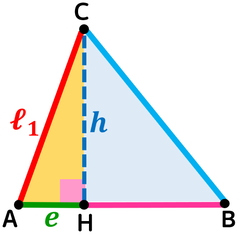
Se il triangolo è acutangolo, ciascuna altezza divide il triangolo stesso in due triangoli rettangoli, e l'altezza divide così il lato opposto, che diventa base, in due parti: ciascuna parte è la proiezione degli altri due lati.
Le proiezioni dei lati obliqui sulla base nel triangolo sotto corrispondono ai segmenti e e f.
I triangoli rettangoli sono così formati:
Se il triangolo è acutangolo, ciascuna altezza divide il triangolo stesso in due triangoli rettangoli, e l'altezza divide così il lato opposto, che diventa base, in due parti: ciascuna parte è la proiezione degli altri due lati.
Le proiezioni dei lati obliqui sulla base nel triangolo sotto corrispondono ai segmenti e e f.
I triangoli rettangoli sono così formati:
- l'ipotenusa è il lato obliquo che sto considerando;
- il primo cateto è la proiezione dello stesso lato obliquo sulla base;
- il secondo cateto è l'altezza relativa alla base.
Triangolo isoscele
Ha due lati congruenti chiamati lati obliqui.
Il lato diverso viene chiamato base.
L’altezza relativa alla base è bisettrice, mediana e asse, dunque divide il triangolo in due triangoli rettangoli tra loro congruenti.
Il lato diverso viene chiamato base.
L’altezza relativa alla base è bisettrice, mediana e asse, dunque divide il triangolo in due triangoli rettangoli tra loro congruenti.
I triangoli rettangoli sono così formati:
- l'ipotenusa è il lato obliquo;
- il primo cateto è la proiezione del lato obliquo sulla base
e corrisponde a metà base; - il secondo cateto è l'altezza relativa alla base.
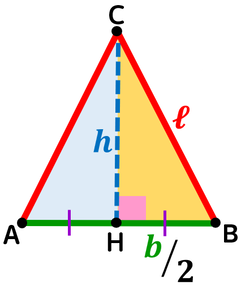
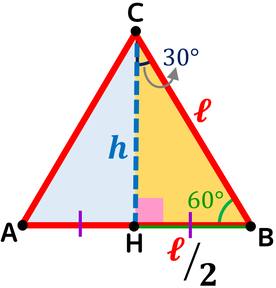
Triangolo equilatero
Triangolo rettangolo con angoli 30° e 60°
Un triangolo equilatero ha anche tutti gli angoli tra loro congruenti a 60°.
L'altezza relativa a qualunque lato divide il triangolo in due triangoli rettangoli congruenti: ciascuno di essi è un triangolo rettangolo avente gli angoli acuti uguali a 30° e a 60° e sono sempre metà triangolo equilatero.
Dunque un triangolo rettangolo con angoli acuti di 30° e 60° può essere considerato metà triangolo equilatero.
L'altezza relativa a qualunque lato divide il triangolo in due triangoli rettangoli congruenti: ciascuno di essi è un triangolo rettangolo avente gli angoli acuti uguali a 30° e a 60° e sono sempre metà triangolo equilatero.
Dunque un triangolo rettangolo con angoli acuti di 30° e 60° può essere considerato metà triangolo equilatero.
Questo particolare triangolo rettangolo ha come:
- ipotenusa il lato obliquo;
- primo cateto la metà del lato obliquo;
- secondo cateto è l'altezza relativa alla base.
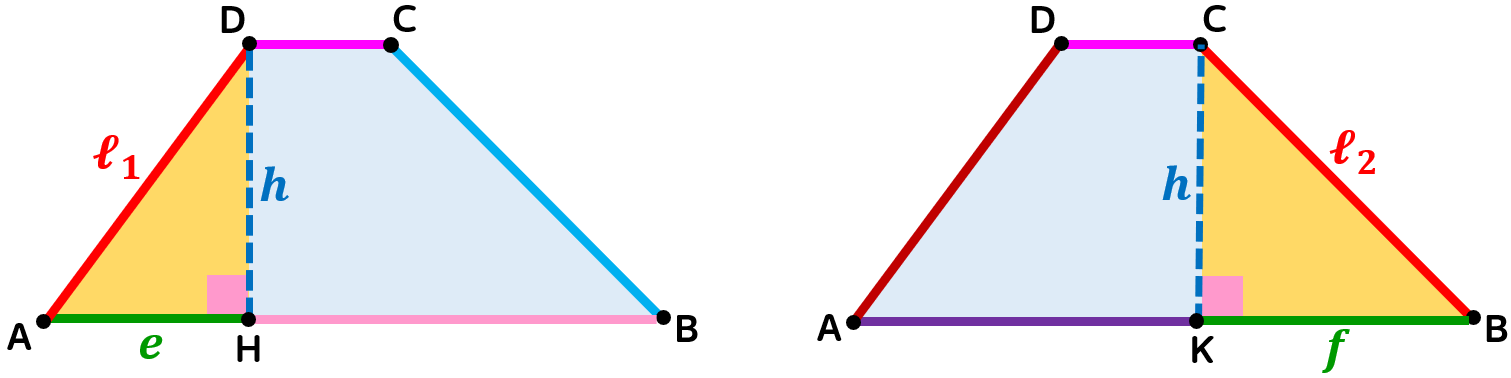
Trapezio scaleno
Le altezze in un trapezio scaleno condotte dagli estremi della base minore dividono la figura in tre parti: due triangoli rettangoli e un rettangolo.
Possiamo così affermare che in ciascun triangolo rettangolo:
Possiamo così affermare che in ciascun triangolo rettangolo:
- il lato obliquo è l'ipotenusa;
- la proiezione dello stesso lato obliquo sulla base maggiore è il primo cateto;
- l'altezza è il secondo cateto.
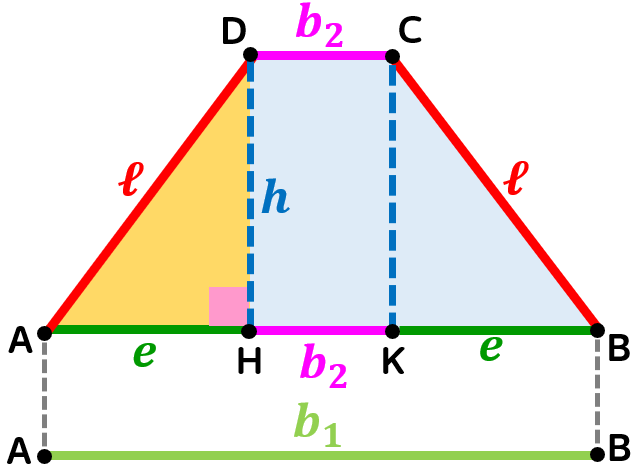
Trapezio isoscele
Il trapezio isoscele è un trapezio avente come lati obliqui due lati tra loro congruenti.
Le altezze condotte dagli estremi della base minore dividono il trapezio in tre parti: due triangoli rettangoli tra loro congruenti e un rettangolo (che talvolta può essere un quadrato quando la base minore e l'altezza hanno la stessa lunghezza.
Possiamo così affermare che in ciascun triangolo rettangolo:
Le altezze condotte dagli estremi della base minore dividono il trapezio in tre parti: due triangoli rettangoli tra loro congruenti e un rettangolo (che talvolta può essere un quadrato quando la base minore e l'altezza hanno la stessa lunghezza.
Possiamo così affermare che in ciascun triangolo rettangolo:
- il lato obliquo è l'ipotenusa;
- la proiezione del lato obliquo sulla base maggiore è il primo cateto;
- l'altezza è il secondo cateto.
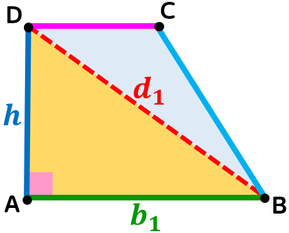
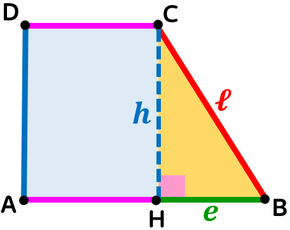
Trapezio rettangolo
Nel trapezio rettangolo è possibile individuare tre diversi triangoli rettangoli.
CASO 1 - LA DIAGONALE MAGGIORE
Nel triangolo rettangolo individuato dalla diagonale maggiore:
- la diagonale maggiore è l'ipotenusa;
- la base maggiore è il primo cateto;
- l'altezza è il secondo cateto.
CASO 2 - LA DIAGONALE MINORE
Nel triangolo rettangolo individuato dalla diagonale maggiore:
- la diagonale minore è l'ipotenusa;
- la base minore è il primo cateto;
- l'altezza è il secondo cateto.
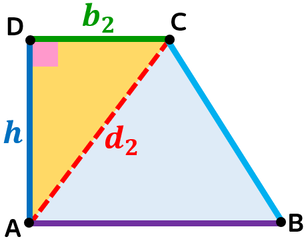
CASO 3 - L'ALTEZZA CONDOTTA DALL'ALTRO ESTREMO DELLA BASE MINORE
Nel triangolo rettangolo individuato dall'altezza condotta dall'altro estremo della base minore:
- il lato obliquo è l'ipotenusa;
- la proiezione del lato obliquo sulla base maggiore è il primo cateto;
- l'altezza è il secondo cateto.
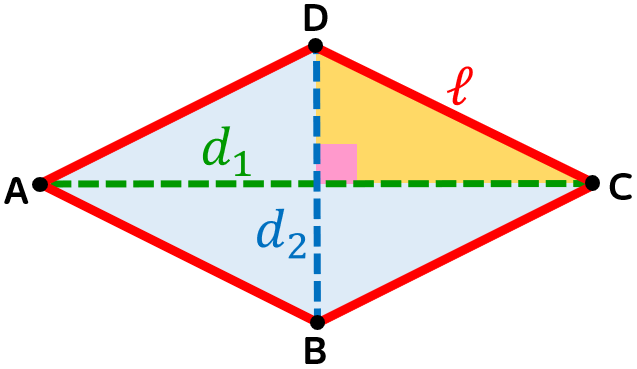
Rombo
Ciascun triangolo rettangolo ha come:
- ipotenusa il lato obliquo;
- primo cateto la metà di una diagonale;
- secondo cateto la metà dell'altra diagonale.
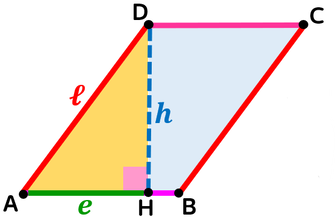
Parallelogramma
L'altezza interna condotta da un estremo del lato opposto divide il parallelogramma in due parti, una di queste è un triangolo rettangolo.
In questo triangolo rettangolo:
- il lato obliquo è l'ipotenusa;
- la proiezione del lato obliquo sul lato consecutivo è il primo cateto;
- l'altezza è il secondo cateto.
Contatore messo in data 30 marzo 2021