Gli enti primitivi
Sono elementi della geometria dei quali non viene dimostrata la loro esistenza e le loro caratteristiche.
Gli enti primitivi sono: il punto, la retta e il piano.
Gli enti primitivi sono: il punto, la retta e il piano.
Il puntoÉ uno strumento astratto che, nonostante venga rappresentato, il punto non ha dimensioni.
Si indica con le lettere maiuscole dell'alfabeto (A, B, D, P, ...). Si utilizza per indicare:
|
Sposta il punto A nel piano cartesiano e osserva come variano le sue coordinate, oppure disegnane di nuovi utilizzando lo strumento punto.
|
|
I punti, nel piano cartesiano, sono indicati da una lettera maiuscola e da due numeri separati da una virgola e posti dentro una parentesi tonda.
I due numeri prendono il nome di coordinate del punto:
Nel disegno a fianco:
|
Muovi il punto A e vedi come cambiano le sue coordinate.
|
Per disegnare un punto nel piano cartesiano, conoscendo le sue coordinate, ricerca il primo numero sull'asse orizzontale (asse delle x o delle ascisse), ritrovato il numero vado sulla verticale in basso (se il secondo numero è negativo) o in alto (se il secondo numero non è preceduto da un segno o è positivo), fino a quando non si sarà raggiunta la linea orizzontale nella quale è indicato il secondo numero nell'asse verticale.
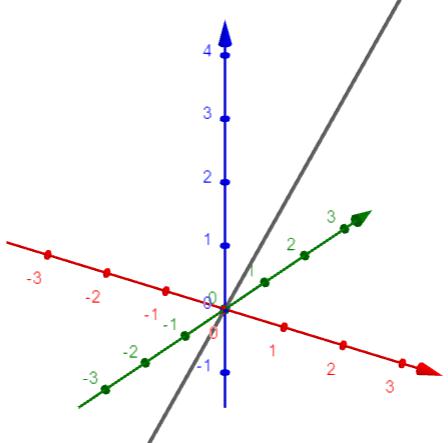
La rettaLa retta ha una sola dimensione: la lunghezza.
È composta da infiniti punti che guardano tutti nella stessa direzione. Non ha né inizio né fine, si dice così che è infinita. Le rette si rappresentano con le lettere minuscole dell'alfabeto (a, b, c, d, ...) o con due dei suoi punti (AB, KL, SR, ...). |
|
Muovi i punti A e B nel piano cartesiano e osserva come l'equazione implicita che la definisce muta. Prova a mettere A e B nella stessa verticale o nella stessa linea orizzontale, che cosa succede?
Le rette nel piano cartesiano sono identificate da una formula matematica nella quale compaiono la lettera x oppure la lettera y oppure sia la lettera x che quella y e sempre un numero, che può essere anche lo zero.
Puoi disegnare anche tu delle nuove rette utilizzando prima lo strumento punto per disegnare due punti, poi con lo strumento retta fai un click esattamente sui due punti che hai appena disegnato (sei sicuro di aver preso esattamente i punti quando il click sarà fatto quando il puntatore da freccia muta in manina).
Il pianoHa due sole dimensioni: la larghezza e la lunghezza.
Non ha uno spessore. Si estende infinitamente in entrambe le dimensioni. I piani si rappresentano con le lettere greche dell'alfabeto (α, β, γ, δ, ...). |
|
Gli enti fondamentali
Le semiretteSi chiama semiretta ciascuna delle due parti in cui è stata divisa una retta da uno dei suoi punti.
Il punto scelto viene chiamato origine delle due semirette. Una semiretta ha lunghezza infinita. Una semiretta se ha un inizio non ha una fine, oppure se ha una fine non ha un inizio. |
|
Nel piano cartesiano, disegnati due dei suoi punti, ricorda:
Sposta i punti A, B e C e vedi com'è modificata la formula matematica (equazione) che identifica la semiretta.
L'equazione della semiretta è identica all'equazione della retta che passa per i due punti considerati.
- la retta AB ha origine in A e passa per il punto B;
- la retta BA, come quella nel piano sopra, ha origine in B e passa per il punto A.
Sposta i punti A, B e C e vedi com'è modificata la formula matematica (equazione) che identifica la semiretta.
L'equazione della semiretta è identica all'equazione della retta che passa per i due punti considerati.
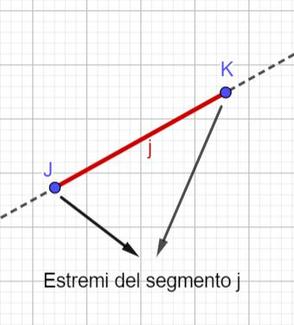
I segmentiSi chiama segmento quella parte di retta delimitata da due dei suoi punti non coincidenti.
I punti che delimitano il segmento si chiamano estremi del segmento. Ogni segmento è formato da infiniti punti (con una lente puoi sempre ingrandire lo spazio tra due punti e vedere che ne puoi sempre disegnare altri), ma possiede sia un inizio che una fine. |
|
Nel piano cartesiano un segmento può essere identificato:
- tramite i suoi punti estremi (AB, DK, ...);
- tramite una lettera minuscola dell'alfabeto (a, b, k, r, ...).
Sul piano cartesiano sopra, prova a disegnare due punti e poi il segmento usando lo strumento appropriato.
|
Segmenti consecutivi
|
Segmenti adiacenti
|
|
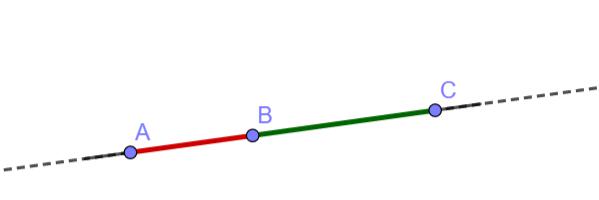
Due segmenti si dicono consecutivi
quando hanno un estremo in comune (è come se i due segmenti si prendessero per mano). |
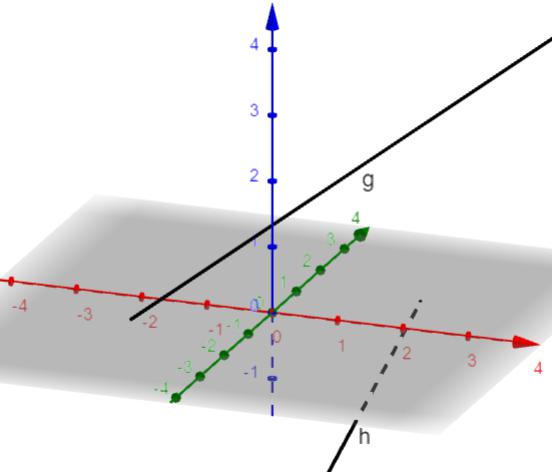
Due segmenti si dicono adiacenti
quando sono consecutivi e giacciono su parti opposte di una stessa retta (i due segmenti sono presi per mano a formare un unico segmento). |
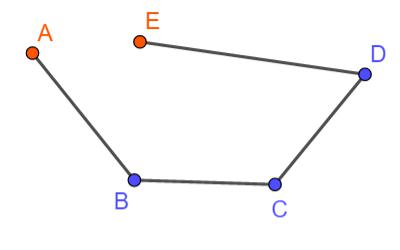
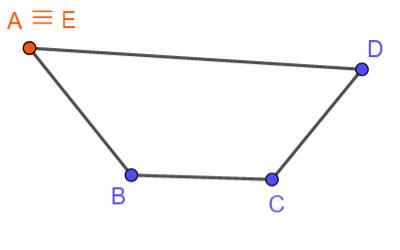
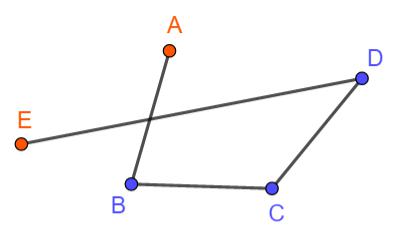
Le poligonali
Si chiama poligonale una catena di segmenti dove un segmento è consecutivo ad un altro segmento (è come se i segmenti si prendessero per mano l'un l'altro).
|
Poligonale aperta
|
Poligonale chiusa
|
Poligonale intrecciata
|
Impariamo qualche strumento in più:
- segmento → puoi usare due metodi: 1) disegna due punti e poi con lo strumento segmento fai un click su entrambi; 2) fai click sul piano cartesiano esattamente nei punti che saranno gli estremi del tuo segmento;
- spezzata aperta → disegna tanti punti che saranno gli estremi dei diversi segmenti, ogni segmento avrà in comune un estremo con un altro segmento, fatta eccezione il primo e l'ultimo;
- poligono → fai click sul piano cartesiano, tante volte quanti sono i vertici del poligono, infine chiudi il poligono facendo un click sul primo punto del poligono appena disegnato;
- poligono regolare → fai due click sul piano cartesiano, ricordando che la loro distanza sarà il lato del poligono, al secondo click si aprirà una finestra nella quale indicare il numero dei lati del poligono regolare che si vuole rappresentare.
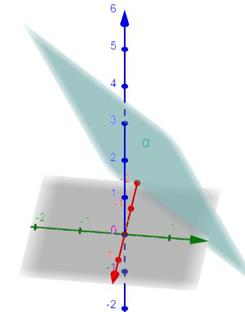
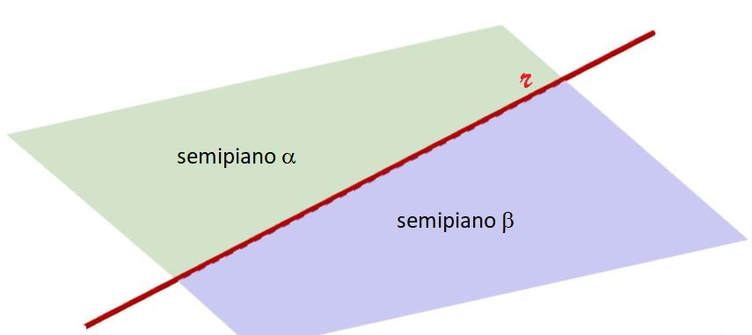
I semipiani
Si chiama semipiano ciascuna delle due parti di piano delimitata da una sua retta.
Gli angoli
Clicca sul titolo "angoli" per andare sulla pagina dedicata.