IL PIANO CARTESIANO

Caratteristiche

Quando dobbiamo disporre i numeri in modo ordinato utilizziamo le rette orientate.
Nelle rette orientate, fissato un punto detto origine della retta, al quale diamo valore 0, e fissato un orientamento, generalmente verso destra o verso l'alto, diremo:
- se la retta è orizzontale, che

• i numeri sono posti dal più piccolo al più grande andando da sinistra verso destra;
• i numeri alla destra dello zero sono positivi, quindi maggiori di zero;
• i numeri alla sinistra dello zero sono negativi, quindi minori di zero.

-  se la retta è verticale che

• i numeri sono posti dal più piccolo al più grande andando dal basso verso l'alto (come i piani di un ascensore);
• i numeri sotto lo zero sono negativi, quindi minori di zero;
• i numeri sopra lo zero sono positivi, quindi maggiori di zero.

Se disegniamo le due rette, quella orizzontale e quella verticale, di modo che abbiano in comune il punto origine, abbiamo disegnato un piano cartesiano.

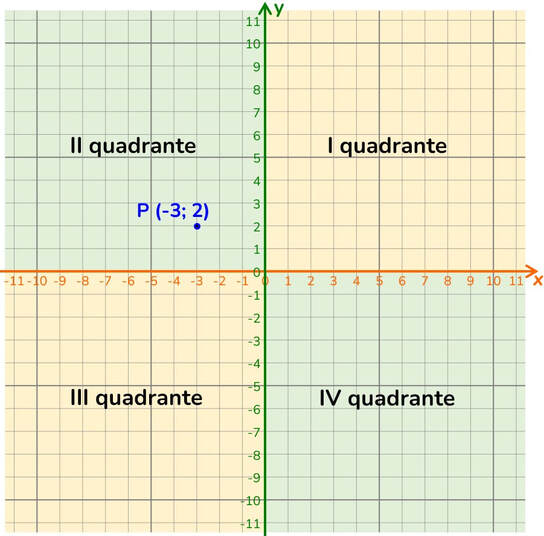
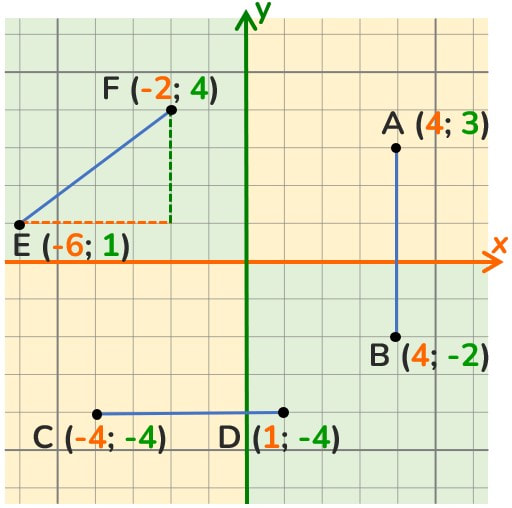
Il piano cartesiano è un piano nel quale sono state disegnate due rette orientate ortogonali tra loro (una orizzontale e l’altra verticale), nelle quali al punto di intersezione tra esse è dato come valore zero.
Punto di intersezione tra le rette → origine del piano cartesiano
Retta orizzontale → asse delle ascisse o asse delle x
Retta verticale → asse delle ordinate o asse delle y
​
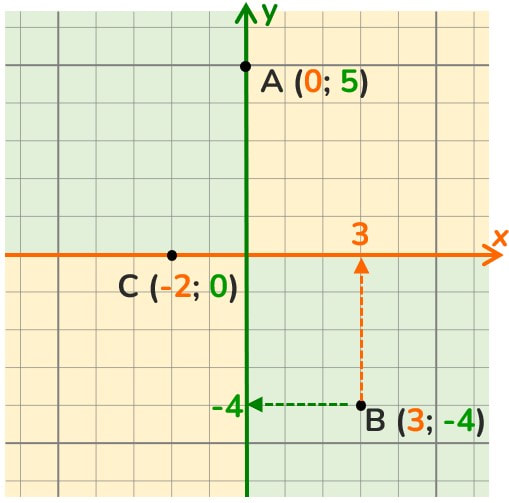
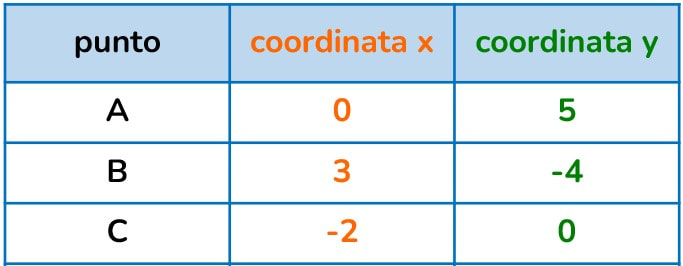
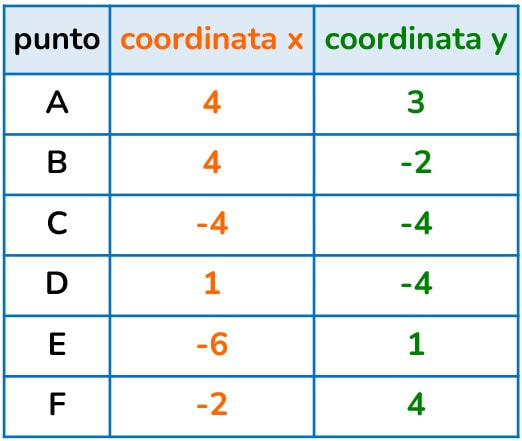
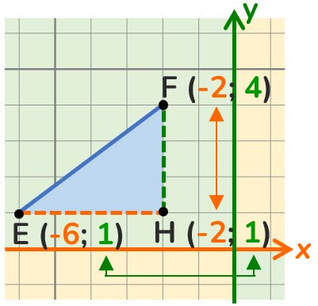
​Qualunque punto disegnato nel piano cartesiano sarà contraddistinto da due numeri che ne danno la loro collocazione univoca.

Il punto e la sua proiezione su una retta

Il punto è il primo ente primitivo.
Il punto non ha dimensioni, è in pratica uno strumento che ci permette di dare la posizione di diversi oggetti, ad esempio gli estremi di un segmento, i vertici di un poligono, … ​

Nel disegno a destra dal punto P ho tracciato le perpendicolari alle due rette r e s, che individuano due punti di intersezione:

• Pr → proiezione del punto P sulla retta r
• Ps → proiezione del punto P sulla retta s

Proiezione di un punto su una retta → punto individuato in una retta conducendo da un punto esterno la sua perpendicolare.

Coordinate di un punto nel piano cartesiano

Si chiamano coordinate del punto la coppia di numeri formata dal valore delle ascisse e da quello delle ordinate:

nome del punto (ascissa del punto; ordinata del punto)

B (3; -4)

Se il punto si trova sull’asse x → le coordinate del punto avranno ascissa uguale al numero sull’asse x e ordinata uguale a zero → C (-2; 0). 

Se il punto si trova sull’asse y → le coordinate del punto avranno ascissa uguale a zero e ordinata uguale al numero identificato nell’asse → A (0; 5).

Chiameremo xA la coordinata x del punto A.
Chiameremo yA la coordinata y del punto A.
Quando avrai a che fare con tanti punti e dovrai lavorare con le loro coordinate, costruisci una tabella come quella a fianco.

I segmenti nel piano cartesiano e la loro lunghezza

Calcolare la distanza tra due punti distinti A e B vuol dire calcolare la lunghezza del segmento che ha come estremi i punti A e B.

Se il segmento è parallelo (o perpendicolare) ad un asse, calcolarne la lunghezza è davvero semplice: calcola la differenza tra le coordinate x o y che sono diverse tra loro.

Costruiamo una tabella delle coordinate dei punti di modo da avere tutto sott’occhio e non confonderti.

La distanza tra i punti A e B, come pure il segmento che ha per estremi i punti A e B, li indicheremo con AB. Dall’analisi delle sue coordinate possiamo vedere che le coordinate x di entrambi i punti sono uguali: xA = xB = 4 (infatti AB è parallelo all’asse y); invece le coordinate y dei due punti sono diverse, in questo caso avremo: 

(come già visto in algebra, le due barrette verticali che racchiudono le coordinate y di A e B, ci danno l’indicazione che a prescindere dal segno della sottrazione a noi interessa solo il numero, anche perché una lunghezza non può mai essere negativa).

Il segmento BC è invece parallelo all’asse x, infatti i valori delle coordinate y dei due punti sono uguali: yC = yD = – 4

Se il segmento non è parallelo a nessuno degli assi cartesiani diremo che il segmento è obliquo. Nei segmenti obliqui agli assi le coordinate x dei due punti sono diverse tra loro, come pure saranno diverse le rispettive coordinate y. ​

Vediamo nel dettaglio il segmento rappresentato nel piano cartesiano sopra:

Due segmenti, uno parallelo all’asse x e un altro parallelo all’asse y sono stati condotti dai vertici E e F fino a farli incontrare.

Delimitano così un triangolo rettangolo nel quale:

• EH → primo cateto (parallelo all’asse x) → EH = |xE – xH|
• FH → secondo cateto (parallelo all’asse y) → FH = |yF – yH|
• EF → ipotenusa (il segmento del quale dobbiamo trovare la lunghezza)

xH = xF = -2 e yH = yE = 1

Se di un triangolo rettangolo conosciamo la lunghezza dei suoi cateti allora possiamo conoscere la lunghezza dell’ipotenusa applicando il teorema di Pitagora:

Punto medio tra due punti ​o punto medio di un segmento

Punto medio → quel punto che divide esattamente a metà un segmento o la distanza tra due punti.
Dividere a metà → tagliare in due parti esattamente congruenti (uguali tra loro).

Chiameremo:

• MAB → il punto medio del segmento che ha per estremi i punti A e B
• xM → coordinata x del punto medio
• yM → coordinata y del punto medio

Condotti dagli estremi due segmenti paralleli agli assi si individua un triangolo rettangolo nel quale il segmento è l’ipotenusa, trovare il punto medio del segmento vuol dire trovare il punto medio di ciascuno dei due cateti:

La mediana

La mediana è quel segmento che, in un triangolo, ha come estremi un vertice e il punto medio del lato opposto.
​
Occorre quindi:
- trovare il punto medio del lato del triangolo considerato;
- calcolare la distanza, e di conseguenza la lunghezza, tra il punto medio e il vertice opposto al lato.

Pagina rivista il 6 settembre 2022