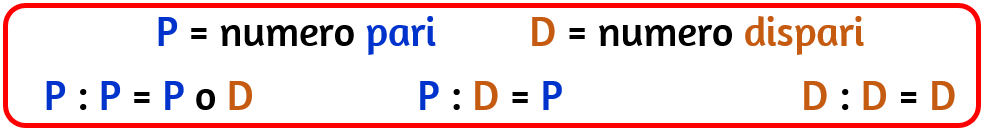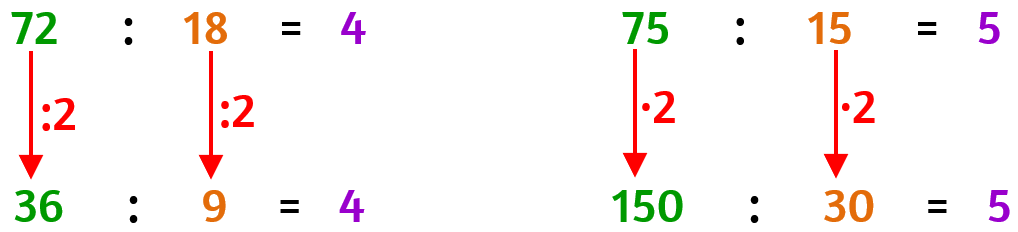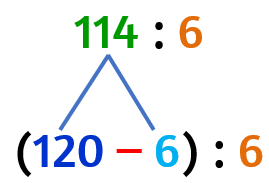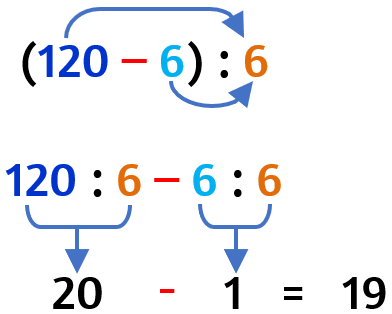LA DIVISIONELa divisione è l’operazione che, dati due numeri qualsiasi in un dato ordine, detti dividendo e divisore, ne associa un terzo, detto quoto* o quoziente* (risultato in N e Q), ottenuto raggruppando il dividendo in tante parti quante ne richiede il divisore oppure contando quante parti si possono ottenere, composte da tante unità quante ne indica il divisore.
|
QUOTO → il risultato di una divisione esatta, una divisione che non dà resto
QUOZIENTE → il risultato di una qualsiasi divisione
Fare una divisione vuol dire, dunque, separare una certa quantità (dividendo) in gruppi tutti composti allo stesso modo e quindi formati da un’altra quantità (divisore).
Il risultato della divisione (quoziente) è la quantità dei gruppi che ho formato.
Sulla retta dei numeri:
-il dividendo → la quantità dalla quale si parte
-il divisore → la lunghezza di ciascun salto
-il quoziente → la quantità totale dei salti
Il risultato della divisione (quoziente) è la quantità dei gruppi che ho formato.
Sulla retta dei numeri:
-il dividendo → la quantità dalla quale si parte
-il divisore → la lunghezza di ciascun salto
-il quoziente → la quantità totale dei salti
Il risultato della divisione risponde alla domanda:
quante volte il divisore è contenuto nel dividendo?
Se ci riferiamo all’esempio: quante volte il 3 è contenuto nel 15? 5 volte
quante volte il divisore è contenuto nel dividendo?
Se ci riferiamo all’esempio: quante volte il 3 è contenuto nel 15? 5 volte
La divisione esatta (quella che non dà resto) è l’operazione inversa della moltiplicazione tra numeri naturali. Sono definite divisioni approssimate quelle che danno un resto, cioè il cui quoziente non è un numero naturale ma un numero decimale.
Attenzione:
il resto della divisione deve essere sempre minore del divisore.
il resto della divisione deve essere sempre minore del divisore.
Se dividiamo tra loro due numeri naturali NON otteniamo sempre un numero naturale:
NON tutte le divisioni sono possibili (il risultato di una divisione è spesso un numero decimale) e per questo si dice che la divisione non è interna all'insieme dei numeri naturali.
NON tutte le divisioni sono possibili (il risultato di una divisione è spesso un numero decimale) e per questo si dice che la divisione non è interna all'insieme dei numeri naturali.
Lo zero e l'1 nella divisione
Nessun numero può essere diviso per zero.
Chiedersi quante volte lo zero è contenuto in una qualunque quantità non ha significato.
Chiedersi quante volte lo zero è contenuto in una qualunque quantità non ha significato.
15 : 0 = impossibile
0 : 0 = indeterminata
0 : 0 = indeterminata
Ma se lo zero occupa la posizione del dividendo e il divisore è diverso da zero, il risultato è zero.
0 : 15 = 0
Il numero uno è elemento neutro nella divisione solo se occupa la posizione del divisore: qualunque numero diviso 1 da come risultato il numero stesso
13 : 1 = 13
Numeri pari e numeri dispari nella divisione
In una divisione esatta:
- un numero pari diviso un numero pari darà come risultato un numero pari, 12 : 2 = 6, o un numero dispari, 12 : 4 = 3;
- un numero pari diviso un numero dispari darà sempre un numero pari;
- un numero dispari diviso un numero dispari darà sempre un numero dispari.
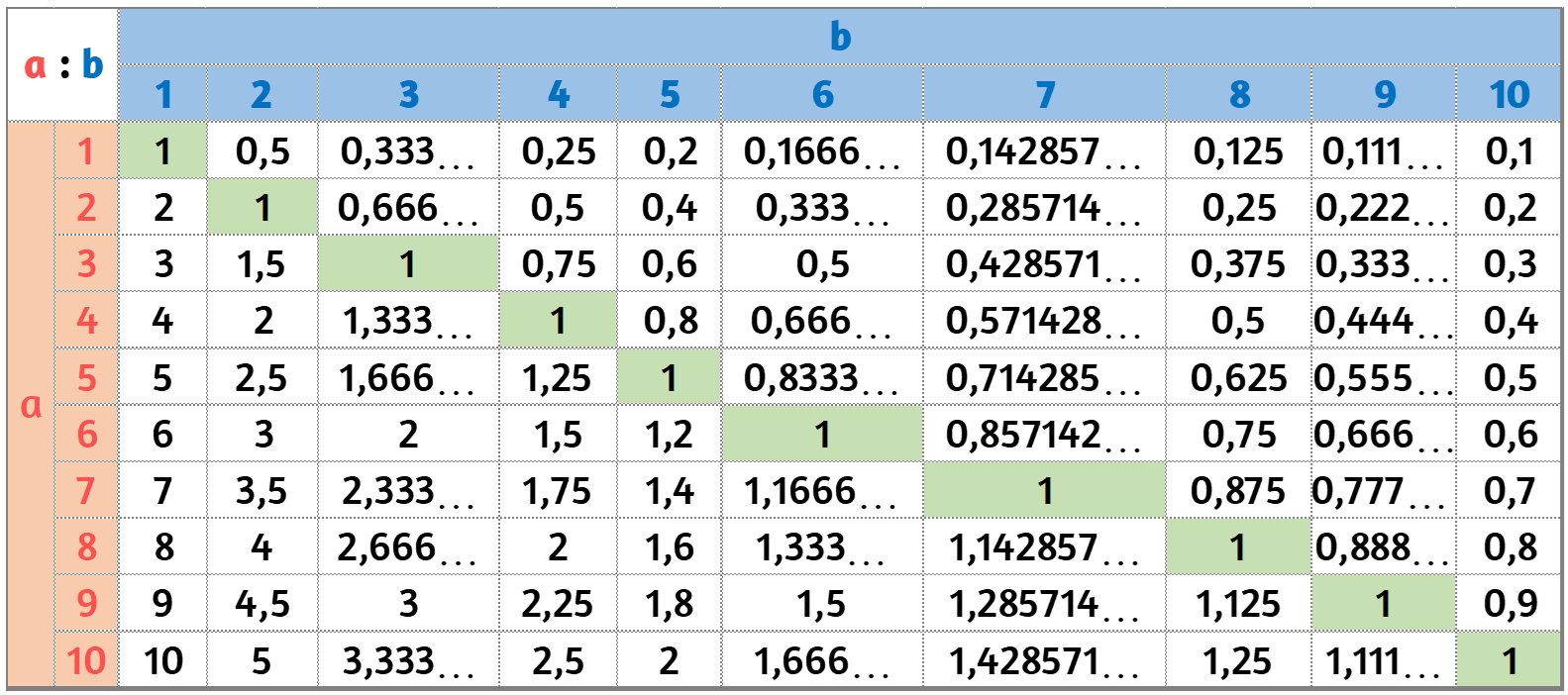
Tavola della divisione
Nota bene: al di sotto della diagonale verde i quozienti sono maggiori di uno (> 1) al di sopra della diagonale, i quozienti sono minori di uno (< 1).
COME FARE UNA DIVISIONE
La divisione in colonna
Le divisioni si eseguono sempre partendo da sinistra.
Eseguiamo la seguente divisione 5244,38 : 6
La prima quantità di cifre che prendo in considerazione non può essere più piccola del divisore.
Successivamente si prendono le cifre una per una.
Successivamente si prendono le cifre una per una.
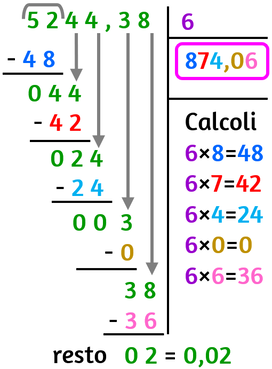
Prendiamo la prima cifra a sinistra:
- quante volte il 6 è contenuto nel 5? Neanche una volta.
- quante volte il 6 è contenuto nel 52? 8 volte.
- Scrivi 8 nella parte dedicata al risultato .
- Scrivi sotto il 52 il risultato di 6 x 8 = 48, fai la sottrazione e trova il rest
- Scrivi 7 nella parte dedicata al risultato di fianco all’ 8
- Scrivi sotto il 44 il risultato di 6 x 7 = 42, fai la sottrazione e trova il resto.
- quante volte il 6 è contenuto nel 24? 4 volte.
- Scrivi 4 nella parte dedicata al risultato di fianco all’ 87
- Scrivi sotto il 24 il risultato di 6 x 4 = 24, fai la sottrazione e trova il resto.
- quante volte il 6 è contenuto nel 3? 0 volte.
- Scrivi ,0 nella parte dedicata al risultato di fianco all’ 874
- Mettiamo anche la virgola perché la cifra che abbiamo abbassato in questo passaggio si trova immediatamente dopo la virgola.
- Scrivi sotto il 3 il risultato di 6 x 0 = 0, fai la sottrazione e trova il resto.
- quante volte il 6 è contenuto nel 38? 6 volte.
- Scrivi 6 nella parte dedicata al risultato di fianco all’ 874,0
- Scrivi sotto il 38 il risultato di 6 x 6 = 36, fai la sottrazione e trova il resto.
⚠ Se vuoi continuare la divisione puoi farlo aggiungendo degli zeri al dividendo.
Come si eseguono le divisioni se il divisore è un numero con la virgola?
Prima di trasformare la divisione seguiamo un pochino di regole:
- il divisore non deve avere la virgola
- il dividendo deve avere cifre decimali in quantità maggiore rispetto al divisore
- se il dividendo è un numero intero metti la virgola e poi aggiungi tanti zeri quante sono le cifre decimali nel divisore
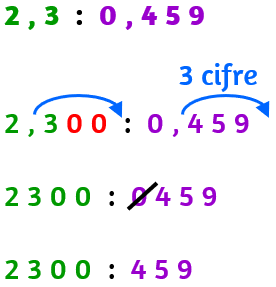
- se sia dividendo che divisore sono numeri decimali aggiungi tanti zeri «inutili» al dividendo in modo da avere la stessa quantità di cifre decimali presenti nel divisore.
Vediamo alcuni esempi:
|
|
Dividere un numero naturale o decimale per 10, 100, 1000
Quando divido un numero per 10 ciascuna cifra diminuisce il proprio valore di un ordine di grandezza: le centinaia diventano decine, le decine diventano unità, le unità diventano decimi, i decimi diventano centesimi, ...
Quando divido un numero per 100 ciascuna cifra diminuisce il proprio valore di due ordini di grandezza: le centinaia diventano unità, le decine diventano decimi, le unità diventano centesimi, i decimi diventano millessimi, ...
|
Supponiamo di voler svolgere la seguente divisione:
|
LE PROPRIETÀ DELLA DIVISIONE
Proprietà invariantiva
Invariare = che non cambia
Se moltiplico o divido per una stessa quantità
sia al dividendo che il divisore il quoziente non cambia.
sia al dividendo che il divisore il quoziente non cambia.
Grazie a questa proprietà è possibile trasformare una divisione in un'altra più semplice, dividendo tante volte, e talvolta moltiplicando, per una stessa quantità, entrambi i termini della divisione.
Vediamo alcuni esempi di come è possibile semplificare una divisione apparentemente complicata.
- Dividere un numero per 5
quando vuoi dividere un numero per 5, rendi più semplice la divisione moltiplicando per 2 sia il dividendo che il divisore:
284 : 5 = (284 × 2) : (5 × 2) = 568 : 10 = 56,8
in questo modo il divisore diventa 10 e la divisione è diventata molto più facile.
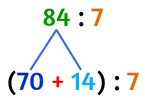
Proprietà distributiva rispetto all'addizione
Distribuire = dare agli altri
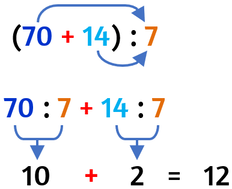
Il quoziente di una divisione, il cui dividendo può essere scritto come una somma, può essere calcolato facendo la somma tra il quoziente del primo addendo per il divisore e il quoziente del secondo addendo per lo stesso divisore.
Riscrivo il dividendo come un’addizione
Divido entrami i termini dell’addizione per il divisore
Proprietà distributiva rispetto alla sottrazione
Il quoziente di una divisione, il cui dividendo può essere scritto come una differenza, può essere calcolato facendo la differenza tra il quoziente del minuendo e il divisore e il sottraendo per lo stesso divisore.
Riscrivo il dividendo come una sottrazione
Divido sia il minuendo che il sottraendo per il divisore
Un pochino di operazioni e di espressioni
Clicca qui per avere delle operazioni e delle espressioni con i numeri naturali.
Il tutto è stato preso dal sito Progetto Matematika - www.matematika.it
Il tutto è stato preso dal sito Progetto Matematika - www.matematika.it
|
|
Pagina revisionata il 14 giugno 2021
|