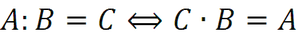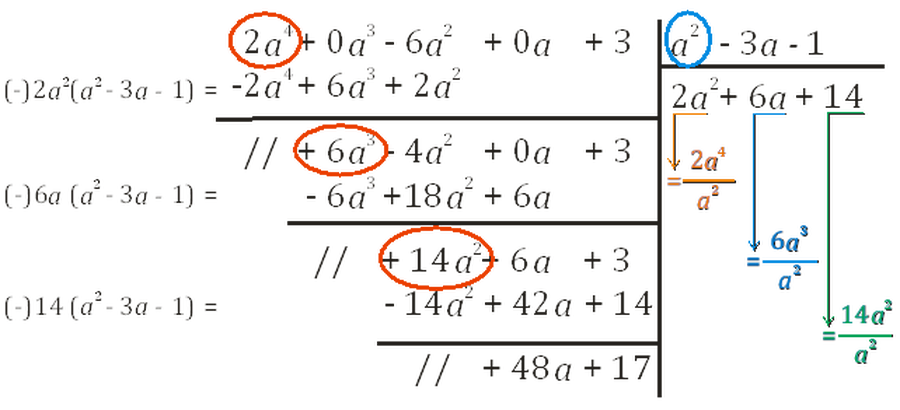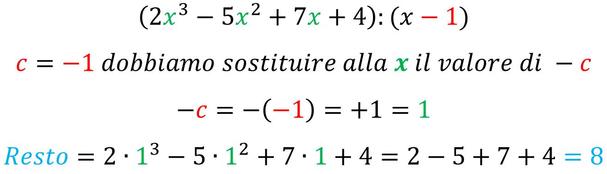Divisione di un polinomio per un polinomio
Un polinomio è divisibile per un altro polinomio quando non abbiamo resto.
Avviene come in aritmetica, un numero è divisore di un altro quando lo divide in parti uguali senza avere resto.
Definizione: si dice che un polinomio A è divisibile per un polinomio B quando esiste un polinomio C che moltiplicato per quello B dà come risultato il polinomio A.
Avviene come in aritmetica, un numero è divisore di un altro quando lo divide in parti uguali senza avere resto.
- 6 è divisore di 18 perché 18:6=3 resto 0
- 5 non è divisore di 21 perché 21:5=4 resto 1
Definizione: si dice che un polinomio A è divisibile per un polinomio B quando esiste un polinomio C che moltiplicato per quello B dà come risultato il polinomio A.
A = polinomio dividendo
B = polinomio divisore
C = polinomio quoto o quoziente
B = polinomio divisore
C = polinomio quoto o quoziente
Algoritmo per la determinazione del quoziente e del resto
Divisione di un polinomio per un polinomio
1) Scrivere il dividendo e il divisore in modo ordinato e completo
1) Scrivere il dividendo e il divisore in modo ordinato e completo
2) Costruire una tabella nella quale porre sulla sinistra il dividendo, sulla
destra il divisore e sotto il divisore quello che diverrà il quoziente
destra il divisore e sotto il divisore quello che diverrà il quoziente
3) Dividere il primo termine del dividendo con il primo termine del divisore
4) Scrivere il risultato ottenuto nella parte dedicata il quoziente
5) Moltiplicare ogni termine del divisore per il quoziente appena ottenuto e
cambiarlo di segno, avendo cura di scriverlo al di sotto di ogni monomio simile.
6) Sommare monomio a monomio, facendo attenzione che il primo deve dare
assolutamente valore zero
8) Dividere il primo termine del nuovo dividendo per il primo termine del divisore
9) Continua dal punto 4) fino a quando il primo termine del nuovo dividendo non
sarà minore del divisore, ciò che rimarrà sarà il resto della divisione
4) Scrivere il risultato ottenuto nella parte dedicata il quoziente
5) Moltiplicare ogni termine del divisore per il quoziente appena ottenuto e
cambiarlo di segno, avendo cura di scriverlo al di sotto di ogni monomio simile.
6) Sommare monomio a monomio, facendo attenzione che il primo deve dare
assolutamente valore zero
8) Dividere il primo termine del nuovo dividendo per il primo termine del divisore
9) Continua dal punto 4) fino a quando il primo termine del nuovo dividendo non
sarà minore del divisore, ciò che rimarrà sarà il resto della divisione
Ricapitolando:
Teorema del resto
Se abbiamo la divisione di un polinomio per un binomio del tipo x + c, allora è possibile conoscere il resto della divisione senza per questo doverla eseguire.
Per trovare il resto dovremo:
Per trovare il resto dovremo:
- sostituire alla variabile x il termine noto cambiato di segno (-c)
- risolvere l'espressione così ottenuta
Esempio
Esempio
|
|
contatore inserito il 15 luglio 2021
|