Gli insiemi

CARATTERISTICHE DEGLI INSIEMI

Cos'è un insieme matematico?

Si chiama insieme un raggruppamento, un contenitore virtuale, nel quale i suoi componenti sono stabiliti con certezza.
In un insieme matematico esiste un criterio oggettivo (che è uguale per tutti) che permette di indicare, in modo univoco, se un elemento fa parte di quell'insieme oppure no.

Un insieme può essere matematico o non matematico:

matematico

La caratteristica è oggettiva

gli oggetti nell’astuccio di Sara
le canzoni italiane
le lettere della parola «ginnastica»
i numeri pari minori di 15

non matematico

La caratteristica non è oggettiva

i cantanti più bravi
gli amici più simpatici
i piatti più buoni
i numeri «fortunati» al lotto

I componenti di un insieme si chiamano elementi.
Gli elementi di un insieme si indicano con le lettere minuscole dell'alfabeto (a, b, c, ...).
Gli elementi che compongono un insieme possono essere sia oggetti reali che oggetti astratti: numeri, lettere, figure, animali, persone, ....

I simboli ∈ e ∉

∈ → l’elemento appartiene (fa parte) dell’insieme che sto considerando
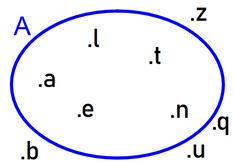
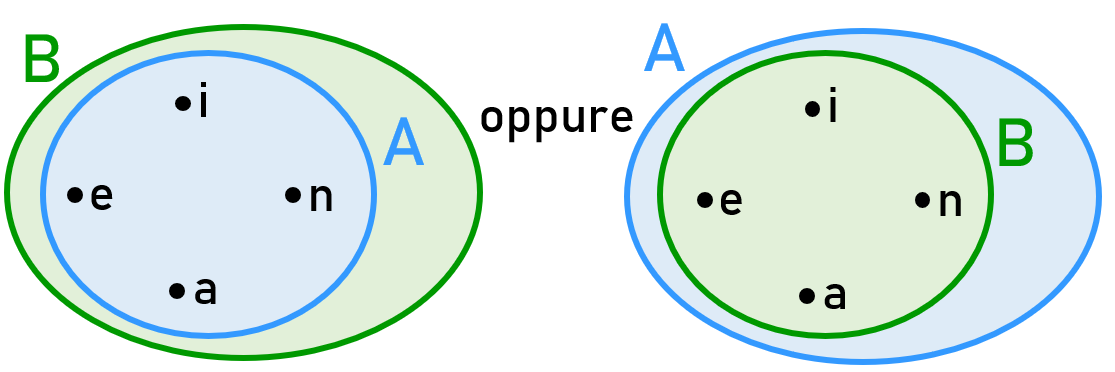
∉ → l’elemento NON appartiene (non fa parte) dell’insieme che sto considerando

Consideriamo l’insieme A costituito dalle lettere della parola «altalena», di sicuro possiamo affermare che:
a ∈ A → l’elemento a (la lettera a) appartiene all’insieme A
b ∉ A → l’elemento b (la lettera b) non appartiene all’insieme A
z ∉ A → l’elemento z (la lettera z) non appartiene all’insieme A
l ∈ A → l’elemento l (la lettera l) appartiene all’insieme A

L'insieme vuoto

Non ha elementi.
Per indicare questo insieme si usa il simbolo ∅.
L'insieme al suo interno, nella rappresentazione grafica, non ha nessun elemento.

Sono esempio di insiemi vuoti:

le consonanti nella parola aia
i numeri dispari divisibili per 2
i triangoli con 4 lati

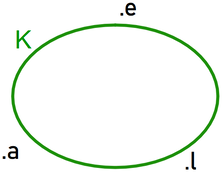
Consideriamo l'insieme K dei numeri che compongono la parola "leale"
K = {∅}
K = {x|x è un numero nella parola "leale"}

Gli insiemi finiti

Hanno un numero limitato di elementi.
Anche se sono molto numerosi li potrei contare.
Può avere anche solo un elemento.

Sono esempi di insiemi finiti:

gli alunni della classe 1^E
i numeri pari minori di 10
i granelli di sabbia nella spiaggia del Poetto

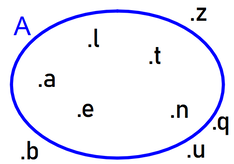
L'insieme A delle lettere della parola altalena.
A = {x|x è una lettera della parola altalena}
A = {a; l; t; e; n}

Gli insiemi infiniti

Ha un numero infinito di elementi.
Non esiste una fine in questo insieme.

Sono esempi di insiemi infiniti:

i numeri pari
i multipli di 5
i triangoli con un lato di 3 cm

L'insieme F dei numeri multipli di 3.
F = {x|x è un multiplo di 3}
F = {3; 6; 9; 12; 15; ...}

Un insieme infinito non può essere rappresentato graficamente.