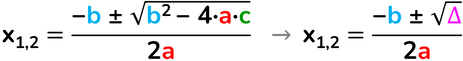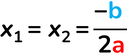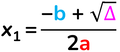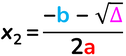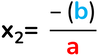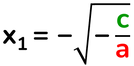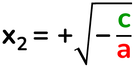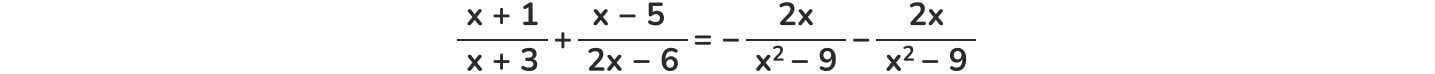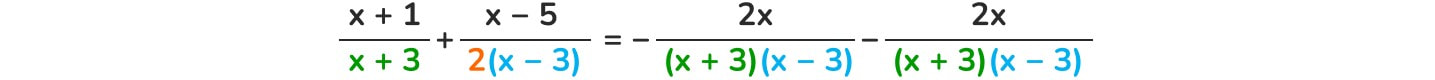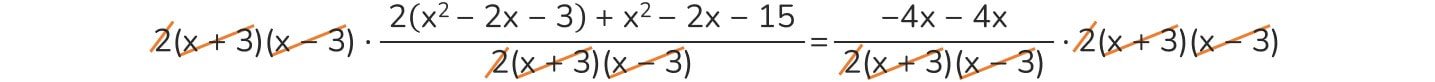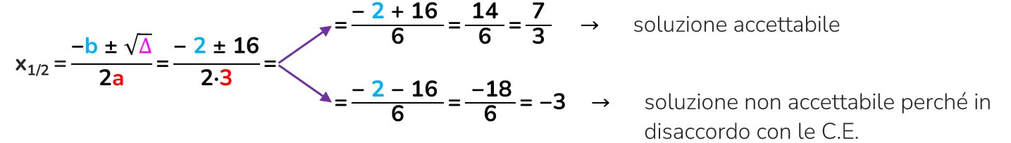Le equazioni di II grado
Un'equazione si dice di II grado quando l'incognita col grado maggiore è al quadrato (elevato 2).
Risolvere un'equazione di II grado vuol dire trovare quei valori che sostituiti all'incognita rendono vera l'uguaglianza, il valore del I membro sia uguale al valore del II membro.
Sono esempi di equazioni di secondo grado:
Risolvere un'equazione di II grado vuol dire trovare quei valori che sostituiti all'incognita rendono vera l'uguaglianza, il valore del I membro sia uguale al valore del II membro.
Sono esempi di equazioni di secondo grado:
|
5x² = 0
z² + z = 0 |
2x² – 9x + 1 = 0
x² – x – 6 = 0 |
3x² – 8 = 0
2x² + 11 = 0 |
In ciascuna delle sei equazioni, l'incognita col grado maggiore è sempre al quadrato. Questa è la condizione necessaria affinché possa definirsi un'equazione di II grado.
In linea generale, se noi abbiamo un'equazione, essa sarà di secondo grado quando potrà essere espressa in questa forma:
In linea generale, se noi abbiamo un'equazione, essa sarà di secondo grado quando potrà essere espressa in questa forma:
ax² + bx + c = 0
con a ≠ 0 sempre, in caso contrario l'equazione non sarebbe di secondo grado
con a ≠ 0 sempre, in caso contrario l'equazione non sarebbe di secondo grado
Classificazione delle equazioni di II grado
Un'equazione di II grado si dice:
- completa, quando sia il coefficiente della x che il termine noto sono diversi da zero;
- incompleta, quando o il coefficiente della x, o il termine noto o entrambi sono uguali a zero.
|
EQUAZIONI COMPLETE
ax² + bx + c = 0
b ≠ 0 e c ≠ 0
|
EQUAZIONI INCOMPLETE
|
RISOLUZIONE DI UN'EQUAZIONE DI II GRADO
(sia completa che incompleta)
Risolvere un'equazione vuol dire trovare quei valori da sostituire all'incognita.
D'ora in poi useremo per comodità la sola incognita x.
Quasi tutte le equazioni di II grado sono scomponibili, pertanto se noi riusciamo a scomporre la nostra equazione di II abbiamo conseguentemente trovato i valori che la rendono vera.
I matematici hanno trovato una formula, che seppur complessa ad un primo sguardo, costituisce uno strumento meraviglioso che ci permette di trovare i valori che stiamo ricercando senza per forza scomporre.
D'ora in poi useremo per comodità la sola incognita x.
Quasi tutte le equazioni di II grado sono scomponibili, pertanto se noi riusciamo a scomporre la nostra equazione di II abbiamo conseguentemente trovato i valori che la rendono vera.
I matematici hanno trovato una formula, che seppur complessa ad un primo sguardo, costituisce uno strumento meraviglioso che ci permette di trovare i valori che stiamo ricercando senza per forza scomporre.
Ma prima di utilizzare una qualsiasi formula sarà necessario scrivere in forma normale la nostra equazione:
- risolvere le operazioni in eventuali parentesi;
- portare tutto al I membro e uguagliarlo a zero;
- semplificare mettendo insieme tutti i termini simili.
Il valore delle due x che annullano la mia equazione sono:
Per prima cosa occorre calcolare il delta attraverso la formula:
Δ = b² – 4ac
Se il valore del delta non è minore di zero possiamo estrarre la sua radice quadrata. Dopo di che sostituiamo il tutto nella formula sopra.
Possiamo trovare tre diversi casi:
|
Δ < 0
|
Non ci sono soluzioni
Non si può scomporre Nessun numero reale può far diventare zero la nostra equazione La radice quadrata di un numero negativo è inammissibile nell'insieme dei numeri reali, infatti nessun numero reale (positivo o negativo) elevato al quadrato darà mai un numero negativo.
Il trinomo con delta minore di zero non ammette scomposizione e si riscrive così com'è.
3x² + 4x + 5
calcoliamo il suo delta Δ = b² – 4ac = 4² – 4 · 3 · 5 = 16 – 60 = –44 poiché il delta è negativo non si può scomporre: 3x² + 4x + 5 = 3x² + 4x + 5 Non esiste nessun valore che sostituito alla x renda zero il valore dell'equazione.
Da questo ne consegue che questo tipo di espressione è sempre maggiore di zero e non è mai né uguale a zero né minore di zero. |
|
Δ = 0
|
Due valori coincidenti
Si tratta del quadrato di un binomio La radice quadrata di zero è sempre uguale a zero, pertanto otteniamo un unico valore.
Il trinomio scomposto equivale così al quadrato di un binomio:
9x² – 12x + 4
calcoliamo il suo delta Δ = b² – 4ac = (–12)² – 4 · 9 · 4 = 144 – 144 = 0 x₁ = x₂ = – b : 2a = – (–12) : (2 · 9) = 12/18 = 2/3 Poiché nell'equazione non compaiono termini frazionari daremo alla x come coefficiente il denominatore della frazione e lasceremo come termine noto il numeratore della stessa frazione come risultato.
Ricorda: lo zero dell'equazione corrisponde al suo opposto nella scomposizione. (3x – 2)(3x – 2) = (3x – 2)²
|
|
Δ > 0
|
Due valori distinti
Si tratta di un trinomio particolare La radice quadrata di un numero positivo ammette sempre due valori, opposti tra di loro, perché un numero al quadrato, positivo o negativo, dà sempre un valore positivo.
x² – x – 12
calcoliamo il suo delta Δ = b² – 4ac = (–1)² – 4 · 1 · (–12) = 1 + 48 = 49 radice quadrata di 49 = 7 x₁ = (–b + 1) : 2a = [– (–1) + 7] : (2 · 1) = 8 : 2 = 4 x₂ = (–b – 1) : 2a = [– (–1) – 7] : (2 · 1) = – 6 : 2 = –3 x₁ = 4 e x₂ = –3 Il trinomio scomposto sarà uguale ad un binomio per un altro binomio, dove i termini noti di ciascun binomio sono uguali agli opposti degli zeri dell'equazione appena trovati:
(x – 4)(x + 3)
|
Ricapitolando, in pratica cosa devo fare?
- riscrivo in forma normale l'equazione;
- metto in evidenza i coefficienti a, b e c;
- scrivo la formula per il calcolo del delta;
- sostituisco nella formula del delta i valori di a, b e c;
- se il delta è maggiore o uguale a zero calcolo la sua radice quadrata;
- infine calcolerò i due valori della x.
Il valore di un'equazione incompleta senza il calcolo del Δ
Ora vediamo che tipo di soluzioni abbiamo nei diversi tipi di equazione incomplete (tenendo conto che la formula sopra può essere sempre utilizzata).
Equazioni incomplete spurie
Ammettono sempre due soluzioni reali distinte.
|
ax² + bx = 0
|
b ≠ 0 e c = 0
|
Ammette due soluzioni distinte, di cui una uguale a zero e l'altra diversa da zero, qualunque sia il valore di b.
Vediamo ora di scomporre l'equazione per trovare il valore da poter dare all'incognita per ottenere l'uguaglianza a zero
ax² + bx = 0
x₁(ax₂ + b) = 0
x₁(ax₂ + b) = 0
Equazioni incomplete pure
Se a e c sono concordi non esiste soluzione nell'insieme dei numeri reali.
Se a e c sono discordi allora esistono due soluzioni reali opposte.
Se a e c sono discordi allora esistono due soluzioni reali opposte.
|
ax² + c = 0
|
b = 0 e c ≠ 0
|
Ammette due soluzioni opposte, solo se c è negativo, cioè minore di zero.
se c < 0
Equazioni incomplete monomie
|
ax² = 0
|
b = 0 e c = 0
|
Il valore della x è sempre uguale a zero.
x₁ = x₂ = 0