LO SPAZIO TRIDIMENSIONALE
Sino ad ora abbiamo lavorato con al massimo due dimensioni.
Oggetti geometrici che non hanno dimensioni: il punto.
Oggetti geometrici che hanno una dimensione: le linee e i segmenti.
Oggetti geometrici che hanno due dimensioni: le figure che possono essere disegnate in un piano, gli angoli.
D’ora in poi lavoreremo con gli oggetti geometrici che più si avvicinano alla realtà: le figure solide o tridimensionali. I corpi che troviamo in natura hanno forme geometriche irregolari, pertanto l’uomo ha cercato di «semplificare» le cose creando dei solidi che avessero caratteristiche simili a quelle naturali ma forme più semplici da riprodurre.
Oggetti geometrici che non hanno dimensioni: il punto.
Oggetti geometrici che hanno una dimensione: le linee e i segmenti.
Oggetti geometrici che hanno due dimensioni: le figure che possono essere disegnate in un piano, gli angoli.
D’ora in poi lavoreremo con gli oggetti geometrici che più si avvicinano alla realtà: le figure solide o tridimensionali. I corpi che troviamo in natura hanno forme geometriche irregolari, pertanto l’uomo ha cercato di «semplificare» le cose creando dei solidi che avessero caratteristiche simili a quelle naturali ma forme più semplici da riprodurre.
LE RETTE NELLO SPAZIO TRIDIMENSIONALE
Sino ad ora abbiamo visto rette e segmenti nel piano.
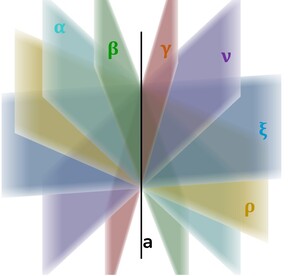
Sono infiniti i piani che possono contenere una singola retta (figura a fianco): per la retta a passano i piani α, β, γ, ν, ξ, ρ, ...
Per una retta e un punto non appartenente alla retta passa uno e un solo piano.
Per tre punti distinti non allineati passa uno e un solo piano.
Sono infiniti i piani che possono contenere una singola retta (figura a fianco): per la retta a passano i piani α, β, γ, ν, ξ, ρ, ...
Per una retta e un punto non appartenente alla retta passa uno e un solo piano.
Per tre punti distinti non allineati passa uno e un solo piano.
Complanari → si dice di due o più oggetti che appartengono allo stesso piano.
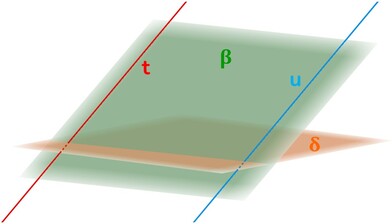
Due rette parallele sono sempre complanari e hanno costante la loro distanza: le rette t e u sono parallele e appartengono contemporaneamente allo stesso piano β.
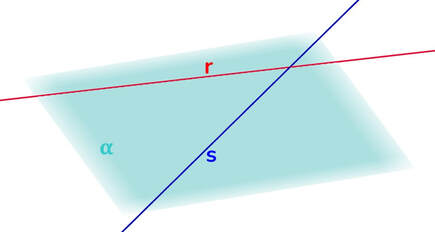
Due rette incidenti sono sempre complanari (esiste sempre un piano capace di contenerle entrambe): le rette r e s sono incidenti e appartengono contemporaneamente al piano α.
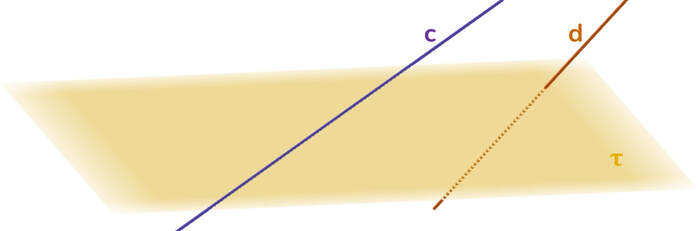
Due rette non complanari e non incidenti si dicono sghembe. In questo caso particolare non esiste un piano capace di contenerle entrambe contemporaneamente: tra i piani passanti per la retta c non esiste nessun piano in comune capace di contenere anche la retta d.
I DIVERSI TIPI DI SOLIDO
- Solido → qualunque figura che occupa uno spazio tridimensionale, dotato quindi di un estensione in tre dimensioni diverse e tra loro perpendicolari.
- Superficie → quella parte del solido che lo delimita dallo spazio esterno.
- Poliedro → solido la cui superficie esterna è delimitata da poligoni.
- Solido a superficie curva → un solido la cui superficie esterna è delimitata da almeno una superficie curva (che non può essere riprodotta in un piano).
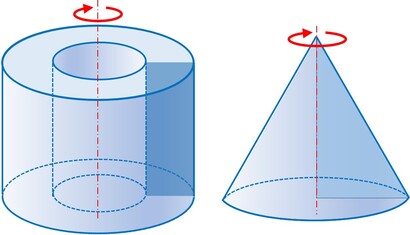
- Solido di rotazione → solido generato dalla rotazione di una figura piana attorno ad un asse interno o esterno alla superficie delle figura che ruota. I solidi di rotazione sono anche solidi a superficie curva.
- Solido irregolare → qualunque solido non riconducibile ai solidi visti sopra.
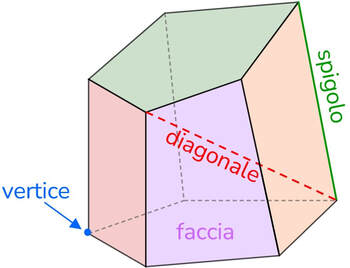
Poliedri
In un poliedro possiamo distinguere:
- Faccia → ciascuno dei poligoni che formano la superficie del poliedro.
- Spigolo → sono i lati dei poligoni che costituiscono le facce del poliedro.
- Vertice → ciascuno dei punti nei quali convergono le facce, sono così gli estremi di ciascuno spigolo.
- Diagonale → segmento che ha come estremi due vertici non appartenenti alla stessa faccia.
Tutta la sua superficie di un poliedro è tassellata di poligoni.
Solidi a superficie curva
Tutta la loro superficie ha superfici curve (non riproducibili in un foglio) e talvolta anche da superfici piane.
Solidi di rotazione
Sono solidi che si ottengono facendo ruotare figure piane (poligoni o a contorno curvilineo o misto) attorno ad un asse di rotazione.
Solidi irregolari
Sono solidi che non appartengono alle categorie già viste. Si tratta generalmente di oggetti non antropici e quindi creati dalla natura.
IL VOLUME E LA CAPACITÀ
Volume → spazio tridimensionale occupato da un solido.
Misura l’estensione tridimensionale dell’oggetto nello spazio.
Nell’oggetto rappresentato sotto, un bicchiere, il volume è rappresentato dallo spazio occupato dal bicchiere sottratto lo spazio vuoto che può essere occupato da un liquido.
Misura l’estensione tridimensionale dell’oggetto nello spazio.
Nell’oggetto rappresentato sotto, un bicchiere, il volume è rappresentato dallo spazio occupato dal bicchiere sottratto lo spazio vuoto che può essere occupato da un liquido.
Capacità → il volume esterno che può essere contenuto da un oggetto, detto contenitore, che presenta così una cavità.
Nell’oggetto rappresentato a fianco, la capacità del bicchiere è rappresentata dalla quantità massima di liquido che il bicchiere può contenere.
Nell’oggetto rappresentato a fianco, la capacità del bicchiere è rappresentata dalla quantità massima di liquido che il bicchiere può contenere.
Solidi equivalenti → si dice di due solidi che occupano lo stesso volume.
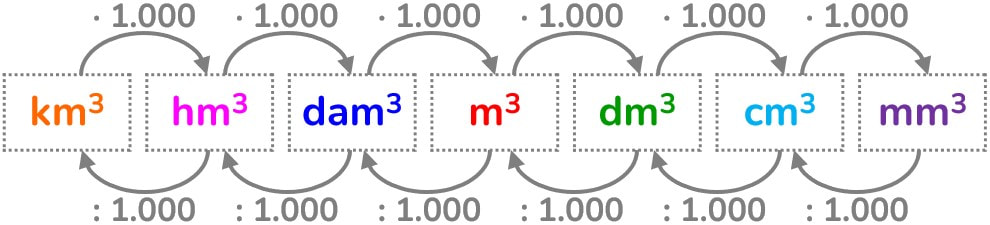
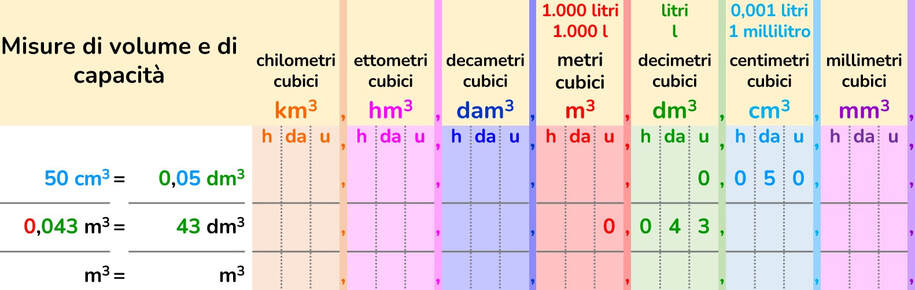
Il volume generalmente si esprime in multipli e sottomultipli del metro cubico o metro cubo (m³), il volume di liquido contenuto in un altro oggetto o il volume che può ospitare un contenitore si può esprimere sia in multipli e sottomultipli del metro cubo che del litro.
Misurare il volume di un solido o la capacità di un recipiente può essere cosa semplice se questi hanno forme semplici riconducibili a formule ben precise.
Se un oggetto ha una forma irregolare e magari è poroso può essere difficile misurarne il volume, ma, in questo caso possono essere usati degli stratagemmi:
- si immerge il solido in un liquido che non ne aumenta l’estensione della superficie esterna ma che riempie eventuali fessure, rendendolo così impermeabile;
- ora si immerge il solido in un cilindro graduato nel quale è presente un liquido in quantità nota (ad esempio 200 ml);
- misuriamo il livello raggiungo dal liquido dopo l’immersione del solido (ad esempio 280 ml);
- facciamo la differenza tra il livello dopo l’immersione e quello invece prima dell’immersione, in questo caso faremo 280 ml – 200 ml = 80 ml, questo che abbiamo trovato è il volume dell’oggetto che è stato immerso.