Le operazioni con gli angoli
Scrivere in forma normale una misura angolare
Scrivere in forma normale una misura angolare vuol dire avere:
- i secondi minori di 60
- i primi minori di 60
- si parte dai secondi
- se i secondi sono maggiori di 60 si farà → secondi : 60 secondi = x primi resto = y secondi
- la quantità x ottenuta sono i primi, il resto y sono i secondi rimasti
- aggiungi i primi ottenuti dalla divisione ai primi che avevi già
- se anche i primi totali sono maggiori di 60 si farà → primi : 60 primi = a gradi resto = b primi
- la quantità a ottenuta sono i gradi, il resto b sono i primi rimasti
- aggiungi i gradi ottenuti dalla divisione ai gradi che avevi già
gradi primi secondi → gradi+a° b' y″
|
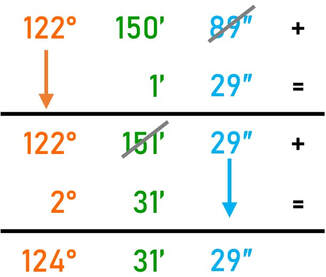
Esercizio: scrivi in forma normale la misura angolare 122° 150' 89″
|
|
Ora né i primi né i secondi sono maggiori di 60, hai ridotto in forma normale la misura angolare.
L'operazione di addizione
Sommare tra loro gli angoli non è un'operazione diversa da quella fatta con i numeri, ma come hai già imparato quando fai l'addizione in colonna puoi sommare solo oggetti che hanno le stesse caratteristiche, per cui:
- metti i secondi nella colonna dei secondi e esegui la somma;
- metti i primi nella colonna dei primi e esegui la somma;
- metti i gradi nella colonna dei gradi e esegui la somma;
- scrivi in forma normale la misura ottenuta.
|
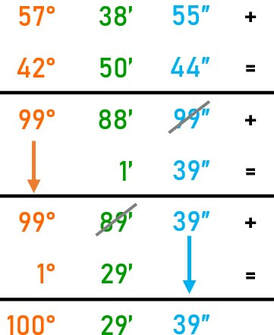
Esercizio: esegui l'addizione 57° 38' 55″ + 42° 50' 44″ e esprimi la somma in forma normale
|
|
L'operazione di moltiplicazione
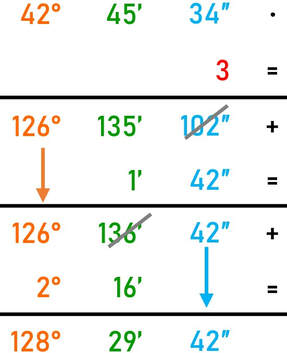
Moltiplicare la misura angolare per una determinata quantità non è un'operazione diversa da quella fatta con i numeri. Ricorda di moltiplicare per la quantità determinata:
- i secondi;
- i primi;
- i gradi;
|
Esercizio: esegui la moltiplicazione 42° 45' 34″ · 3 e esprimi il prodotto in forma normale
|
|
Ora il risultato della moltiplicazione è scritto in forma normale.
L'operazione di sottrazione
Si potrebbe pensare che la sottrazione, come le altre operazioni che abbiamo visto, sia praticamente uguale.
Questo è vero se le quantità da togliere sono minori del minuendo, sennò occorre fare un prestito.
Ed è proprio il prestito l'insidia di questa operazione.
Se la quantità da togliere è maggiore del minuendo occorre un prestito dal compagno a sinistra:
Questo è vero se le quantità da togliere sono minori del minuendo, sennò occorre fare un prestito.
Ed è proprio il prestito l'insidia di questa operazione.
Se la quantità da togliere è maggiore del minuendo occorre un prestito dal compagno a sinistra:
- se occorrono secondi, si chiederà il prestito ai primi;
- se occorrono i primi, si chiederà il prestito ai gradi.
- se i gradi fanno un prestito ai primi, ai primi occorrerà aggiungere 60, perché 1°=60', mentre i gradi diminuiranno di 1;
- se i primi fanno un prestito ai secondi, ai secondi sarà aggiunto 60, perché 1'=60'', mentre i primi diminuiranno di 1.
|
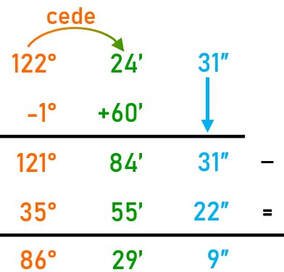
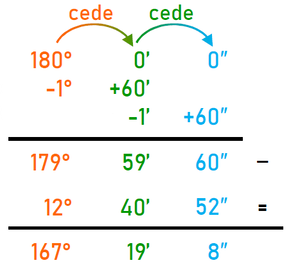
Esercizio: esegui la sottrazione 122° 24' 31″ - 35° 55' 22″
|
|
|
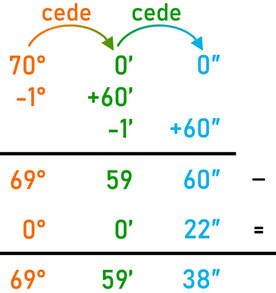
Esercizio: esegui la sottrazione 70° - 22″
|
|
Esercizio: esegui la sottrazione 122° 24' 31″ - 35° 55' 22″
|
|
L'operazione di divisione
Innanzitutto un pochino di regole:
- Prima si dividono i gradi, poi i primi e infine i secondi
- Le divisioni si eseguono sempre la prima cifra o il primo gruppo di cifre a sinistra.
- Se la divisione è esatta, si passa alla parte successiva.
- Se la divisione non è esatta, e ha un resto, ricorda di trasformare il resto:
1° = 60', 2° = 120', 3° = 180' … oppure 1' = 60'', 2' = 120'', 3' = 180''...
che dovrà essere aggiunto alla misura alla sua destra
|
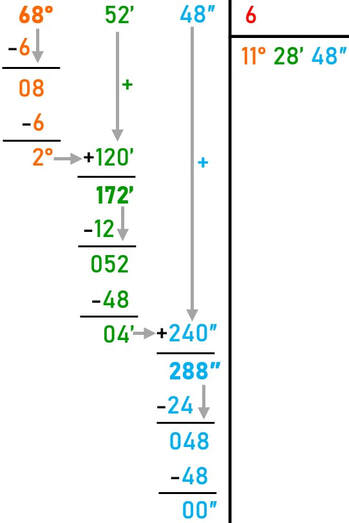
Esercizio: esegui la divisione 68° 52' 48″ : 6
|
|
Rette parallele intersecate da una trasversale
Nell'immagine sotto, se vuoi spostare le rette devi agire sui punti che compaiono dopo aver messo la spunta su "disegnamo 3 punti A, B e C".
|
|
Contatore inserito il 23 aprile 2021
|