CLASSIFICAZIONE DEI TRIANGOLI
​IN BASE AI LATI E IN BASE AGLI ANGOLI

CLASSIFICAZIONE DEI TRIANGOLI IN BASE AI LATI

I triangoli possono avere: 
- tutti e tre i lati tra loro congruenti;
- due dei suoi lati congruenti;
- i tre lati con misure tra loro diverse.

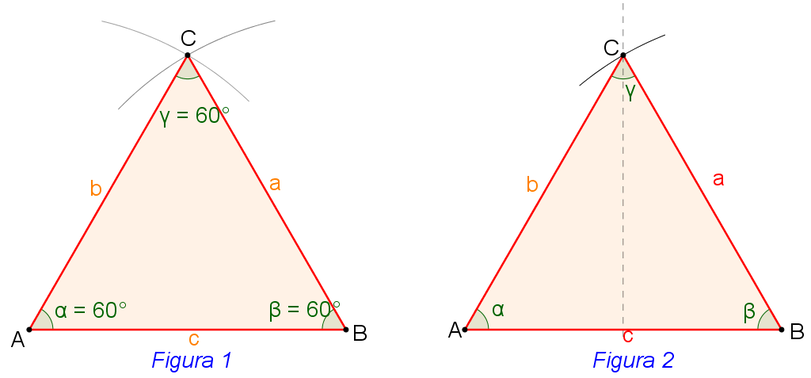
Triangoli equilateri

• Hanno tutti e tre i lati tra loro congruenti (hanno, cioè, la stessa misura)
• hanno tutti e tre gli angoli tra loro congruenti (misurano tutti 60°).
• l'altezza relativa a qualunque lato è nello stesso tempo bisettrice, mediana e asse

Due modi diversi per disegnare un triangolo equilatero

Materiale occorrente: righello, compasso e ​matita

Modo 1

1. disegnare il lato AB della misura che preferite;
2. aprire il compasso mettendo la punta in A e la mina in B;
3. disegnare 2 archi di circonferenza mettendo:
   - l'ago su A;
   - l'ago su B, fino ad incontrare l'arco precedente;
4. mettere in evidenza il punto di intersezione (punto in cui si incontrano i due archi) e denominarlo C;
5. unire il punto A con il punto C usando il righello;
6. unire il punto B con il punto C usando il righello;
7. avete disegnato il triangolo equilatero.

​Modo 2

1. disegnare il lato AB;
2. disegnare il segmento perpendicolare ad AB passante per il  punto medio di AB (abbiamo disegnato l'asse del segmento AB);
3. aprire il compasso mettendo la punta in A e la mina in B;
4. disegnare un arco di circonferenza puntando su A o su B e intersecare il segmento perpendicolare (cioè l'asse);
5. mettere in evidenza il punto di intersezione tra il segmento e l'arco, abbiamo ottenuto il vertice C del triangolo equilatero;
6. continuare dal punto 5 del modo 1.

---

Triangoli isosceli

Si chiama triangolo isoscele quel triangolo
​che ha due dei suoi lati tra loro congruenti.

Vediamo le sue caratteristiche, derivanti proprio dall'avere due lati della stessa lunghezza: 

• il lato diverso prende il nome di ​base
• i lati con la stessa misura (congruenti) prendono il nome di lati obliqui
• l'altezza relativa alla base è bisettrice dell'angolo opposto, è asse della stessa base, tagliando così in due triangoli rettangoli speculari
• gli angoli adiacenti alla base hanno la stessa ampiezza (sono congruenti) e sono sempre acuti

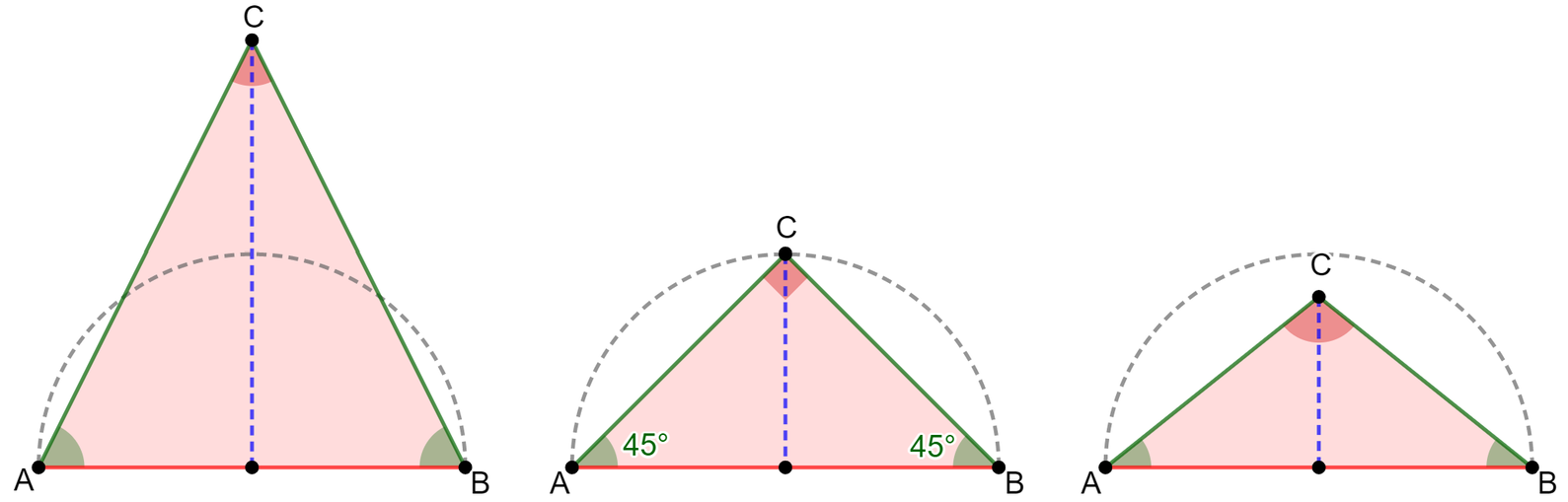
Triangolo isoscele
acutangolo​
il vertice C sta al di sopra della semicirconferenza

Triangolo isoscele 
rettangolo
il vertice C sta sulla semicirconferenza

Triangolo isoscele
ottusangolo
il vertice C sta al di sotto della semicirconferenza

Usa gli sliders per modificare le due immagini, che hanno in comune solo la misura della base. Per avere misure perfette fai un click sul pallino dello slider desiderato poi usa le frecce direzionali nella tua tastiera, verso l'alto (o verso destra) per aumentarne il valore o verso il basso (o verso sinistra) per diminuirlo.

---

Triangoli scaleni

I triangoli scaleni hanno:

• la misura di ogni lato è diversa da quella degli altri due;
• la misura di ogni angolo è diversa da quella degli altri due.

Ricordiamo che:
- ad angolo maggiore sta opposto lato maggiore e viceversa;
- ad angolo minore sta opposto lato minore.

CLASSIFICAZIONE DEI TRIANGOLI IN BASE AGLI ANGOLI

I triangoli possono avere: 

tutti e tre gli angoli acuti (tutti gli angoli più piccoli di 90°).

Il vertice blu del triangolo deve stare al di sopra della semicirconferenza e all'interno dello spazio tra le due rette parallele.

solo un angolo retto (90°) e gli altri due sono acuti (più piccoli di 90°).

​
​
Il vertice blu deve stare esattamente sulla semicirconferenza.

solo un angolo ottuso (più grande di 90°) e gli altri due acuti.
​
Il vertice blu deve stare all'interno del semicerchio (sotto la semicirconferenza ma sopra del lato più in basso).

Muovi il vertice blu per modificare la misura di due lati del triangolo. ​

Triangoli acutangoli

​Un triangolo è acutangolo quando tutti i suoi angoli interni sono ottusi (misurano meno di 90°).
Il triangolo equilatero è un tipo particolare di triangolo acutangolo.

Triangoli rettangoli

Un triangolo è rettangolo quando ha un angolo retto (misura esattamente 90°).
Nessun triangolo può avere più di un angolo retto.
Il triangolo rettangolo può essere o scaleno o isoscele.

Triangoli ottusangoli

Un triangolo è ottusangolo quando ha un angolo ottuso (misura più di 90°).
Nessun triangolo può avere più di un angolo ottuso.
Il triangolo ottusangolo può essere o scaleno o isoscele.

Nei triangoli vigono le regole:

• ad angolo maggiore sta opposto lato maggiore o a lato maggiore sta opposto angolo maggiore;
• ad angolo minore sta opposto lato minore o a lato minore sta opposto angolo minore;​

• la somma di due suoi lati è sempre maggiore del lato non considerato
  a + b > c                     a + c > b                    b + c > a
• la differenza di due suoi lati è sempre minore del lato non considerato
  |a – b| < c                  |a – c| < b                  |b – c| < a.

ATTENZIONE: le sottrazioni dentro le asticelle verticali | ... | devono essere svolte
​togliendo al più grande dei due il più piccolo dei due e non necessariamente nell'ordine in cui compaiono.​

Nello stesso triangolo non ci possono essere contemporaneamente:

• due angoli retti;
• due angoli ottusi;
• un angolo retto e un angolo ottuso.

contatore inserito il 23 agosto 2021