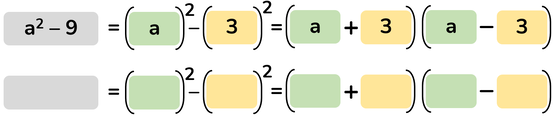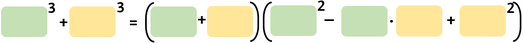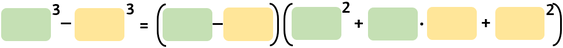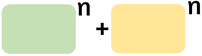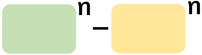|
|
SCOMPOSIZIONE DI UN POLINOMIO
Scomporre un polinomio vuol dire riscrivere il polinomio come prodotto di monomi e polinomi più piccoli a loro volta non scomponibili.
In pratica vuol dire cercare di capire quali prodotti tra polinomi o tra monomi hanno generato il polinomio che si intende scomporre.
In pratica vuol dire cercare di capire quali prodotti tra polinomi o tra monomi hanno generato il polinomio che si intende scomporre.
x⁵ – x⁴ – 7x³ + x² + 6x = x (x –3)(x – 1)(x + 1)(x + 2)
polinomio scomposizione
polinomio scomposizione
Non sono scomponibili:
- la somma di due quadrati;
- xⁿ + yⁿ → se n è pari (tranne nel caso in cui l'esponente sia in entrambi multiplo di 3 o di 4)
- quei polinomi di secondo grado il cui delta è minore di zero.
Raccoglimento totale a fattor comune o la messa in evidenza
Scomporre a fattore comune vuol dire calcolare il MCD tra i monomi di un polinomio e moltiplicare così il MCD per tutto ciò che non è in comune nel polinomio.
Supponiamo di voler scomporre il seguente polinomio: 15 x²y – 20 axy + 35 x⁴y²
- scompongo tutti i coefficienti (i numeri).
= 3 · 5 · x²y – 2² · 5 · a x y + 5 · 7 x⁴ y² =
- Che cos’hanno tutti quanti in comune? Hai trovato il MCD tra i monomi del polinomio.
5 xy = MCD
- Moltiplica il MCD per il polinomio e dividi ciascun monomio del polinomio per il loro MCD lasciando il polinomio dentro una parentesi.
= 5xy (15 x²y : 5xy – 20axy : 5xy + 35x⁴y² : 5xy) =
- Scrivi il MCD;
apri una parentesi;
scrivi i risultati delle singoli divisioni (tutto ciò che non è presente nel MCD);
chiudo la parentesi.
= 5xy (3x – 4a + 7x³y) hai trovato il tuo polinomio scomposto
Ricorda: se il MCD coincide con un monomio, dentro la parentesi dovrò mettere 1 al posto del monomio coincidente con il MCD.
12a⁴b² – 8a²b + 2a² =
calcoliamo ciò che hanno tutti i monomi in comune
12 = 2² · 3 8 = 2³ 2=2 → 2a² = MCD
scrivi il MCD → apri una parentesi → riscrivi il polinomio e dividi ciascun termine per il MCD
2a² [(12 a⁴b² : 2a²) – (8a²b : 2a²) + (2a² : 2a²)] =
= 2a² (6a²b² – 4b + 1)
calcoliamo ciò che hanno tutti i monomi in comune
12 = 2² · 3 8 = 2³ 2=2 → 2a² = MCD
scrivi il MCD → apri una parentesi → riscrivi il polinomio e dividi ciascun termine per il MCD
2a² [(12 a⁴b² : 2a²) – (8a²b : 2a²) + (2a² : 2a²)] =
= 2a² (6a²b² – 4b + 1)
Raccoglimento parziale
Quando ci troviamo di fronte ad un polinomio (composto da un numero non primo di monomi), talvolta non è possibile fare un raccoglimento totale ma possiamo notare che è possibile fare un raccoglimento parziale, cioè vedere se dei termini, a gruppi di 2 o di 3 o anche più, hanno in comune dei fattori.
|
Il raccoglimento totale è il primo metodo da usare quando dobbiamo scomporre un polinomio. |
Vogliamo scomporre la seguente somma algebrica: 3a²b – 2a + 12ab – 8 =
- esiste un fattore (numero o lettera) comune a tutti i monomi? NO
- Essendo un quadrinomio possono essere fatti solo gruppi di 2 monomi, la domanda è: ci sono due monomi che hanno in comune uno o più fattori?
Sì, il primo e il terzo monomio:
3a²b e 12ab
- Fai un raccoglimento tra il primo e il terzo monomio
3a²b + 12ab = 3ab (a + 4)
|
- Sostituisci alle due coppie di monomi la loro scomposizione
3a²b + 12ab – 2a – 8 =
= 3ab (a + 4) – 2 (a + 4)
- Che cos’hanno in comune le due scomposizioni?
l’elemento tra parentesi → (a + 4)
- Riscrivi l’elemento comune alle due scomposizioni e moltiplicalo per gli elementi non comuni alle due scomposizioni (ma comuni a ciascuna coppia presa inizialmente)
(a + 4)(3ab – 2)
Ora hai scomposto il quadrinomio usando la scomposizione parziale
Vogliamo scomporre la seguente somma algebrica:
2ab – 8a + 2b – 8 + 2bc – 8c
- Esiste un fattore (numero o lettera) comune a tutti i monomi? Sì
2ab – 8a + 2b – 8 + 2bc – 8c
- Fai un raccoglimento totale
2 (ab – 4a + b – 4 + bc – 4c)
- Essendo un polinomio composto da 6 monomi possiamo considerare gruppi di 2 o di 3 monomi.
- Sottolinea i monomi che intendi prendere in considerazione
2 (ab – 4a + b – 4 + bc – 4c) =
= 2 (ab + b + bc – 4a – 4 – 4c) =
- Applica un raccoglimento tra i termini considerati
ab + b + bc = b (a + 1 + c)
– 4a – 4 – 4c = – 4a (a + 1 + c)
- Scrivi il termine in comune a tutti
- Scrivi l’elemento comune ai due raccoglimenti parziali
- Dentro una parentesi scrivi gli elementi non comuni ai raccoglimenti parziali
2 (a + 1 + c)(b – 4a)
Vi propongo nel video alcuni esempi, che spero possano essere di vostro aiuto.
|
|
|
Scomposizione di un trinomio caratteristico o particolare
Il trinomio particolare è un trinomio nel quale, messo in ordine:
- il primo termine è un quadrato con coefficiente 1;
- mentre il secondo termine è data dalla loro somma o la loro differenza degli stessi due termini;
- il termine noto può essere visto come il prodotto di due numeri.
Nel trinomio vengono individuati due termini:
- somma (perché si tratta di una somma algebrica) → valore del coefficiente del secondo termine
- prodotto → valore del termine noto
Per svolgere questa scomposizione è necessario che si individuino due numeri relativi tali che: la loro somma dia il coefficiente del secondo termine, mentre il loro prodotto dia il valore del termine noto.
Il risultato della scomposizione è uguale al prodotto di due binomi, così composti:
- l'incognita e il primo numero;
- l'incognita e il secondo numero.
x² + (a + b)x + (a · b) =
= (x + a)(x + b)
= (x + a)(x + b)
Prodotto |
Somma |
Caratteristiche dei due numeri |
Esempi |
Positivo |
Positiva |
Concordi positivi |
x² + 5x + 4 = = x² + (4 + 1)x + (4 · 1)= = (x + 4)(x + 1) |
Positivo |
Negativa |
Concordi negativi |
x² – 5x + 4 = = x² – (4 + 1)x + (4 · 1) = = (x – 4)(x – 1) |
Negativo |
Positiva |
Discordi, il maggiore è positivo |
x² + 2x – 15 = = x² + (5 – 3)x – (5 · 3) = = (x + 5)(x – 3) |
Negativo |
Negativa |
Discordi, il maggiore è negativo |
x² – 2x – 15 = = x² – (5 – 3)x – (5 · 3) = = (x – 5)(x + 3) |
Lo svolgimento della scomposizione può essere svolta in due modi differenti:
- uno è quello indicato negli esempi;
- l'altro è quello di distribuire l'incognita ai termini individuati nella somma e fare poi un raccogliemento parziale.
Trinomio riconducibile ad un trinomio particolare
(o caratteristico)
Alcuni trinomi non possono essere definititi caratteristici perché il coefficiente del termine al quadrato è diverso da 1, ma sarà comunque possibile scomporlo attraverso altre strategie.
Con il trinomio caratteristico ha in comune:
Con il trinomio caratteristico ha in comune:
- il valore del prodotto = «coefficiente del termine al quadrato» · «il termine noto»;
- il valore della somma (o della differenza) dei valori = coefficiente del secondo termine.
Vogliamo scomporre il seguente trinomio: |
6x² – x – 2 |
Il termine noto è positivo o negativo? Cosa vuol dire? |
Il termine noto è –2 e vuol dire che i due numeri sono discordi |
Quali sono il valore del prodotto e della somma nel trinomio? |
Prodotto = 6 · –2 = –12 Somma = – 1 |
Quali numeri moltiplicati tra loro danno come valore il prodotto? |
12 · 1 = 6 · 2 = 4 · 3 |
Tra le coppie quali la loro differenza (prodotto negativo indica una differenza tra i valori assoluti) dà come valore quello della somma? |
12 - 1 = 11 6 - 2 = 4 4 – 3 = 1 |
Sostituisci alla somma nel trinomio i due valori numerici che hai trovato e distribuisci la x: |
6x² – (4 – 3) x – 2 = = 6x² – 4x + 3x – 2 = |
Fai un raccoglimento parziale tra i termini |
= 2x · (3x – 2) + 1 · (3x – 2)= = (3x – 2)(2x + 1) |
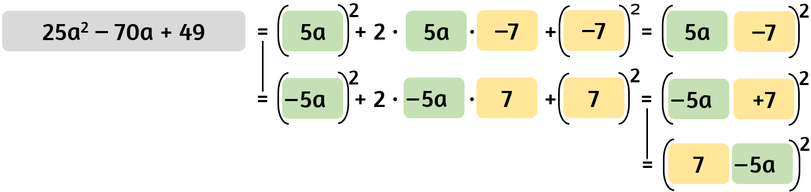
Riconoscere lo sviluppo del quadrato di un binomio
Lo sviluppo del quadrato di un binomio è:
- un TRINOMIO (polinomio formato da tre monomi);
- due dei suoi termini sono il quadrato di qualcosa e sono entrambi positivi o entrambi negativi;
- il termine che non è un quadrato ha quasi sempre coefficiente pari, se i coefficienti degli altri due termini sono numeri naturali, e può essere sia positivo che negativo.
|
Se i due quadrati sono negativi:
– b² + 2bc – c² =
= – (b² – 2bc + c²) |
|
|
Se il doppio prodotto è positivo: i termini del binomio sono concordi, o entrambi positivi o entrambi negativi.
|
Se il doppio prodotto è negativo: i termini del binomio sono discordi, se il primo termine è positivo il secondo sarà negativo e viceversa.
|
La differenza di due quadrati
è il prodotto di una somma per una differenza
|
La differenza di due quadrati la riconosci perché hai:
Importante: il numero 1 è uguale al quadrato di 1.
|
|
La scomposizione della differenza di due quadrati è uguale a:
- il prodotto di un binomio concorde per lo stesso binomio ma discorde;
- ciascun monomio nel binomio è uguale rispettivamente alla radice quadrata dei due monomi nella differenza, presi in valore assoluto.
Nella differenza dei due quadrati:
- il termine positivo sarà presente nei due binomi sempre con lo stesso segno (o positivo o negativo);
- il termine negativo sarà presente nei due binomi con segno opposto.
Scomposizione della somma di due cubi
Se hai di fronte un binomio concorde positivo e entrambi i termini sono dei cubi, la loro scomposizione sarà:
Se hai un binomio concorde negativo e entrambi i termini sono dei cubi, metti in evidenza il segno meno e scomponi come sopra.
Scomposizione della differenza di due cubi
Se hai di fronte un binomio discorde e entrambi i termini sono dei cubi, la loro scomposizione sarà:
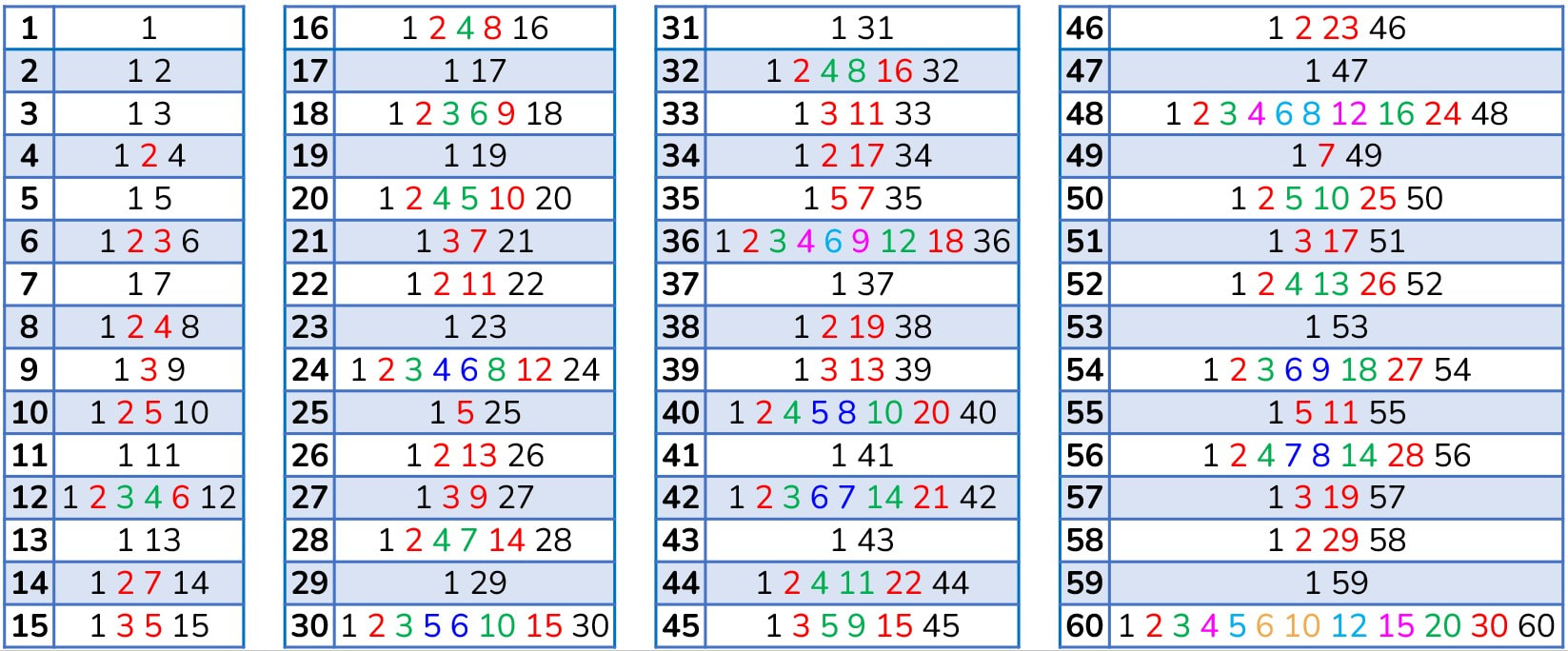
Scomposizione di binomi particolari
Se n è pari
Non si può scomporre per avere radici razionali. Se n è multiplo di 4 esiste una formula per poterlo scomporre che deriva dal completamento di un quadrato (scomposizione di Sophie Germain). Se n è dispari
È divisibile per la somma delle basi |
Se n è pari
È divisibile sia per la somma sia per la differenza delle basi Se n è dispari
È divisibile solo per la differenza delle basi |
Risoluzione di un caso particolare
(verrà poi approfondito negli studi universitari o in alcune classi dei licei scientifici -
si chiama il completamento del quadrato o scomposizione di Sophie Germain):
(verrà poi approfondito negli studi universitari o in alcune classi dei licei scientifici -
si chiama il completamento del quadrato o scomposizione di Sophie Germain):
|
x⁴ + 4 =
= x⁴ + 4 + 4x² – 4x² = = (x⁴ + 4 + 4x²) – 4x² = = (x² + 2)² – (2x)² = = (x² + 2 + 2x)(x² + 2 – 2x) |
Sembra il quadrato di un binomio ma manca il doppio prodotto, così aggiungiamo il doppio prodotto e togliamo il doppio prodotto.
Otteniamo così, mettendolo in evidenza con delle parentesi ad hoc, la differenza di due quadrati. |
Vediamo un altro esempio:
81a⁴ + 4b⁴ =
= (9a²)² + 36a²b² +(2b²)² – 36a²b² =
= [(9a²)² + 36a²b² +(2b²)²] – 36a²b² =
= (9a² + 2b²)² – (6ab)² =
=(9a² + 2b² + 6ab)(9a² + 2b² – 6ab)
= (9a²)² + 36a²b² +(2b²)² – 36a²b² =
= [(9a²)² + 36a²b² +(2b²)²] – 36a²b² =
= (9a² + 2b²)² – (6ab)² =
=(9a² + 2b² + 6ab)(9a² + 2b² – 6ab)
