GLI ANGOLI

Definizione

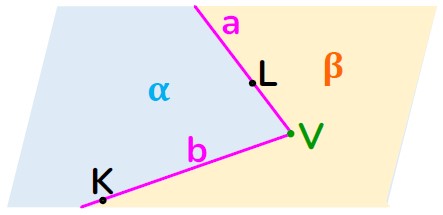
Un angolo è ciascuna delle due parti (α e β) di un piano individuate da due sue semirette aventi origine in comune, comprese le due semirette. ​

Le due semirette prendono il nome di lati dell’angolo, mentre l’origine delle due semirette è vertice dell’angolo.
In un angolo, dunque, sono sempre presenti:

• i lati, ciascuna delle due semirette a e b, o dei due lati LV e KV;
• il vertice, cioè il punto di origine delle due semirette o estremo in comune di due lati.

Tutti i punti appartenenti al piano ma non ai suoi lati sono interni all’angolo che li contiene.
Gli angoli si possono indicare in diversi modi:

• con le lettere minuscole dell’alfabeto greco (α, β, …);
• indicando i suoi lati (ab, ba, …);
• indicando un punto appartenente al primo lato, il vertice e un punto appartenente al secondo lato (KVL, KVL …).

In generale le due semirette viste sopra formano due tipologie di angoli:

Tipo di angolo	convesso	concavo
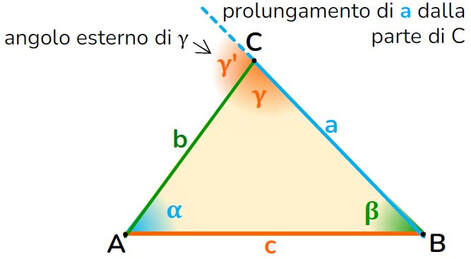
prolungamento dei lati	non li contiene	li contiene
ampiezza dell'angolo	minore di 180°	maggiore di 180°

---

La misura degli angoli in gradi sessagesimali

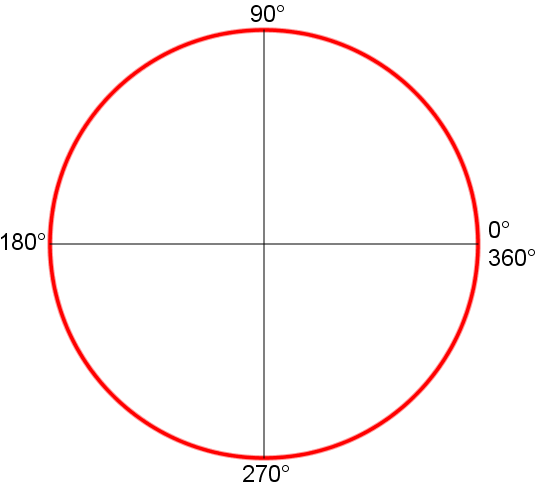
Un angolo giro, cioè l'ampiezza che riempie tutto il piano, corrisponde a 360°.
1° = 60'             un grado è uguale a 60 primi
1' = 60"             un primo è uguale a 60 secondi
1° = 60' = 360"      un grado è uguale a 60 primi

Ricorda: 
1° = 60' = 59' 60''
90° = 89° 60' = 89° 59' 60''

Questo è davvero importante quando dovrai sottrarre a misure angolari espresse solo in gradi, altre misure angolari espresse in gradi primi e secondi.

---

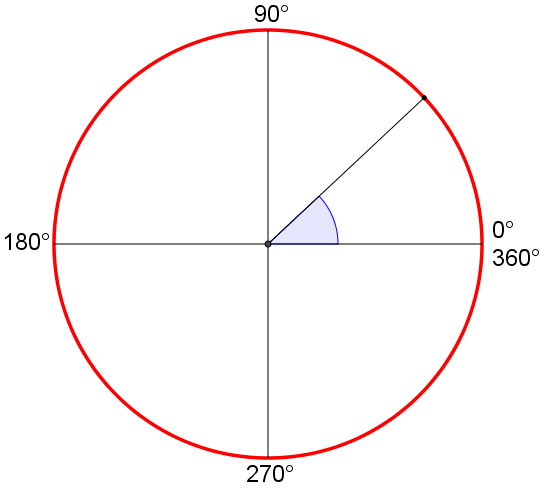
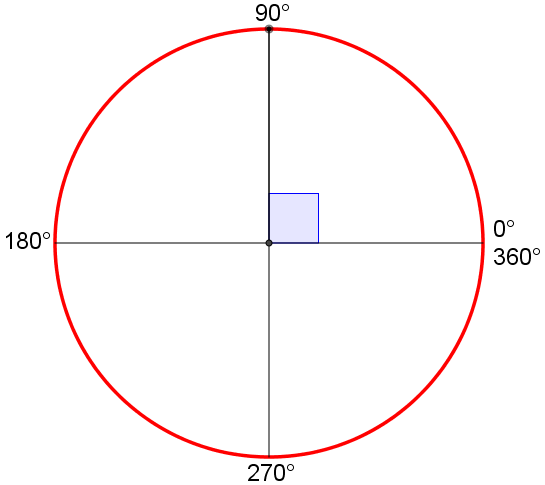
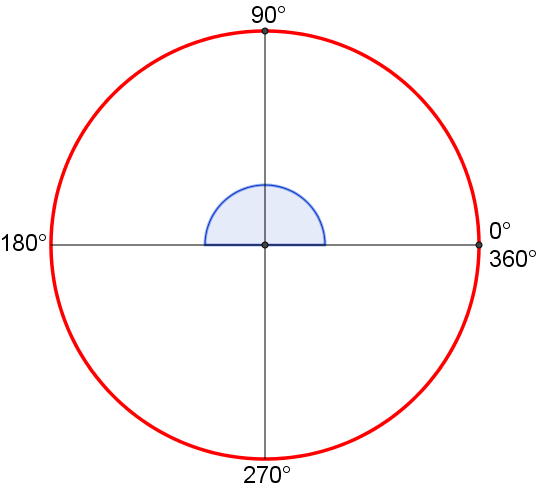
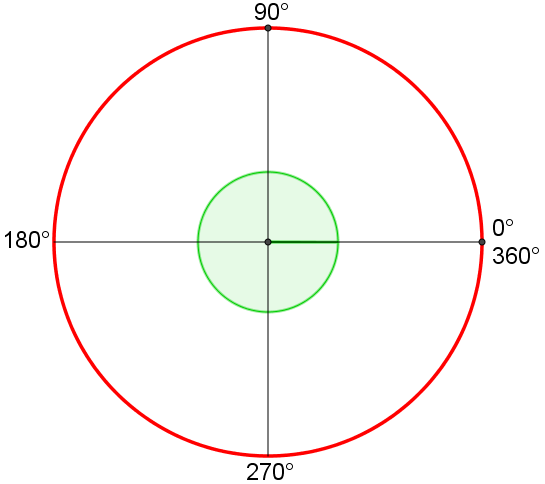
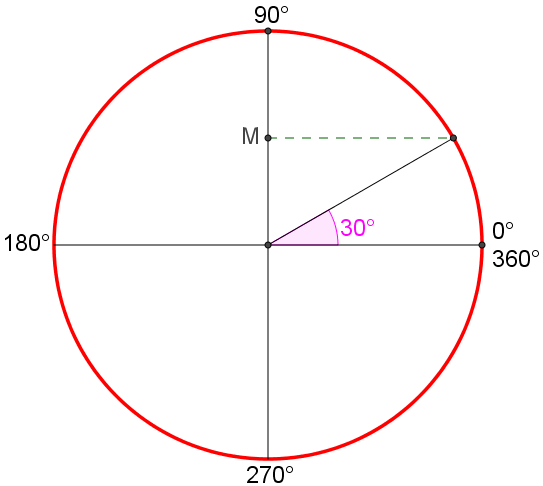
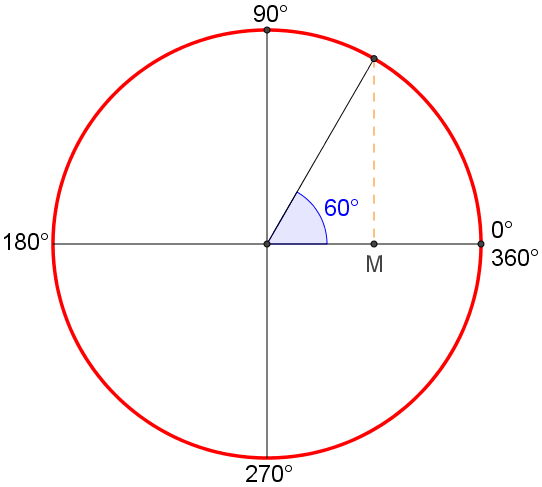
Classificazione degli angoli rispetto alla loro misura in gradi

Animazione con Geogebra

Angolo nullo = 0°

0° < angolo acuto < 90°

Angolo retto = 90°

---

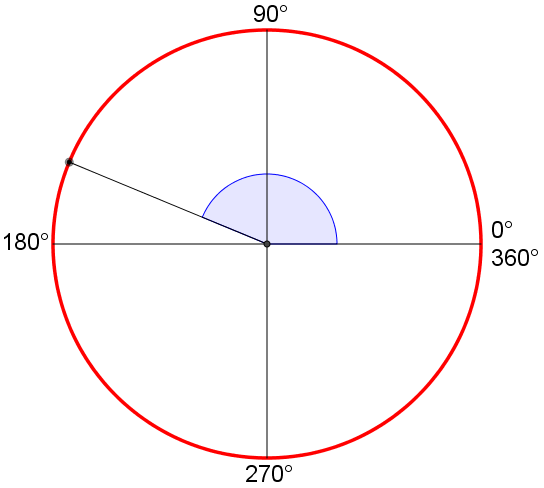
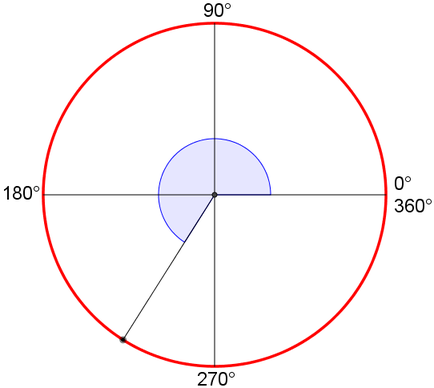
90° < a. ottuso < 180°

Angolo piatto = 180°

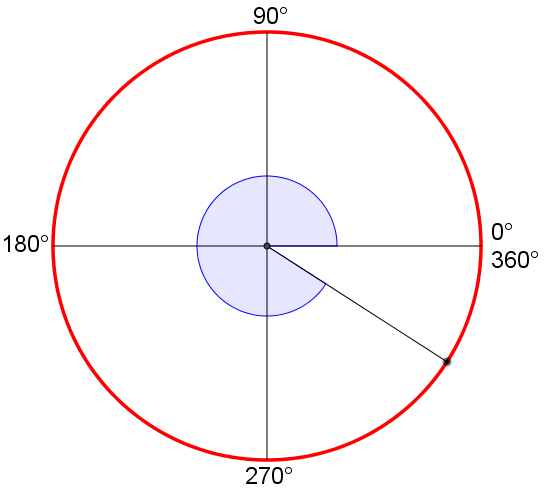
180° < a. concavo < 360°

---

---

180° < angolo concavo < 360°
​180° < reflex angle < 360°

Angolo giro = 360°
​Full circle = 360°

---

Angoli particolari

Relazione tra due angoli

Angoli consecutivi, adiacenti e opposti al vertice

In queste relazioni viene considerata la posizione reciproca degli angoli. 
In tutti i casi gli angoli hanno sempre in comune il vertice.

Angoli consecutivi

Angoli adiacenti

Angoli opposti al vertice

​Hanno un lato e il vertice in comune.

Sono consecutivi e i lati non in comune giacciono sulla stessa retta e stanno su parti opposte

Lo si dice di due angoli, uno di fronte all'altro, formati da due rette incidenti

---

Angoli complementari, supplementari e esplementari

Nelle seguenti relazioni è stata presa in considerazione la somma di due angoli. 
In molti poligoni alcuni angoli formano somme speciali: 90°, 180° e 360°.
Da qui la necessità di dare a queste somme dei nomi specifici.

Angoli complementari

Angoli supplementari

Angoli esplementari

Si dice di due angoli
la cui somma
​è un angolo retto
α + β = 90°

Si dice di due angoli
la cui somma
​è un angolo piatto
​α + β​ = 180°

Si dice di due angoli
la cui somma
è un angolo giro
α + β = 360°

Angoli interni e angoli esterni

Angolo interno → quella porzione di piano compresa tra due lati consecutivi e che è contenuto nella figura.

Angolo esterno → in un poligono convesso (dove ciascun angolo interno è sempre minore di un angolo piatto) è quell’angolo adiacente all’angolo interno, dunque è ad esso supplementare (insieme formano un angolo piatto).

L’angolo esterno ha in comune con il corrispondente angolo interno un lato e il prolungamento dell’altro lato.

​Per ogni angolo interno esistono due angoli esterni.

---

Rette tagliate da una trasversale

Rette parallele tagliate da una trasversale

Costruire la bisettrice di un angolo

contatore inserito il 23 agosto 2021