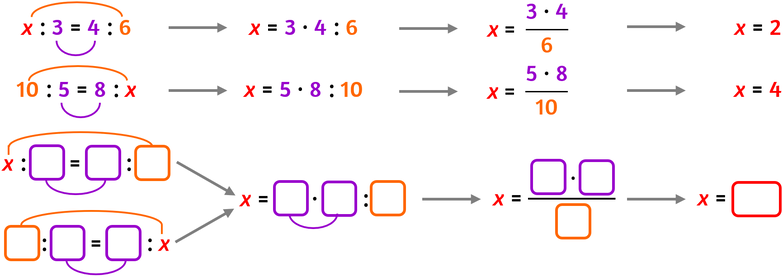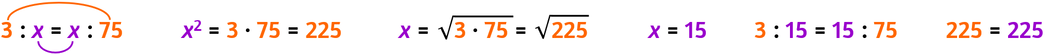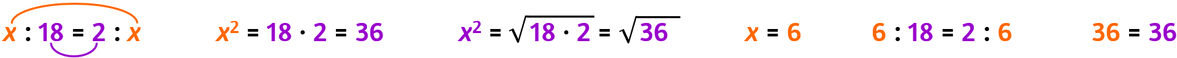LE PROPORZIONI
Che cos'è una proporzione
|
Vediamo ora due esempi nei quali si mette in evidenza una relazione tra due quantità numeriche:
|
|
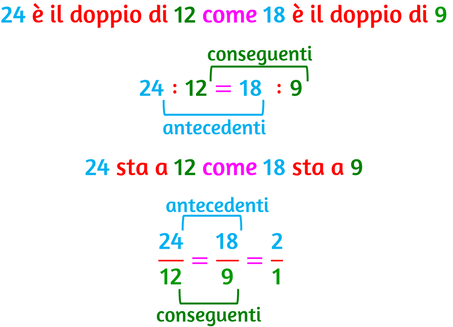
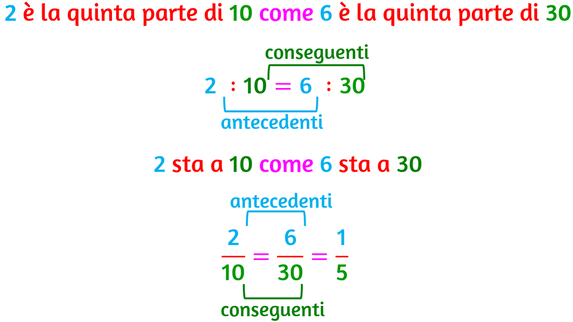
In entrambi gli esempi si uguagliano le relazioni tra le due coppie di numeri:
- nel primo caso la relazione tra i due numeri è che uno è il doppio dell'altro;
- nel secondo caso la relazione tra i due numeri è che uno è la quinta parte dell'altro.
Si chiama proporzione l'uguaglianza di due rapporti
(tra le coppie di numeri esiste sempre la stessa relazione).
(tra le coppie di numeri esiste sempre la stessa relazione).
Essendo il rapporto la relazione tra due numeri divisi tra loro (divisione o frazione), ne consegue che entrambe le scritture sopra sono equivalenti.
Video Teoria - Le proporzioni - definizione
Medi, estremi e la proprietà fondamentale
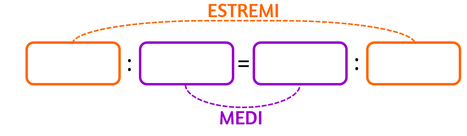
In una proporzione si chiamano:
- medi → i termini vicini al segno di uguale
- estremi → i termini distanti dal segno di uguale
- quarto proporzionale → l'ultimo termine di una proporzione.
Ho scelto:
- un sorriso 😃 tra i medi (i termini vicini al segno di uguale) in quanto si vogliono bene e sono felici perché sono vicini;
- una faccina triste 😟 tra gli estremi perché nonostante la distanza si vogliono bene, ma sono distanti e quindi sono tristi.
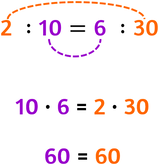
Ricapitolando, in ogni proporzione:
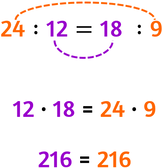
Per avvalorare la seconda, invece, si scrivono i due rapporti come divisioni, dopodiché si uniscono con una linea i medi e con un'altra linea gli estremi
- il valore del primo rapporto deve essere uguale al rapporto del secondo rapporto;
- il prodotto dei medi deve essere uguale al prodotto degli estremi.
Per avvalorare la seconda, invece, si scrivono i due rapporti come divisioni, dopodiché si uniscono con una linea i medi e con un'altra linea gli estremi
|
La proprietà fondamentale
dice che il prodotto dei medi è uguale al prodotto degli estremi. |
|
|
Calcolo del termine incognito
Se in una proporzione si conoscono 3 dei suoi termini è possibile conoscere il valore del quarto termine non conosciuto (termine incognito).
Per prima cosa mettiamo in evidenza i medi e gli estremi con due linee che li uniscono.
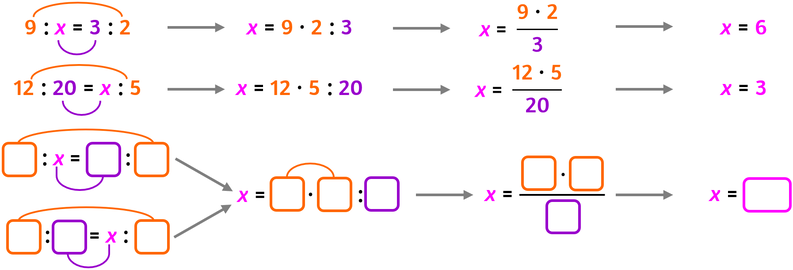
Se l'incognita è un estremo:
- moltiplico i medi;
- divido il risultato per l'estremo conosciuto
Se l'incognita è un medio:
- moltiplico gli estremi;
- divido il risultato per il medio conosciuto
Le proporzioni continue
Una proporzione si dice continua quando i medi o gli estremi sono uguali.
Se i termini uguali sono i medi si parla di medio proporzionale.
Se i termini uguali sono gli estremi si parla di estremo proporzionale.
Se i termini uguali sono gli estremi si parla di estremo proporzionale.
In una proporzione continua il valore dei due termini incogniti è uguale alla radice quadrata del prodotto dei due termini noti.
Il valore del medio proporzionale = estrazione della radice quadrata del prodotto degli estremi.
Il valore dell’estremo proporzionale = estrazione della radice quadrata del prodotto dei medi.
Proprietà dell'invertire e del permutare
PROPRIETÀ DELL'INVERTIRE
Se scambi di posto ogni antecedente con il proprio conseguente ottieni una nuova proporzione.
Questo perché se i rapporti diretti hanno lo stesso valore, avranno lo stesso valore anche i rispettivi rapporti inversi.
Questo perché se i rapporti diretti hanno lo stesso valore, avranno lo stesso valore anche i rispettivi rapporti inversi.
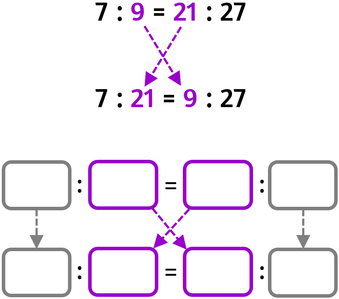
PROPRIETÀ DEL PERMUTARE
Se scambi di posto tra loro i medi, o gli estremi o sia i medi sia gli estremi, ottieni sempre una nuova proporzione.
Questo perché dalla proprietà fondamentale sappiamo che in una proporzione il prodotto dei medi è uguale al prodotto degli estremi, ne consegue che se scambiamo di posto i medi tra loro e/o gli estremi tra loro, il prodotto rimane comunque invariato.
Questo perché dalla proprietà fondamentale sappiamo che in una proporzione il prodotto dei medi è uguale al prodotto degli estremi, ne consegue che se scambiamo di posto i medi tra loro e/o gli estremi tra loro, il prodotto rimane comunque invariato.
|
Permutare i medi |
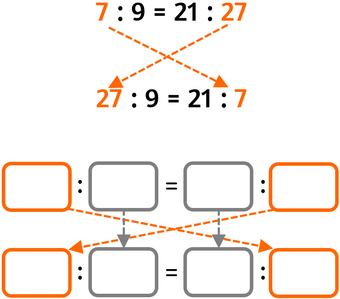
Permutare gli estremi |
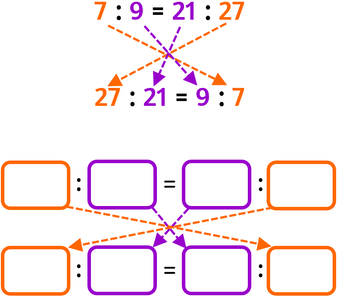
Permutare
sia i medi che gli estremi |
|
|
|
Quando applichi la proprietà del permutare sia i medi sia gli estremi, la nuova proporzione corrisponde a quella originale scritta completamente al contrario.
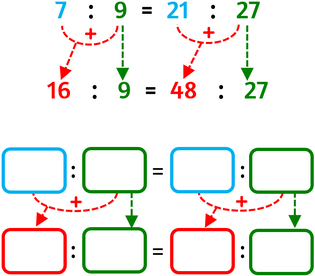
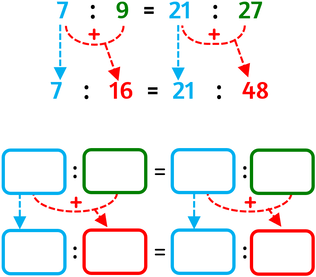
PROPRIETÀ DEL COMPORRE
Applicando la proprietà del comporre ottieni una nuova proporzione sostituendo a entrambi gli antecedenti o a entrambi i conseguenti la somma «antecedente + conseguente» di uno stesso rapporto:
|
|
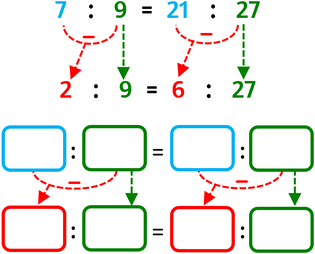
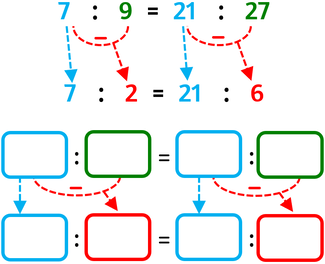
PROPRIETÀ DELLO SCOMPORRE
Applicando la proprietà dello scomporre ottieni una nuova proporzione sostituendo a entrambi gli antecedenti (o a entrambi i conseguenti) la differenza possibile «antecedente – conseguente» (oppure «conseguente – antecedente») sempre di uno stesso rapporto.
|
|
LE CATENE DI RAPPORTI
Si chiama catena di rapporti l’uguaglianza di tre o più rapporti.
5 : 8 = 15 : 24 = 2,5 : 4 = 10 : 16 = … : …
E se alcuni di essi sono incogniti e solo uno è noto?
4 : 3 = x : 9 = y : 1,5 = z : 21
Per trovare i valori incogniti eguaglia il rapporto noto con ciascun rapporto in cui compare l’incognita.
Poiché l’incognita occupa la posizione di un medio, troverai il suo valore dividendo il prodotto degli estremi per il medio conosciuto:
Poiché l’incognita occupa la posizione di un medio, troverai il suo valore dividendo il prodotto degli estremi per il medio conosciuto:
|
4 : 3 = x : 9
x = 4 · 9 : 3 = 12 |
4 : 3 = y : 1,5
y = 4 · 1,5 : 3 = 2 |
4 : 3 = z : 21
z = 4 · 21 : 3 = 28 |
Le catene di rapporti e la proprietà del comporre
E se ogni rapporto ha un incognita ma conosciamo il valore della somma delle incognite?
x : 5 = y : 3 = z : 7 → x + y + z = 120
Per prima cosa aggiungi alla catena di rapporti il rapporto:
«somma di tutti gli antecedenti» : «somma di tutti i conseguenti»
«somma di tutti gli antecedenti» : «somma di tutti i conseguenti»
x : 5 = y : 3 = z : 7 = (x + y + z) : (5 + 3 + 7)
Sostituisci alle due somme i loro valori.
x : 5 = y : 3 = z : 7 = 120 : 15
Ora hai puoi calcolare i valori incogniti eguagliando ciascun rapporto con un termine incognito al rapporto noto.
In ogni proporzione lega tra loro i medi e gli estremi, il valore dell’incognita sarà uguale al prodotto dei medi diviso l’estremo conosciuto.
In ogni proporzione lega tra loro i medi e gli estremi, il valore dell’incognita sarà uguale al prodotto dei medi diviso l’estremo conosciuto.
x : 5 = 120 : 15 → x = 5 · 120 : 15 = 40
y : 3 = 120 : 15 → y = 3 · 120 : 15 = 24
z : 7 = 120 : 15 → z = 7 · 120 : 15 = 56
y : 3 = 120 : 15 → y = 3 · 120 : 15 = 24
z : 7 = 120 : 15 → z = 7 · 120 : 15 = 56
| 3_ppt_aritmetica_6le_proporzioni.ppsx |
Video Teoria - Le proporzioni - definizione
Video Teoria - La proprietà fondamentale e sue applicazioni
Video Esercizio - Verificare se una sequenza di 4 numeri forma una proporzione
Video Esercizio - Calcolo del termine incognito in una proporzione
Video Teoria - La proprietà fondamentale e sue applicazioni
Video Esercizio - Verificare se una sequenza di 4 numeri forma una proporzione
Video Esercizio - Calcolo del termine incognito in una proporzione
|
|
Contatore inserito il 12 luglio 2021
|