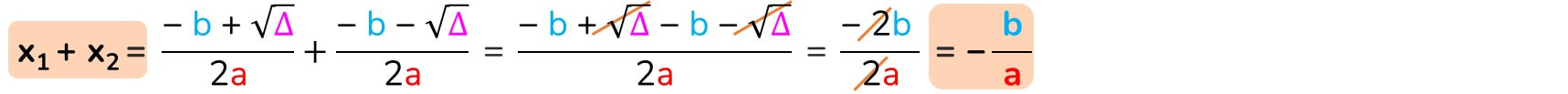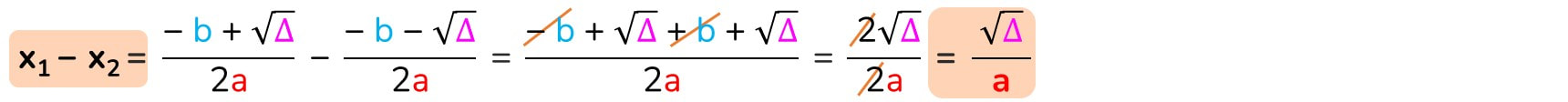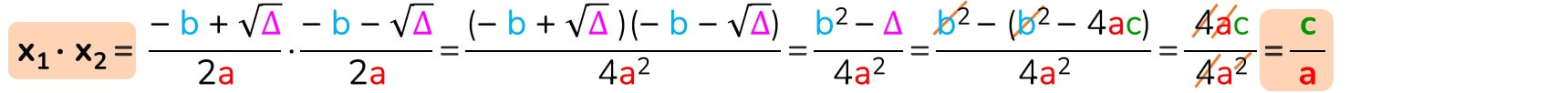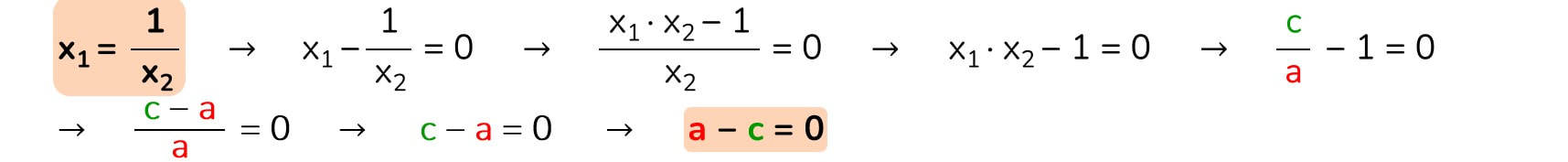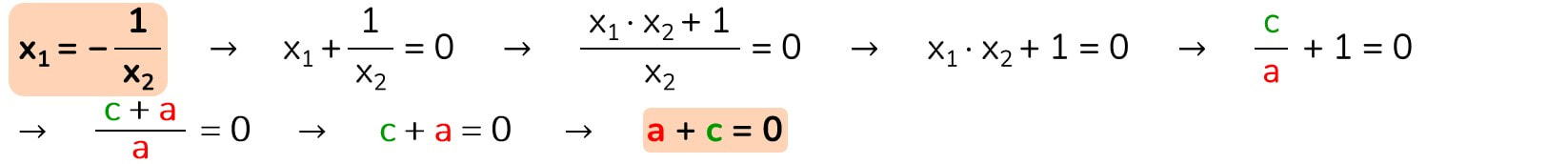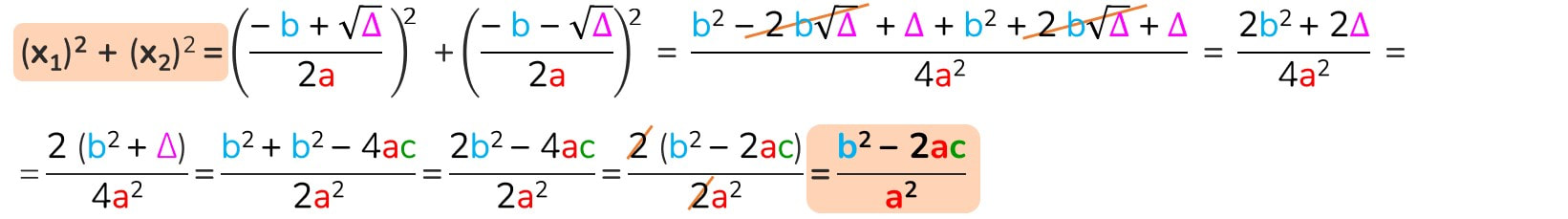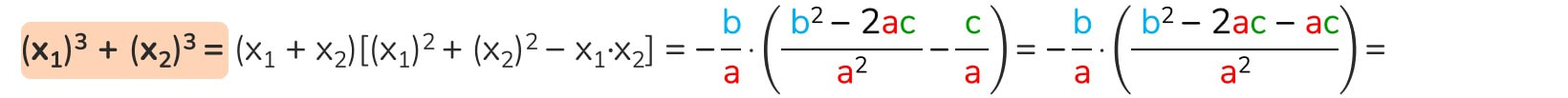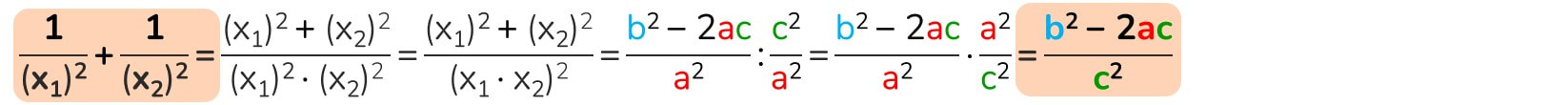EQUAZIONI PARAMETRICHE DI SECONDO GRADO
Traduzione delle frasi presenti nei problemi
Positivo → maggiore di zero → > 0
Negativo → minore di zero → < 0
Le radici sono reali: stabilisci quando il ∆ ≥ 0 → b² – 4ac ≥ 0
Le radici NON sono reali: stabilisci quando il ∆ < 0
Le radici sono reali e distinte: stabilisci quando il ∆ > 0
Le radici sono reali e coincidenti: stabilisci quando il ∆ = 0 → si tratta del quadrato di un binomio.
Una radice è uguale a zero → quando l’equazione è spuria → quando il coefficiente c = 0
Una radice è nulla → quando l’equazione è spuria → quando il coefficiente c = 0
Una radice è nulla → quando l’equazione è spuria → quando il coefficiente c = 0
Una radice è uguale a …
- determina per quali valori del parametro l’equazione ammette radici reali;
- sostituisci all’incognita x dell’equazione il valore dato e risolvi ora l’equazione nell’incognita parametrica.
La somma delle radici è uguale a ...
La somma delle radici è positiva
La somma delle radici è uguale a zero
Se la somma delle due radici è uguale a zero vuol dire che le due radici sono opposte e questo accade quando l'equazione è pura e ammissibile nell'ambito dei numeri reali (siamo di fronte al prodotto di una somma per una differenza).
Se la somma delle due radici è uguale a zero vuol dire che le due radici sono opposte e questo accade quando l'equazione è pura e ammissibile nell'ambito dei numeri reali (siamo di fronte al prodotto di una somma per una differenza).
- calcola il discriminate e imponilo maggiore o uguale a zero (soluzioni reali);
- infine imponi b = 0.
La differenza delle radici è uguale a ...
La differenza delle radici è uguale a zero
Se la differenza delle radici è uguale a zero vuol dire che x1 = x2, cioè le due radici sono reali e coincidenti e questo accade quando il discriminante è uguale a zero, cioè quando b² - 4ac = 0, siamo di fronte al quadrato di un binomio.
Se la differenza delle radici è uguale a zero vuol dire che x1 = x2, cioè le due radici sono reali e coincidenti e questo accade quando il discriminante è uguale a zero, cioè quando b² - 4ac = 0, siamo di fronte al quadrato di un binomio.
Il prodotto delle radici è uguale a ...
Le radici sono opposte
Se le radici sono opposte vuol dire che la loro somma è uguale a zero vuol dire e questo accade quando l'equazione è pura e ammissibile nell'ambito dei numeri reali (siamo di fronte al prodotto di una somma per una differenza).
Se le radici sono opposte vuol dire che la loro somma è uguale a zero vuol dire e questo accade quando l'equazione è pura e ammissibile nell'ambito dei numeri reali (siamo di fronte al prodotto di una somma per una differenza).
- calcola il discriminate e imponilo maggiore o uguale a zero (soluzioni reali);
- infine imponi b = 0.
Le radici sono reciproche
Due numeri si dicono reciproci quando uno, scritto sotto forma di frazione, è uguale all'inverso dell'altro: 2/3 è reciproco di 3/2; 7/11 è inverso di 11/7; 2 è inverso di 1/2 e 1/8 è inverso di 8.
Quando due numeri sono reciproci allora il loro prodotto è uguale a 1.
Nella dimostrazione che segue non si tiene conto di questa deduzione che però emerge nel terzo passaggio (se il prodotto è uguale a 1, la differenza tra il prodotto di due numeri reciproci e 1 dà come risultato zero).
Due numeri si dicono reciproci quando uno, scritto sotto forma di frazione, è uguale all'inverso dell'altro: 2/3 è reciproco di 3/2; 7/11 è inverso di 11/7; 2 è inverso di 1/2 e 1/8 è inverso di 8.
Quando due numeri sono reciproci allora il loro prodotto è uguale a 1.
Nella dimostrazione che segue non si tiene conto di questa deduzione che però emerge nel terzo passaggio (se il prodotto è uguale a 1, la differenza tra il prodotto di due numeri reciproci e 1 dà come risultato zero).
Le radici sono antireciproche
La somma dei reciproci delle radici è uguale a ...
La somma dei quadrati delle radici è uguale a ...
La somma dei cubi delle radici è uguale a ...
La somma dei quadrati dei reciproci delle radici è uguale a ...
Il prodotto dei reciproci delle radici è uguale a ...