Caratteristiche dei polinomi
Si chiama polinomio quell'espressione letterale nella quale compaiono monomi simili e/o non simili sommati o sottratti tra loro.
Sono esempi di polinomi:
ax² |
3a + 7 – 4ab + 12a |
7x + 4y |
3 |
b³ – 2by + y⁵ |
da questo si evince che anche ogni monomio è un polinomio.
Ciascun monomio che compone il polinomio prende il nome di termine del polinomio.
Il termine che non possiede una parte letterale prende il nome di termine noto del polinomio.
Il termine che non possiede una parte letterale prende il nome di termine noto del polinomio.
13a⁶x + 7 a⁴b³ – 4x²y⁵ – 21
|
Il polinomio sopra è composto da 4 termini (quadrinomio) e il termine noto è –21.
Il termine noto si chiama in questo modo perché è quel termine del quale si conosce essattamente il suo valore, dunque è noto (conosciuto)monomio, in quanto non accompagnato da nessuna lettera.
In alcuni polinomi possono comparire lettere che nella realtà sono termini noti: come il π che pur essendo una lettera ha un valore ben definito (π = pi-greco = 3,14159265...)
Polinomio in forma normale
Un polinomio è ridotto in forma normale quando non sono presenti monomi simili, cioè quando non è più possibile semplificare monomi tra loro. |
3a + 7 – 4ab + 12a
non è ridotto in forma normale
(3 + 12)a + 7 – 4ab =
= 15a + 7 – 4ab
polinomio ridotto in forma normale
non è ridotto in forma normale
(3 + 12)a + 7 – 4ab =
= 15a + 7 – 4ab
polinomio ridotto in forma normale
Dalla quantità di termini nel polinomio a un nome specifico
Un polinomio, ridotto in forma normale (privo di monomi simili), formato da un massimo di 4 termini viene chiamato monomio, binomio, trinomio e quadrinomio a seconda dei termini cui è composto.
Polinomio formato da: |
Il polinomio si chiama: |
Esempi |
1 termine |
monomio |
a⁵ –3 4a²b⁵y⁷ |
2 termini |
binomio |
x² + y³ 4a – 8b |
3 termini |
trinomio |
b² – 2by + y² ax + by +c |
4 termini |
quadrinomio |
x³ – 3x²y + 3xy² – y³ |
Grado di un polinomio
In un polinomio, ridotto in forma normale, si ha che:
- il grado di un polinomio rispetto ad una lettera è rappresentato dal più grande esponente posseduto dalla lettera nel polinomio;
- il grado di un polinomio è rappresentato dal grado massimo posseduto da uno dei termini che lo compongono.
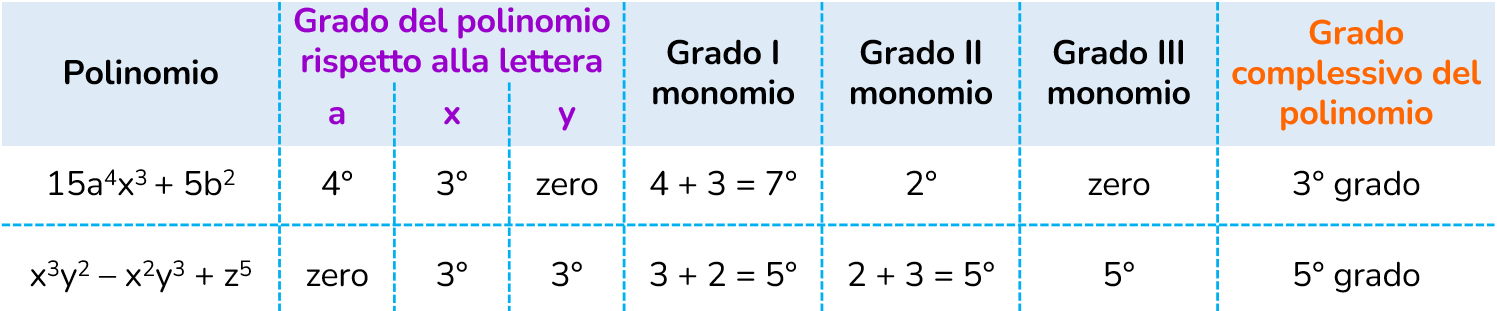
Calcola il grado del seguente polinomio:
4a²xy³ + 5ax – 15a³y
Calcola il grado di ciascun monomio sommando gli esponenti di tutte le lettere presenti (ricorda, se una lettera non ha esponente è sottinteso 1):
4a²xy³ → grado: 2 + 1 + 3 = 6°
+ 5ax → grado: 1 + 1 = 2°
–15 a³y → grado: 3 + 1 = 4°
+ 5ax → grado: 1 + 1 = 2°
–15 a³y → grado: 3 + 1 = 4°
Infine posso affermare che il grado del polinomio è uguale a 6, perché è il più alto grado posseduto da uno dei monomi che lo compongono.
Polinomi omogenei, ordinati e completi
Polinomio omogeneo
Un polinomio, ridotto in forma normale, si dice omogeneo quando tutti i monomi che lo compongono hanno lo stesso grado.
13a⁶x + 7a⁴b³ – 4x²y⁵
La somma degli esponenti delle lettere in ciascun monomio è 7 = 6 + 1 = 4 + 3 = 2 + 5.
Polinomio ordinato
Un polinomio, ridotto in forma normale, si dice ordinato, rispetto ad una sua lettera, quando gli esponenti della lettera, leggendo i termini del polinomio da sinistra verso destra, sono disposti in ordine crescente o decrescente.
22a⁴y – 4a²xy³ + 5ax
Nell'esempio sopra il polinomio è ordinato secondo le potenze decrescenti di a.
13a⁶x + 7a⁴ + ax³ – 4a² + a⁵
Nell'esempio sopra il polinomio NON è ordinato secondo le potenze di a, in quanto nel leggere il polinomio da sinistra verso destra le potenze di a sono 6 - 4 - 1 - 2 - 5 e non sono ordinate.
Polinomio completo
Un polinomio si dice completo, rispetto ad una lettera, quando dopo averlo ordinato gli esponenti di quella lettera compaiono tutti dal maggiore al minore o viceversa, compreso il termine noto (che sarà il grado zero per la lettera considerata).
31a³x + 7a²x³ – 4ax² – 21x⁴
Nell'esempio sopra il polinomio è sia completo che ordinato secondo la lettera a, infatti andando da sinistra verso destra i suoi esponenti sono 3 - 2 - 1 - 0 (0 quando la lettera a è mancante), mentre per la lettera x non è completo perché i suoi esponenti sono 1 - 3 - 2 - 4 in quanto e tutti i termini del polinomio hanno la lettera x e non c'é un termine senza lettera x.
Polinomi uguali e polinomi opposti
Polinomi uguali
Due o più polinomi, ridotti in forma normale, sono uguali quando hanno lo stesso numero di termini e i termini del primo polinomio, indipendentemente dall’ordine in cui compaiono, compaiono identici nel secondo polinomio.
22a⁴y – 4a²xy³ + 5ax e 5ax + 22a⁴y – 4a²xy³
sono due polinomi uguali, entrambi i polinomi sono formati da 3 termini e ciascun termine del primo polinomio compare nel secondo polinomio.
Polinomi opposti
Due polinomi, ridotti in forma normale, si dicono opposti quando hanno lo stesso numero di termini e i termini del primo polinomio, indipendentemente dall’ordine in cui compaiono, sono opposti a quelli del secondo polinomio.
13a⁶x + 7a⁴ – ax³ – 4a² + a⁵ e – 7a⁴ + 4a² – a⁵ + ax³ – 13a⁶x
sono due polinomi opposti, entrambi i polinomi sono formati da 5 termini e ciascun termine del primo polinomio compare cambiato di segno nel secondo polinomio.
Polinomi come funzioni e zeri del polinomio
Essendo un polinomio un’espressione nella quale compaiono delle lettere, queste possono essere trattate come delle variabili.
I polinomi si indicano con le lettere maiuscole dell’alfabeto e tra parentesi si indicano le variabili che compaiono.
I polinomi si indicano con le lettere maiuscole dell’alfabeto e tra parentesi si indicano le variabili che compaiono.
P(a, x) = 13a⁶x + 7a⁴ – ax³ – 4a² + a⁵ → compaiono le lettere a e x
P(x) = x³ – x² + x – 21 → compare solo la lettera x
È possibile calcolare il valore di un polinomio, sostituendo alla variabile, o alle variabili, il/i valore/i che decidi o ti viene chiesto di attribuire.
Supponi di avere il polinomio: P(x) = x³ – x² + x – 21
e di voler calcolare il suo valore quando la x = – 1 e quando la x = 3, vedi cosa succede:
e di voler calcolare il suo valore quando la x = – 1 e quando la x = 3, vedi cosa succede:
P(–1) = (–1) ³ – (–1)² + (–1) – 21 = – 1 – 1 – 1 – 21 = – 25
P(3) = 3³ – 3² + 3 – 21 = 27 – 9 + 3 – 21 = 30 – 30 = 0
Nel caso in cui sostituisci alla variabile x il valore di – 1, ottieni che il polinomio ha valore – 25.
Nel caso in cui sostituisci alla variabile x il valore di 3, ottieni che il polinomio ha valore 0.
Nel caso in cui sostituisci alla variabile x il valore di 3, ottieni che il polinomio ha valore 0.
Quando un numero, sostituito alla variabile, rende zero il valore del polinomio, allora si dice che quel numero è uno zero del polinomio o una radice del polinomio.