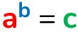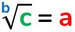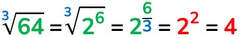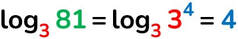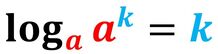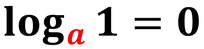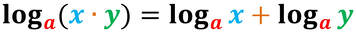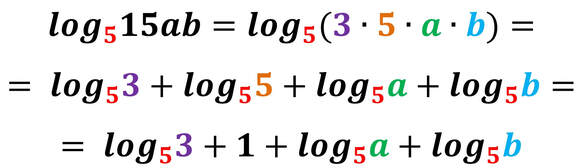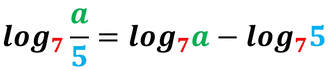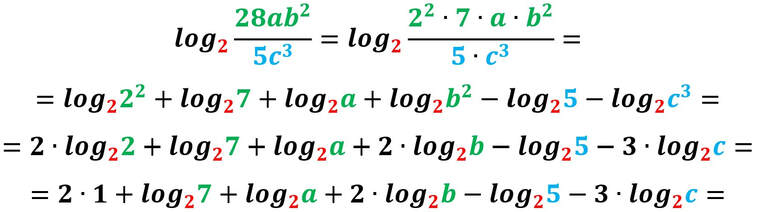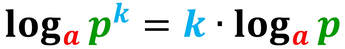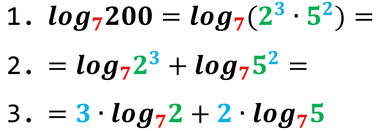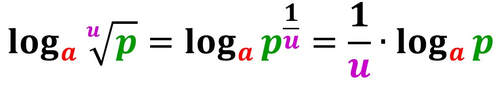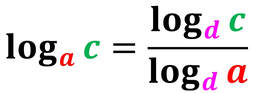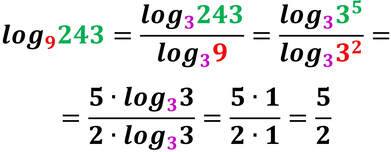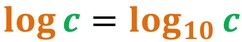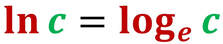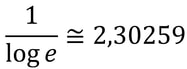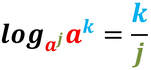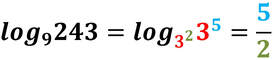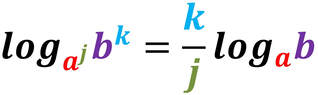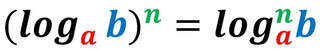I logaritmi

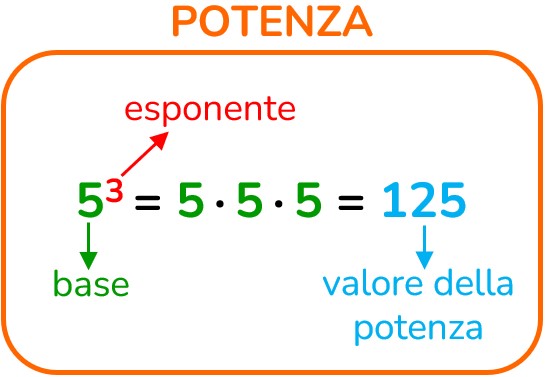
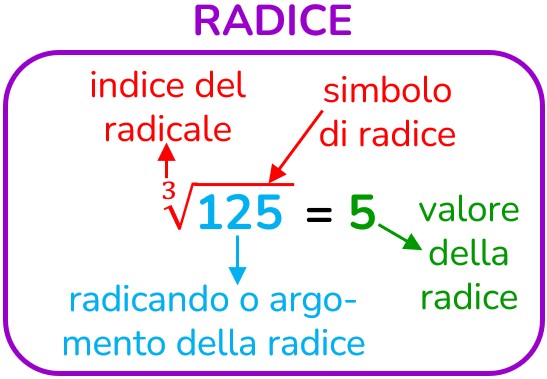
Sino ad ora abbiamo visto che l'operazione inversa dell'elevamento a potenza era la radice. 
Nelle radici di indice uguale all'esponente della potenza, la radice è rappresentata dalla base della potenza.
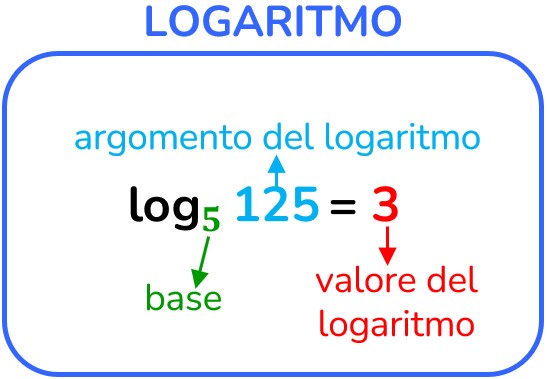
Ma, talvolta è importante conoscere qual è l'esponente che è stato dato ad una certa base per ottenere la potenza stessa. Questo è il compito del logaritmo.
​Facciamo un pochino di ripasso:

Le potenze

Si chiama potenza quel numero c che otteniamo moltiplicando per sé stesso un numero a qualunque, quante volte lo dice l'esponente b.

Come trovo il valore della potenza 2⁵?
Moltiplicando per sé stesso il 2 per 5 volte.

I radicali

Si chiama radicale di indice b della quantità c quel numero a che rappresenta la base di una potenza che ha come esponente b.

Come trovo il valore della radice cubica di ?

1. Scompongo in fattori primi il 64
2. Divido l’esponente di ciascuna potenza per l’indice della radice 

I logaritmi

Si chiama logaritmo l'esponente che devo dare alla base del logaritmo per ottenere l'argomento del logaritmo stesso.
Il logaritmo è così l'esponente b che devo dare alla base a per ottenere la potenza c. 

Qual è l’esponente che devo dare alla base 3 per ottenere l’argomento 81?
​È 4, infatti 3⁴ = 81

---

PROPRIETÀ DEI LOGARITMI

Trovare un logarigmo vuol dire trovare l'esponente da dare alla base del logaritmo per ottenere l'argomento. 

Logaritmo in cui base del logaritmo e argomento sono potenze che hanno la stessa base

Se l'argomento di un logaritmo è una potenza che ha come base la stessa base del logaritmo, l’esponente della potenza è il valore del logaritmo.

Per definizione: che esponente devo dare a 3 per ottenere il valore di 3⁴?

---

Logaritmo avente base e argomento uguali

Se un logaritmo ha come argomento la base del logaritmo, il valore del logaritmo è 1.
Qualunque numero elevato 1 è uguale a sé stesso, ecco se base del logaritmo e argomento coincidono vuol dire che l’esponente sottinteso è 1.

---

Logaritmo con argomento 1

Se un logaritmo ha come argomento 1, qualunque sia la base, il suo valore è 0, questo perché qualunque quantità elevata zero da come valore 1.

---

Logaritmo di un prodotto

Il logaritmo di un prodotto è uguale alla somma di logaritmi aventi tutti la stessa base e per argomento i singoli fattori del prodotto.
​​

Quando devo scomporre un logaritmo il cui argomento è un prodotto o può essere scomposto come prodotto, lo riscriviamo come somma di tanti logaritmi quanti sono i fattori che formano la scomposizione, tutti avranno la stessa base e come argomento ciascuno dei fattori della scomposizione.

---

Logaritmo di un quoziente

Il logaritmo di un quoziente (di una frazione o di una divisione) è uguale alla differenza di logaritmi aventi tutti la stessa base e per argomento i singoli fattori del prodotto.

Quando devo scomporre un logaritmo di un quoziente o una frazione, lo riscriviamo come differenza di logaritmi aventi la stessa base e come argomento ciascuno dei fattori della scomposizione.

Ricorda: tutto ciò che sta al numeratore deve essere sommato, tutto ciò che sta al denominatore deve essere sottratto.

---

Logaritmo di una potenza

Il logaritmo di una potenza è uguale al prodotto dell’esponente per il logaritmo della base.

1. Scomponi sempre l’argomento del logaritmo,
2. scomponi in somme di logaritmi
3. scrivi prima del logaritmo l’esponente dell’eventuale potenza

---

Logaritmo di un radicale

Il logaritmo di un radicale è uguale al a rapporto unitario con denominatore l’indice della radice moltiplicato il logaritmo del radicando. 

Ricorda:

Se il radicale è una potenza, avremo:

1. una frazione moltiplicata il logaritmo
2. la frazione ha come numeratore l’esponente della potenza, come denominatore l’indice della radice
3. il logaritmo avrà come argomento l'argomento del radicale privato dell'esponente 

Ricorda:

---

Trasformare un logaritmo in un altro avente diversa base

Per trasformare un logaritmo in un altro devo:

1. Scrivere una frazione tra due logaritmi aventi la nuova base (in genere io scelgo o il numero più piccolo, o il divisore comune)
2. Nel numeratore l’argomento sarà lo stesso del vecchio logaritmo;
3. Nel denominatore l’argomento sarà la base del vecchio logaritmo

Vediamo un esercizio, nel quale ho:

1. cercato un divisore comune tra la base e l'argomento del logaritmo
2. riscritto il logaritmo nella base del divisore comune
3. scomposto gli argomenti dei due logaritmi
4. trasportato fuori dal logaritmo l'esponente della potenza
5. semplificato a 1 tutti i logaritmi aventi base e argomento uguale.

---

Il logaritmo di base 10

Se nel logaritmo non è espressa la base,
​si sottintende 10 se è scritto come log.

---

Logaritmo naturale o neperiano

Il logaritmo naturale o logaritmo neperiano si scrive ln (l = logaritmo, n = naturale)

---

Logaritmo avente per base e argomento due potenze con la stessa base

Se base e argomento di un logaritmo sono due potenze aventi la stessa base, il valore del logaritmo è:

---

Logaritmo con base e argomento due potenze qualunque

Se la base e l'argomento di un logaritmo possono essere scritti (o lo sono già) come delle potenze, potremmo semplificare la scrittura come prodotto di una frazione per un nuovo logaritmo che avrà come nuovi argomenti e basi le basi delle potenze.

Avremo come risultato una frazione moltiplicato un logaritmo che avranno:

• ​numeratore della frazione: esponente del vecchio argomento
• denominatore della frazione: esponente del vecchio argomento
• argomento del logaritmo: base della potenza del vecchio argomento
• base del logaritmo: base della potenza della vecchia base del logaritmo

---

Potenza di un logaritmo

La potenza di un logaritmo è uguale al logaritmo elevato stesso esponente della stessa base e stesso argomento.

Quando ci si trova alla potenza di un logaritmo in una equazione occorre sostituire il logaritmo con una lettera qualunque e risolvere così l’equazione di grado superiore al primo.

---

contatore inserito il 22 maggio 2021