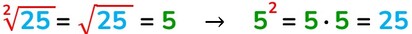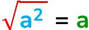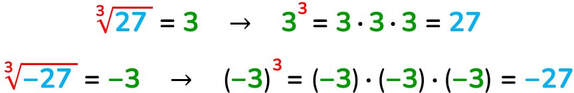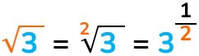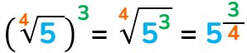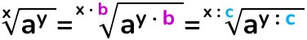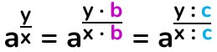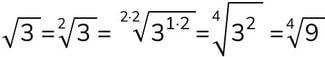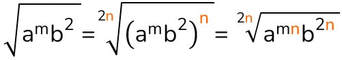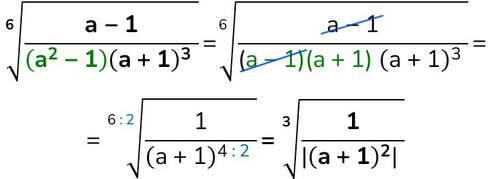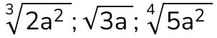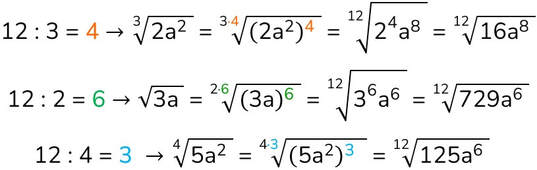L'OPERAZIONE DI RADICE E LE SUE OPERAZIONI INVERSE

L’operazione di radice è una delle operazioni inverse dell’elevamento a potenza.
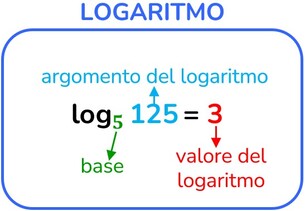
L’altra operazione inversa è il logaritmo.

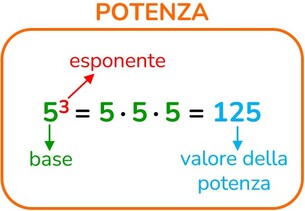
Potenza: qual è quel numero che ottieni moltiplicando la base per se stessa quante volte lo dice l’esponente?

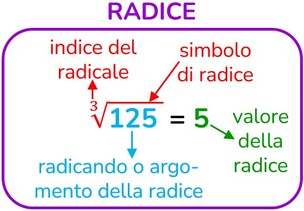
Radice: qual è quel numero che moltiplicato per se stesso quante volte lo dice l’indice della radice mi dà il radicando?

Logaritmo: quale esponente devo dare alla base del logaritmo per ottenere l’argomento?

LE RADICI QUADRATE

Si chiama radice quadrata di un numero reale quella quantità che elevata al quadrato dà come risultato l’argomento (o il radicando) della radice.

L’indice della radice può essere omesso quando questo è uguale a 2.

Si definiscono quadrati perfetti tutti quei numeri che si ottengono elevando al quadrato un numero naturale.
Qui di seguito vi propongo i primi 30 quadrati perfetti e al fianco di qualcuno un modo diverso per aiutare la memoria a ricordarli.

1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = ​100

11² = 10² + 21 · 1 = 121​
12² = 100 + 22 · 2 = 144
13² = 100 + 23 · 3 = 169
14² = 100 + 24 · 4 = 196
15² = 100 + 25 · 5 = 225
16² = 100 + 26 · 6 = 256
17² = 100 + 27 · 7 = 289
18² = 100 + 28 · 8 = 324
19² = 100 + 29 · 9 = 361
20² = (2 · 10)² = 4 · 100 = 400 

21² = 20² + 41 · 1 = 441
22² = 400 + 42 · 2 = 484
23² = 400 + 43 · 3 = 529
24² = 400 + 44 · 4 = 576
25² = 400 + 45 · 5 = 625
26² = 400 + 46 · 6 = 676
27² = 400 + 47 · 7 = 729
28² = 400 + 48 · 8 = 784
29² = 400 + 49 · 9 = 841
30² = ​(3 · 10)² = 9 · 100 = 900

I quadrati come il quadrato di un binomio
21² = (20 + 1)² → quadrato del primo + 2 · primo · secondo + quadrato del secondo 

11² = 10² + 2·10·1 + 1² = 100 + 20 + 1 = 121​
12² = 10² + 2·10·2 + 2² = 100 + 40 + 4 = 144
13² = 10² + 2·10·3 + 3² = 100 + 60 + 9 = 169
14² = 10² + 2·10·4 + 4² = 100 + 80 + 16 = 196
15² = 10² + 2·10·5 + 5² = 100 + 100 + 25 = 225
16² = 10² + 2·10·6 + 6² = 100 + 120 + 36 = 256
       = 20² – 2·20·4 + 4² = 400 – 160 + 16 = 256 
17² = 10² + 2·10·7 + 7² = 100 + 140 + 49 = 289
       = 20² – 2·20·3 + 3² = 400 – 120 + 9 = 289 
18² = 10² + 2·10·8 + 8² = 100 + 160 + 64 = 324
       = 20² – 2·20·2 + 2² = 400 – 80 + 4 = 324 
19² = 10² + 2·10·9 + 9² = 100 + 180 + 81 = 361
       = 20² – 2·20·1 + 1² = 400 – 40 + 1 = 361 
20² = (2 · 10)² = 4 · 100 = 400 

21² = 20² + 2·20·1 + 1² = 400 + 40 + 1 = 441
22² = 20² + 2·20·2 + 2² = 400 + 80 + 4 = 484
23² = 20² + 2·20·3 + 3² = 400 + 120 + 9 = 529
24² = 20² + 2·20·4 + 4² = 400 + 160 + 16 = 576
25² = 20² + 2·20·5 + 5² = 400 + 200 + 25 = 625
26² = 20² + 2·20·6 + 6² = 400 + 240 + 36 = 676
       = 30² – 2·30·4 + 4² = 900 – 240 + 16 = 676 
27² = 20² + 2·20·7 + 7² = 400 + 280 + 49 = 729
       = 30² – 2·30·3 + 3² = 900 – 180 + 9  = 729 
28² = 20² + 2·20·8 + 8² = 400 + 320 + 64 = 784
       = 30² – 2·30·2 + 2² = 900 – 120 + 4 = 784 
29² = 20² + 2·20·9 + 9² = 400 + 360 + 81 = 841
       = 30² – 2·30·1 + 1² = 900 – 60 + 1 = 841
30² = ​(3 · 10)² = 9 · 100 = 900

Si può estrarre la radice quadrata di un qualunque numero reale?

No. La radice quadrata esiste solo se l’argomento della radice è positivo o uguale a zero.
La radice di un numero negativo non esiste perché qualunque numero al quadrato dà come risultato un numero positivo.
È anche vero che qualunque numero al quadrato, sia esso positivo che negativo, dà come risultato un numero positivo per cui, mentre per una quantità numerica la radice quadrata è positiva, per una quantità letterale invece possono essere ammesse soluzioni apparentemente negative:

ma

a ∙ a = a²       e      (–a) ∙ (–a) = +a²

per cui

Condizioni di esistenza della radice quadrata

Una radice quadrata esiste, nell’insieme dei numeri reali ℝ, quando l’argomento è maggiore o uguale a zero. ​

LA RADICE CUBICA

Si chiama radice cubica di un numero reale ℝ quella quantità che elevata al cubo dà come risultato l’argomento della radice.
Diversamente dalla radice quadrata, quella cubica ammette sempre soluzioni sia positive che negative:

I NUMERI IRRAZIONALI E LE RADICI ENNESIME

Si chiamano numeri irrazionali quei valori di radici che hanno come caratteristica quella di essere un numero decimale illimitato e non periodico.
In linea generale i numeri razionali si esprimono come radici ennesime di numeri interi o razionali.
In generale le radici possono avere sia indice pari sia indice dispari: 

• se l'indice è dispari, l'argomento posto sotto il segno di radice, il radicando, può avere qualunque segno, sia positivo che negativo; 
• se l'indice è pari, l'argomento deve essere sempre positivo, e quindi maggiore o uguale a zero.

Si parla di radici n-esime (radici ennesime) tutte quelle radici che hanno come indice un quantità indefinita n.

• Se n = 1 → non esiste la radice quadrata → *
• Se n = 2 → si parla di radice seconda o radice quadrata, l’indice può essere omesso → **
• Se n = 3 → si parla di radice terza o radice cubica
• Se n = 4 → si parla di radice quarta
• Se n = 5 → si parla di radice quinta

CONDIZIONI DI ESISTENZA DEI RADICALI

L’esistenza dei radicali dipende esclusivamente da due fattori:

• dall’indice della radice;
• dal radicando.

Se l’indice della radice è:

• un numero naturale pari, allora il radicando deve essere maggiore o uguale a zero;
• un numero naturale dispari allora il radicando può essere qualunque numero reale.

​Ricorda: se il radicando è una frazione, imponi sempre il denominatore come diverso da zero. 

LE RADICI COME POTENZE

Qualunque radicale può essere visto come una potenza con indice razionale nella quale:

• l’indice della radice è il denominatore della frazione;
• l’esponente del radicale o del radicando è il numeratore della frazione.

Ne consegue che tutte le proprietà viste per le potenze possano essere applicate allo stesso modo per i radicali.

LA PROPRIETÀ FONDAMENTALE DEI RADICALI E SUA APPLICAZIONE

Proprietà fondamentale dei radicali

Si ottiene un radicale equivalente moltiplicando o dividendo sia l’indice del radicale sia l’esponente del radicando per una stessa quantità diversa da zero. ​

oppure

Grazie all’applicazione di questa proprietà è possibile riscrivere i radicali tutti con uno stesso indice, in questo modo sarà possibile semplificarli, confrontarli, moltiplicarli e/o dividerli.

Radicale irriducibile → quando indice del radicale e esponente del radicando sono primi tra loro. 

QUALCHE ESEMPIO SULL'APPLICAZIONE DELLA PROPRIETÀ FONDAMENTALE

Esempio numerico
​Moltiplico gli esponenti dell'argomento della radice e indice della radice per una stessa quantità diversa da zero.

Esempio algebrico
​Moltiplico gli esponenti dell'argomento della radice e indice della radice per una stessa quantità diversa da zero.

Esempio con le frazioni algebriche
Scomponi, riduci e metti insieme potenze con la stessa base

Condizioni di esistenza
Prima di semplificare le frazioni algebriche devi esplicitare le condizioni di esistenza, cioè devi imporre ciascun fattore del denominatore scomposto diverso da zero:
a − 1 ≠ 0 → a ≠ +1
a + 1 ≠ 0 → a ≠ −1

Ridurre più radicali allo stesso indice

Vediamo con un esempio come si procede. Riduci allo stesso indice i seguenti radicali: ​

1. calcola il mcm tra gli indici

mcm (3; 2, 4) = 12

2. dividi il mcm per ciascuno degli indici dei radicali e moltiplica il quoziente ottenuto sia per l’indice del radicale che per l’esponente del radicando

Operazioni coi radicali

Razionalizzazione

Contatore inserito il 22 maggio 2021