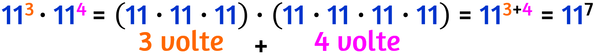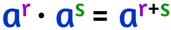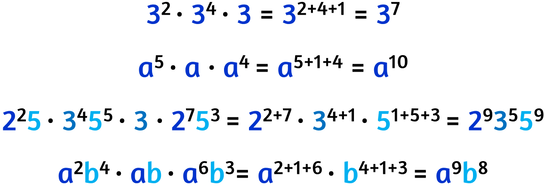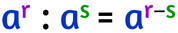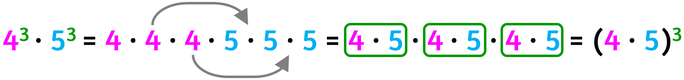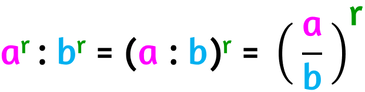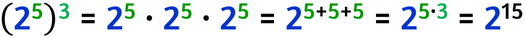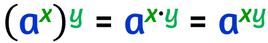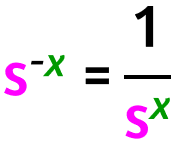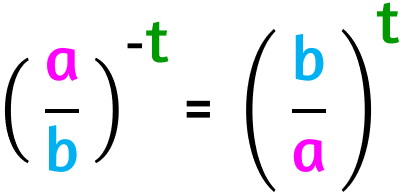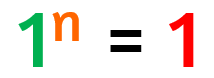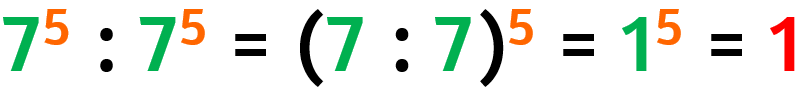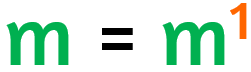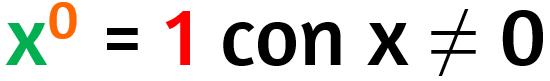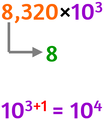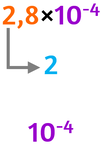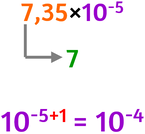PROPRIETÀ DELLE POTENZE E OPERAZIONI CON LE POTENZE
Caratteristiche delle potenze |
| ||
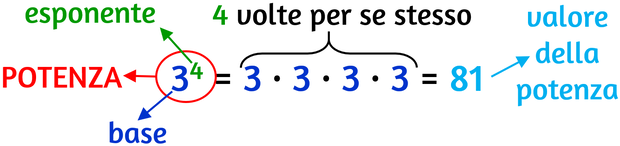
Una potenza è quell'operazione matematica che ha come valore il risultato di una moltiplicazione nella quale un numero, chiamato base, è moltiplicato per se stesso tante volte quanto indicato da un altro numero chiamato esponente.
|
Come si leggono le potenze
Con il simbolo # si indica qualunque numero
|
|
Prodotto di potenze che hanno la stessa base
Supponiamo di avere due potenze che devono essere moltiplicate tra loro e che hanno la stessa base, come ad esempio:
|
Da questa dimostrazione ecco la regola: il prodotto di due potenze che hanno la stessa base è una potenza che per base ha la stessa base e per esponente la somma degli esponenti.
La regola scritta in termini matematici è:
La regola scritta in termini matematici è:
|
Eccovi alcuni esempi, prima con solo numeri, poi con sole lettere, poi con potenze e basi diverse:
|
Quoziente di potenze che hanno la stessa base
Supponiamo di voler dividere tra di loro due potenze che hanno la stessa base, la divisione può essere scritta sotto forma di frazione, di modo da mettere in evidenza la quantità di fattori presenti al numeratore e presenti al denominatore, eccovi un esempio:
|
Da qui nasce la regola: il quoziente di due potenze che hanno la stessa base è una potenza che per base ha la stessa base e per esponente la differenza degli esponenti.
E la sua scrittura in formula matematica è:
E la sua scrittura in formula matematica è:
|
Ma se l'esponente della prima potenza è minore dell'esponente della seconda potenza?
Il risultato finale è una potenza con esponente negativo.
Il risultato finale è una potenza con esponente negativo.
|
Prodotto di potenze che hanno lo stesso esponente
Ora vediamo cosa succede quando vengono moltiplicate due o più potenze che hanno lo stesso esponente, nota bene nel terzo passaggio viene applicata la proprietà commutativa:
|
Da qui la regola: il prodotto di due potenze che hanno lo stesso esponente è una potenza che ha per base il prodotto delle basi e per esponente lo stesso esponente.
E ora riscriviamo la stessa regola in "matematichese":
E ora riscriviamo la stessa regola in "matematichese":
|
Quoziente di potenze con lo stesso esponente
E se anziché moltiplicare due o più potenze che hanno lo stesso esponente, le dividessimo? Vediamo insieme questo esempio:
|
Dal risultato ottenuto si arriva alla regola: il quoziente di due potenze che hanno lo stesso esponente, è una potenza che per base ha il quoziente tra le basi e per esponente lo stesso esponente.
Ed ecco la stessa regola scritta in forma sintetica:
Ed ecco la stessa regola scritta in forma sintetica:
|
Potenze di potenze
Ora vediamo cosa succede se la base di una potenza è a sua volta una potenza, in questo caso, come per le potenze semplici, la base è ripetuta tante volte quante volte è indicato dall'esponente, eccovi un esempio:
|
Una potenza di potenza è una potenza che ha per base la stessa base e per esponente il prodotto degli esponenti.
Eccovi invece la regola generale:
|
Potenze con esponente negativo
Cosa succede se dividiamo due potenze che hanno la stessa base ma l'esponente del dividendo è minore dell'esponente del divisore? Eccovi un esempio e osserviamo bene:
|
Come potete notare, i fattori al numeratore sono in quantità minore rispetto ai fattori presenti al denominatore, da cui ne deriva che, se applichiamo la regola vista per il quoziente di potenze che hanno la stessa base avremo l'esponente negativo, se invece la scriviamo sotto forma di frazione, al numeratore rimarrà uno e al denominatore la potenza derivante.
Eccovi la regola che ne deriva:
una potenza con esponente negativo è uguale ad una potenza con lo stesso esponente ma positivo e come base l'inverso della vecchia base.
Eccovi invece la regola generale scritta in "matematichese":
Eccovi la regola che ne deriva:
una potenza con esponente negativo è uguale ad una potenza con lo stesso esponente ma positivo e come base l'inverso della vecchia base.
Eccovi invece la regola generale scritta in "matematichese":
|
- se ad avere l'esponente negativo è un numero naturale
|
|
|
- se ad avere l'esponente negativo è una frazione
|
|
Potenze con base 1
Se la base di una potenza è 1, il suo valore sarà 1 qualunque sia l'esponente.
|
|
Un numero diviso se stesso dà come risultato 1 →
|
|
|
E se applichiamo la proprietà delle potenze aventi lo stesso esponente?
|
|
Potenze con esponente 1
Qualunque numero elevato 1 da come risultato la base.
|
Da qui la regola: qualunque potenza con esponente 1 ha come valore la base privata (tolto) l'esponente.
Potenze con esponente 0 (zero)
Una potenza con esponente zero non ha senso come scrittura a sé stante, ma la sua esistenza può essere giustificata da una divisione fatta tra potenze con uguale base ed uguale esponente.
Infatti per la proprietà sul quoziente di potenze aventi la stessa base, se esse avranno lo stesso esponente ne consegue che la differenza tra gli esponenti è uguale a zero, ed inoltre, poiché un numero diviso se stesso da come risultato 1, ecco dimostrata questa uguaglianza, un numero elevato zero da come risultato 1, escluso zero elevato zero che non ha significato.
Esempio:
Infatti per la proprietà sul quoziente di potenze aventi la stessa base, se esse avranno lo stesso esponente ne consegue che la differenza tra gli esponenti è uguale a zero, ed inoltre, poiché un numero diviso se stesso da come risultato 1, ecco dimostrata questa uguaglianza, un numero elevato zero da come risultato 1, escluso zero elevato zero che non ha significato.
Esempio:
|
Ecco il perché della regola: ogni potenza che ha come esponente 0 e come base qualunque numero escluso lo zero ha come valore 1.
|
Potenze con base ed esponente zero
Abbiamo visto che:
- se la base è zero il risultato è zero;
- se l'esponente è zero il risultato è 1.
|
non ha significato → nei libri delle medie
è indeterminato → dalle superiori in poi |
Dalle potenze di 10 al loro valore e viceversa
|
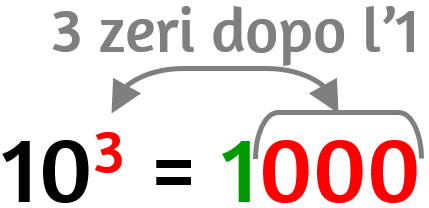
Quando una potenza ha come base 10 e come esponente un numero naturale ricorda:
|
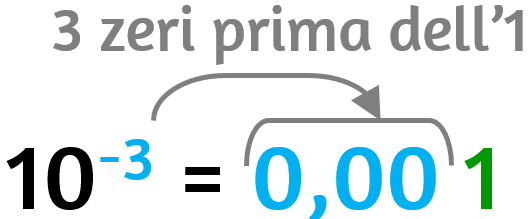
Quando una potenza ha come base 10 e come esponente un numero decimale ricorda:
|
Le espressioni con le potenze
Le espressioni aritmetiche o semplicemente espressioni, sono un susseguirsi di operazioni talvolta racchiuse all’interno di parentesi, che possono essere tonde ( ), quadre o quadrate [ ], oppure graffe { }.
Quali regole seguire quando si risolve un’espressione nella quale compaiono le potenze?
Quali regole seguire quando si risolve un’espressione nella quale compaiono le potenze?
- Si risolve ciò che sta dentro una parentesi tonda
- Potrò togliere la parentesi solo se al suo interno è rimasto solo un numero
- Posso applicare le proprietà delle potenze se queste sono moltiplicate o divise e se hanno o la stessa base o lo stesso esponente o sono potenze di potenze
- Se le potenze non hanno né stessa base né stesso esponente si risolvono singolarmente
- Se le potenze sono sommate o sottratte si risolvono singolarmente poi si sommano o si sottraggono
- Sottolinea sempre l’operazione o le operazioni che hanno la precedenza
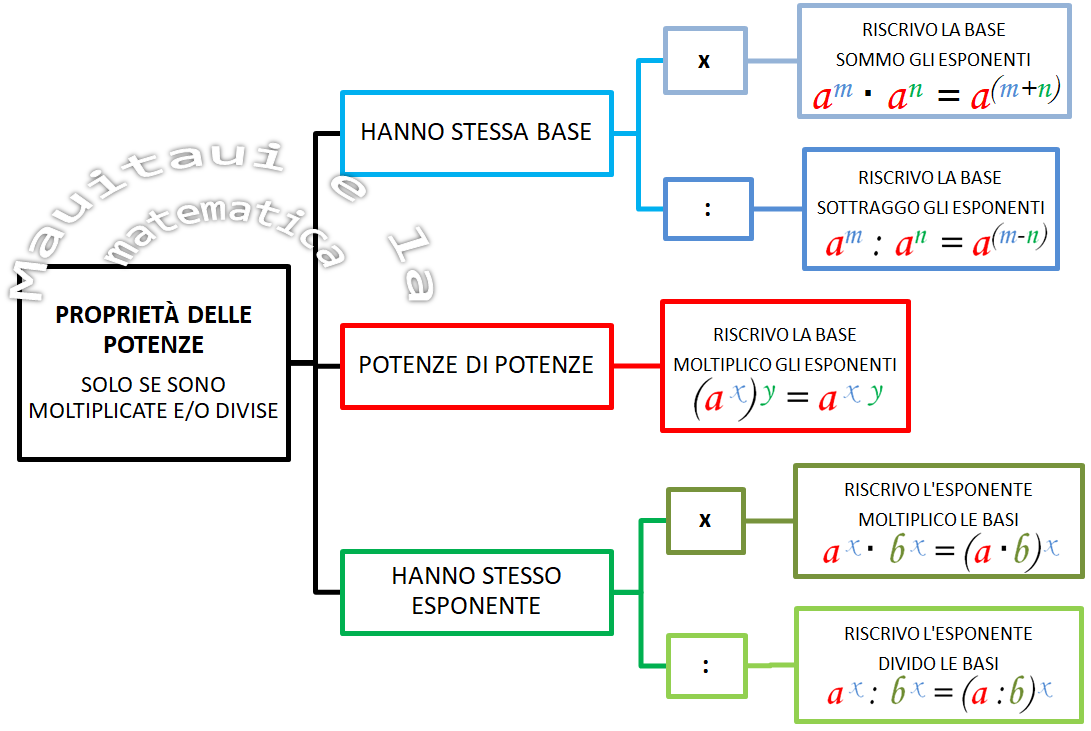
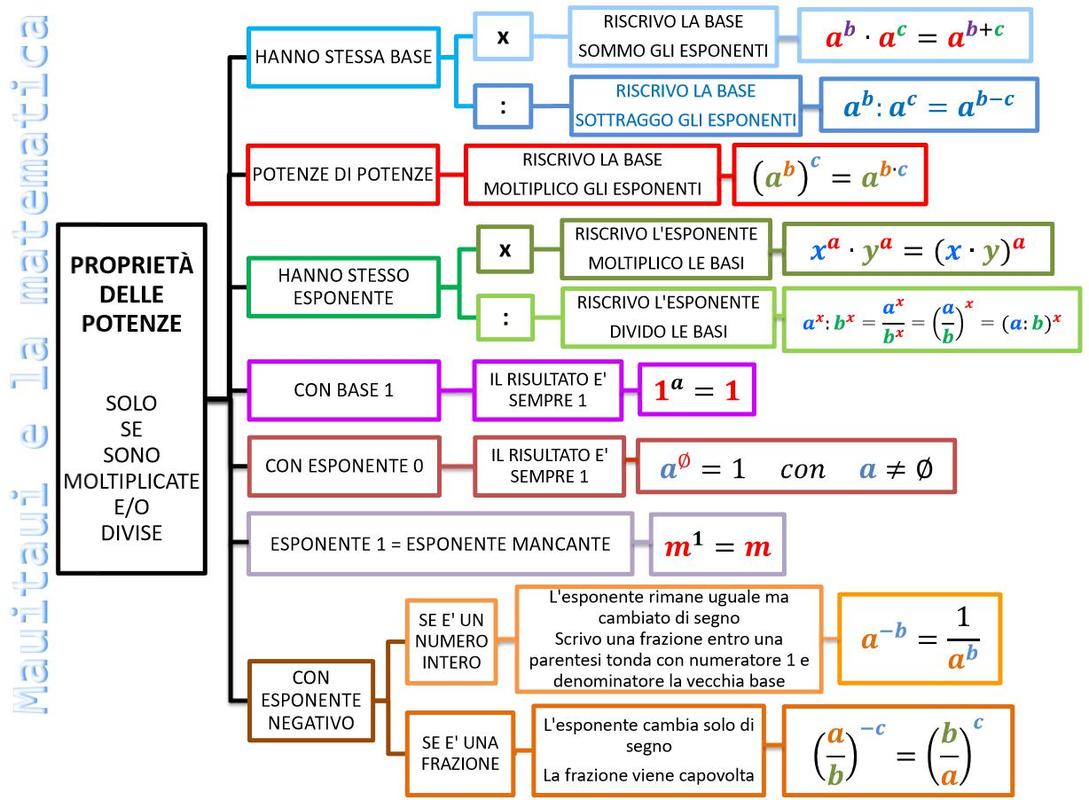
Schema riassuntivo
oppure a voi un altro schema, che trovate stampabile su materiali
Scrivere numeri grandi (≥ 10) o numeri piccoli (<1) in notazione scientifica
Leggere un numero molto grande o molto piccolo è talvolta difficile da fare, ed è per questo che per le misure sono state inventati i multipli e i sottomultipli.
Talvolta, però, i numeri sono veramente grandi o veramente molto vicini allo zero e neanche i multipli e i sottomultipli aiuterebbero a comprenderne l'ordine di grandezza appartenente alla misura.
In tal senso, le potenze di 10 aiutano a comprendere meglio le dimensioni del numero che stiamo scrivendo.
Sotto faccio due esempi su come scrivere un numero in notazione scientifica e su come viene riportato in una calcolatrice scientifica, sia nel caso di un numero molto grande che di un numero molto vicino allo zero.
Per poter fare ciò si scrive il numero in modo decimale ponendo come cifra delle unità la prima che compare diversa da zero partendo da sinistra, successivamente si scrive una potenza di 10 avente come esponente:
- il numero delle cifre totali meno la prima che funge da unità
Talvolta, però, i numeri sono veramente grandi o veramente molto vicini allo zero e neanche i multipli e i sottomultipli aiuterebbero a comprenderne l'ordine di grandezza appartenente alla misura.
In tal senso, le potenze di 10 aiutano a comprendere meglio le dimensioni del numero che stiamo scrivendo.
Sotto faccio due esempi su come scrivere un numero in notazione scientifica e su come viene riportato in una calcolatrice scientifica, sia nel caso di un numero molto grande che di un numero molto vicino allo zero.
Per poter fare ciò si scrive il numero in modo decimale ponendo come cifra delle unità la prima che compare diversa da zero partendo da sinistra, successivamente si scrive una potenza di 10 avente come esponente:
- il numero delle cifre totali meno la prima che funge da unità
Scrivere un numero in notazione scientifica vuol dire scrivere una moltiplicazione nella quale:
- il primo fattore è un numero intero o decimale maggiore o uguale a 1 e minore di 10;
- il secondo fattore è una potenza di 10 che può avere esponente:
- positivo (sottinteso) → se il numero originale è maggiore di 1;
- negativo → se il numero originale è compreso tra 0 e 1.
Scriviamo in notazione scientifica il numero 89 746
Come immettere il risultato in un foglio di calcolo: 8,9746*10^4 |
Scriviamo in notazione scientifica il numero 0,00935
Come immettere il risultato in un foglio di calcolo: 9,35*10^(-3) |
Dalla notazione scientifica all'ordine di grandezza
Definire l’ordine di grandezza di un numero è dare un’indicazione a quale potenza di 10 quella determinata quantità si avvicina di più.
Per conoscere l’ordine di grandezza di un numero dovremo:
Per conoscere l’ordine di grandezza di un numero dovremo:
- scrivere il numero in notazione scientifica
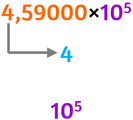
- controllare il primo fattore, se la parte intera del primo fattore è
|
1 2 3 4
|
5 6 7 8 9
|
|
ordine di grandezza uguale al
|
|
secondo fattore
con lo stesso esponente |
secondo fattore
con l'esponente aumentato di 1 |
Determiniamo l’ordine di grandezza del numero 459 000
|
Determiniamo l’ordine di grandezza del numero 8 320
|
Determiniamo l’ordine di grandezza del numero 0,00028
|
Determiniamo l’ordine di grandezza del numero 0,0000735
|
|
|
Contatore inserito il 11 agosto 2021
|