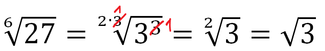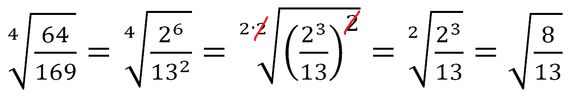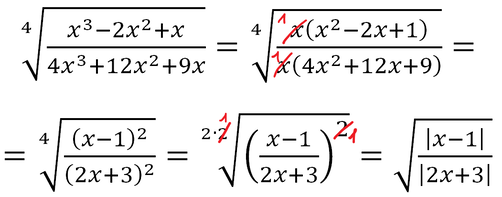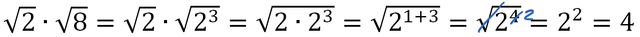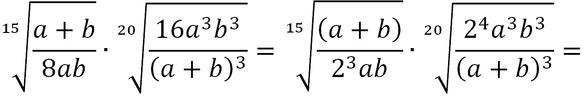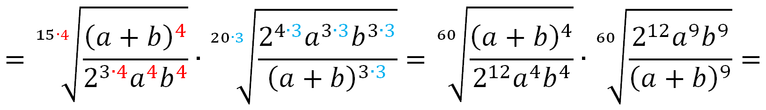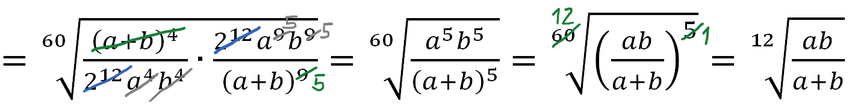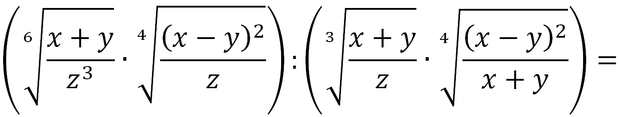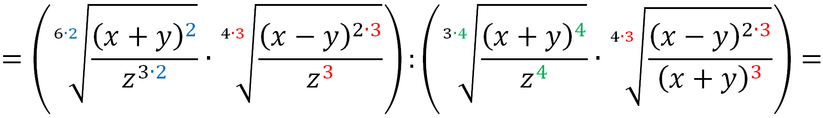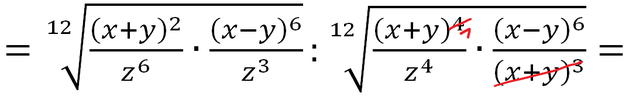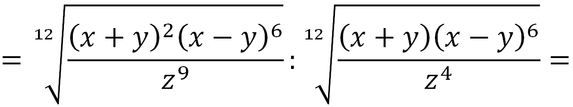ALTRI ESERCIZI CON I RADICALI
Semplificare un radicale
Semplificare un radicale vuol dire dividere per una quantità, la più grande possibile, sia l'indice della radice che gli esponenti di ciascun fattore dentro la radice.
Un radicale si dice irriducibile quando i due indici, della radice e del radicando, sono due numeri primi fra loro (cioè non hanno divisori in comune).
Importante: ricorda sempre di scrivere i numeri in fattori primi e che non è possibile semplificare una somma o una sottrazione.
Un radicale si dice irriducibile quando i due indici, della radice e del radicando, sono due numeri primi fra loro (cioè non hanno divisori in comune).
Importante: ricorda sempre di scrivere i numeri in fattori primi e che non è possibile semplificare una somma o una sottrazione.
Esempio 1
In questo esempio, ho:
a) scomposto il radicando in fattori primi;
b) semplificato gli indici per il MCD;
c) riscritto la radice quadrata omettendo l'indice della radice, che è
sottinteso.
a) scomposto il radicando in fattori primi;
b) semplificato gli indici per il MCD;
c) riscritto la radice quadrata omettendo l'indice della radice, che è
sottinteso.
Esempio 2
In questo esempio, ho:
a) scomposto numeratore e denominatore del radicando in fattori primi;
b) ricercato il MCD tra tutti gli indici (MCD tra 4, 6 e 2 è 2);
c) diviso ciascun indice per il MCD.
a) scomposto numeratore e denominatore del radicando in fattori primi;
b) ricercato il MCD tra tutti gli indici (MCD tra 4, 6 e 2 è 2);
c) diviso ciascun indice per il MCD.
Esempio 3
In questo esempio, ho:
- raccolto a fattor comune il numeratore e il denominatore (tutti i termini avevano sempre almeno una x);
- semplificato le due x messe in evidenza, ricordando che il risultato non potrà mai avere come soluzione x=0;
- scomposto il numeratore e il denominatore come quadrato di un binomio;
- poiché il quadrato di una qualunque espressione è sempre positiva o uguale a zero, nell'ultimo passaggio, non essendo più presente il quadrato, si usa come simbolo quello di "valore assoluto" (le due linee verticali che racchiudono ciascun binomio), che ci vuol dire che sia il numeratore che il denominatore dovranno essere sempre positivi.
Moltiplicazione e divisione tra radicali
- semplificare ciascun radicale;
- scomporre ciascun radicando;
- ridurre allo stesso indice ciascun radicale;
- scrivere ciascun radicando entro una stessa radice;
- eseguire le moltiplicazioni o le divisioni tra i radicandi.
Supponiamo di voler risolvere la seguente espressione
Visto che non è possibile semplificare nessun radicale, faremo:
- il mcm tra gli indici delle radici (mcm tra 6, 4 e 3 è 12)
- dividiamo ciascun indice per il mcm e moltiplichiamo sia gli indici che il radicando per il numero ottenuto
Riscrivo l'espressione con i nuovi esponenti e in un unica radice e semplifico numeratore con denominatore
Riscrivo l'espressione semplificata
Riscrivo il radicando del secondo radicale, trasformando la divisione in moltiplicazione ed invertendo numeratore e denominatore.
Semplifico e riscrivo quanto rimasto
Semplifico e riscrivo quanto rimasto