ALTRI SISTEMI DI NUMERAZIONE
Il sistema di numerazione binario
|
Il sistema di numerazione binario prende come riferimento due cifre, lo 0 e l'1.
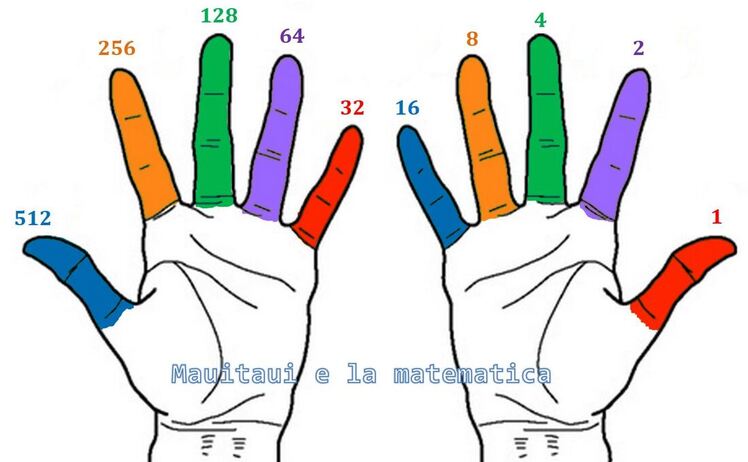
Le cifre che si trovano a destra hanno valore minore rispetto alle cifre che si trovano a sinistra, il valore di ciascuna cifra è uguale ad una potenza di 2. Ciò vuol dire che partendo da destra e andando verso sinistra il valore di ogni cifra è doppia della precedente. Il disegno sotto rappresenta le mani e il valore di ciascuna cifra.
Con due mani posso rappresentare tutti i numeri da 1 a 1023. La regola è: se il dito è sollevato quel valore c'è, se il dito è abbassato quel valore non c'è. |
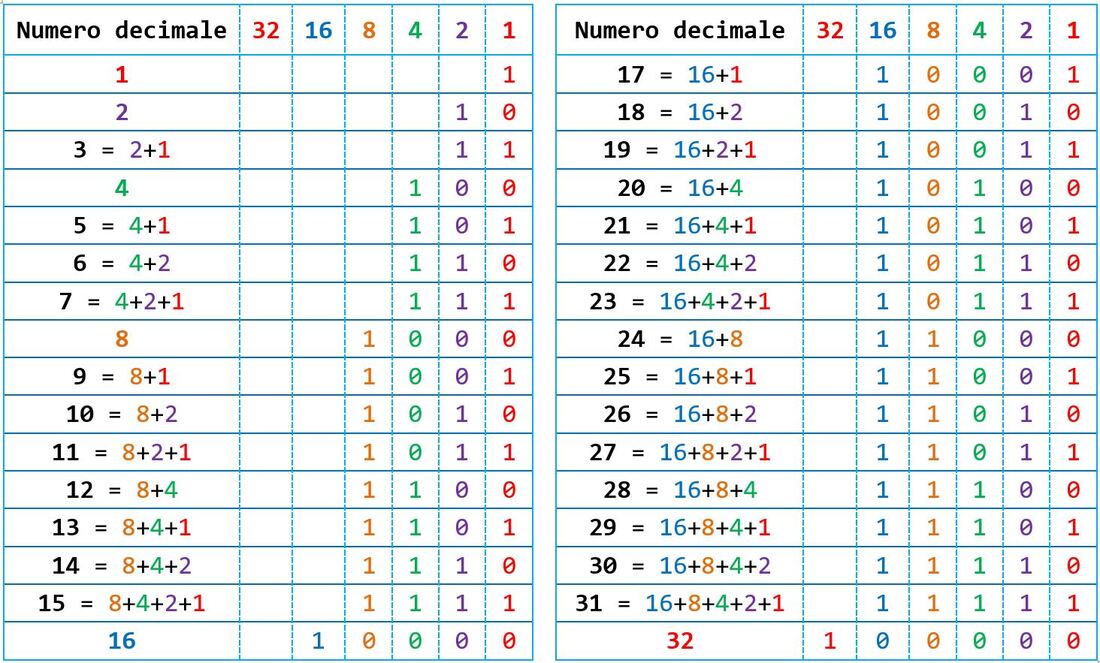
Confronto tra sistema binario e sistema decimale
Nella tabella seguente ho rappresentato i numeri da 1 a 32 del sistema decimale.
Dal decimale al binario e viceversa
La regola è:
posso usare solo i numeri 1, 2, 4, 8, 16, 32, 64, … per scomporre in addendi i numeri;
scompongo i numeri usando solo quelli sopra facendo una somma;
importante: i numeri sopra li posso usare solo una volta.
Esempio
Supponiamo di voler scrivere in binario il numero 73:
posso usare solo i numeri 1, 2, 4, 8, 16, 32, 64, … per scomporre in addendi i numeri;
scompongo i numeri usando solo quelli sopra facendo una somma;
importante: i numeri sopra li posso usare solo una volta.
Esempio
Supponiamo di voler scrivere in binario il numero 73:
- Tra i numeri sopra il più grande che sta nel 73 è il 64;
- Faccio la sottrazione 73 – 64 = 9
- Tra i numeri sopra il più grande che sta nel 9 è l’8;
- Faccio la sottrazione 9 – 8 = 1
- Tra i numeri sopra il più grande che sta nell’1 è l’1;
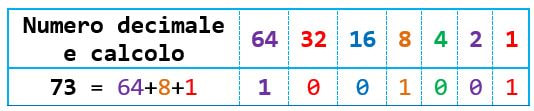
- Dunque posso scrivere che 73 = 64+8+1
- Partendo da sinistra scriverò 1 se quel numero c’è, 0 se il numero non c’è:
Possiamo affermare che il numero 73₁₀ si traduce in binario come 1001001₂.