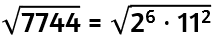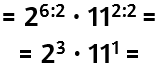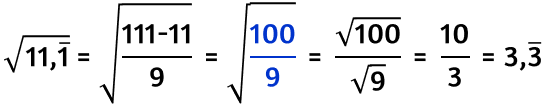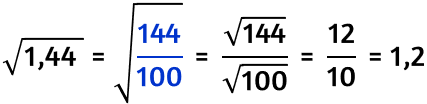LA RADICE QUADRATA
|
La radice quadrata è quell'operazione matematica che mi permette di ricavare quel numero che, moltiplicato per se stesso, ci dà come risultato il numero stesso.
Nel caso della radice quadrata, l'indice della radice 2 può essere omesso, in quanto non esiste indice naturale minore (se l'indice fosse 1 la presenza o meno della radice sarebbe invariato, l'indice 0 invece è dato non ammissibile).
|
Radice: qual è quel numero che moltiplicato per se stesso quante volte lo dice l’indice della radice mi dà il radicando?
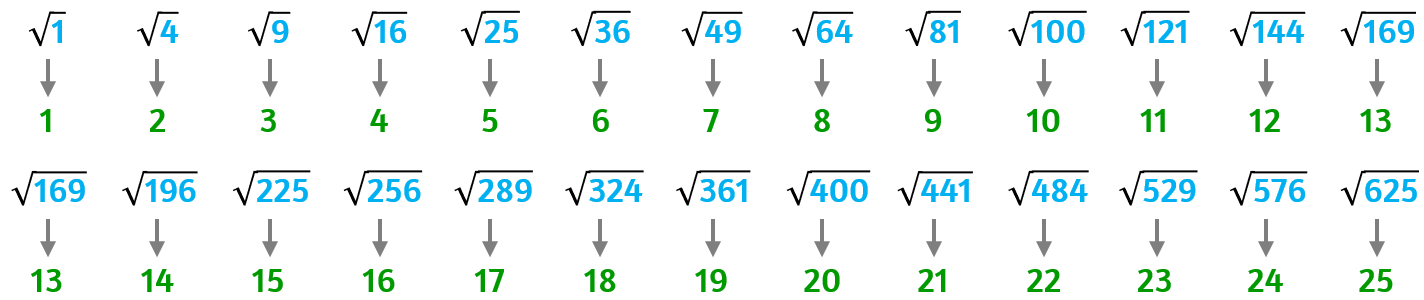
Si chiama quadrato perfetto quel numero la cui radice quadrata è un numero naturale.
La radice quadrata di un numero che non è un quadrato perfetto è un numero che dopo la virgola contiene un numero infinito di cifre decimali e prende il nome di numero irrazionale.
La radice quadrata di un numero che non è un quadrato perfetto è un numero che dopo la virgola contiene un numero infinito di cifre decimali e prende il nome di numero irrazionale.
Estrarre la radice quadrata di un quadrato perfetto
La radice quadrata di un quadrato perfetto è sempre un numero naturale (intero).
I quadrati perfetti finiscono sempre con 1, 4, 5, 6, 9 accompagnati o meno da un numero pari di zeri.
I quadrati perfetti finiscono sempre con 1, 4, 5, 6, 9 accompagnati o meno da un numero pari di zeri.
Come riconosco i quadrati perfetti?
Scomponendoli in fattori primi, gli esponenti sono sempre dei numeri pari.
|
144 = 2⁴ · 3²
|
144 potrebbe essere un quadrato perfetto perché finisce con 4;
144 è un quadrato perfetto perché nella sua scomposizione in fattori primi gli esponenti sono tutti pari; |
|
500 = 2² · 5³
|
500 potrebbe essere un quadrato perfetto perché finisce con due zeri e la cifra precedente è un 5;
500 non è un quadrato perfetto perché nella sua scomposizione in fattori primi gli esponenti NON sono tutti pari; |
|
123 = 3 · 41
|
123 non è un quadrato perfetto perché finisce con 3;
123 non è, infatti, un quadrato perfetto perché nella sua scomposizione in fattori primi gli esponenti NON sono tutti pari. |
Estrarre la radice quadrata di un numero che sappiamo essere un quadrato perfetto
|
= 8 · 11 = 88
|
La radice quadrata di numeri decimali derivanti da quadrati perfetti
La radice quadrata di un numero razionale (che può essere scritto come una frazione) può essere un numero razionale: la frazione generatrice semplificata ha per numeratore e denominatore due quadrati perfetti.
Se numeratore e denominatore sono due quadrati perfetti allora:
Algoritmo per il calcolo della radice quadrata
Per ricavare la radice quadrata di un numero che non è un quadrato perfetto, esiste un algoritmo (sequenza di operazioni che portano al risultato desiderato) che ci permette così di calcolarlo.
É importante ricordare che se voglio calcolare una radice di un numero che non è un quadrato perfetto, occorre avere un numero di cifre decimali in quantità doppia rispetto al numero di cifre che voglio avere nel risultato.
É importante ricordare che se voglio calcolare una radice di un numero che non è un quadrato perfetto, occorre avere un numero di cifre decimali in quantità doppia rispetto al numero di cifre che voglio avere nel risultato.
|
Cifre decimali nel risultato
1 2 3 4 |
Cifre decimali nel numero originale
2 4 6 8 |
Così se il numero che voglio ottenere deve avere due cifre decimali, andrò ad aggiungere tanti zeri quanti me ne occorrono per raggiungere le quattro cifre decimali che mi impone la regola, ma, in questo modo otterrò talvolta un numero troncato e non arrotondato, per avere la certezza di avere il risultato arrotondato dovrò conoscere la cifra successiva a quella da approssimare per difetto o per eccesso.
PRIMA DI ESTRARRE LA RADICE QUADRATA COSA DEVI SAPERE?
Separa le cifre del numero partendo dalla virgola, reale o immaginaria di fianco all'unità, di modo da formare gruppi di due cifre.
Il primo gruppo, della parte intera, può essere formato da una sola cifra.
Le cifre decimali sono sempre in gruppi di due, se dovessero essere dispari aggiungi uno zero alla loro destra.
Separa le cifre del numero partendo dalla virgola, reale o immaginaria di fianco all'unità, di modo da formare gruppi di due cifre.
Il primo gruppo, della parte intera, può essere formato da una sola cifra.
Le cifre decimali sono sempre in gruppi di due, se dovessero essere dispari aggiungi uno zero alla loro destra.
415,2 → 4.15,20 se voglio una cifra decimale e tronco il risultato ai decimi
→ 4.15,20.00 se voglio 2 cifre decimali e tronco il risultato ai centesimi
→ 4.15,20.00 se voglio 2 cifre decimali e tronco il risultato ai centesimi
385965 → 38.59.65 se non voglio nessuna cifra decimale e tronco il risultato all'unità
→ 38.59.65,00 se voglio una cifra decimale e tronco il risultato ai decimi
→ 38.59.65,00.00 se voglio due cifre decimali e tronco il risultato ai centesimi
→ 38.59.65,00 se voglio una cifra decimale e tronco il risultato ai decimi
→ 38.59.65,00.00 se voglio due cifre decimali e tronco il risultato ai centesimi
Nell'esempio che vi propongo sotto voglio estrarre la radice quadrata del numero 260 e voglio calcolare le prime due cifre decimali.
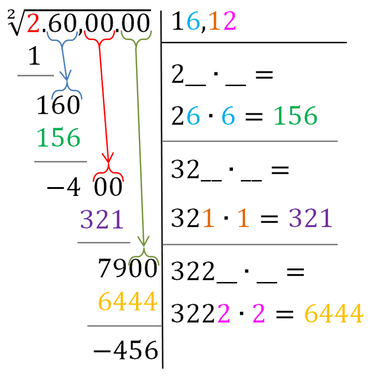
- mi chiedo, qual è quel numero ad una cifra che moltiplicato per se stesso mi da 2 o gli si avvicina senza superarlo? Questo numero è 1 e sotto il 2 scrivo il suo quadrato e, come per la divisione, eseguo una sottrazione.
- Abbasso il gruppo di cifre successive, 60, e ottengo 160.
- Al di sotto della stringa dedicata al risultato della radice scrivo il doppio del risultato fino a quel momento, un trattino basso, il segno di moltiplicazione ed un altro trattino basso. Al posto del trattino basso deve essere messo un numero ad una cifra, lo stesso per entrambi i trattini, tale che il risultato della moltiplicazione si avvicini senza superarlo il 160 ottenuto dal passaggio precedente.
- Anche stavolta scrivo sotto il 160 il risultato della moltiplicazione e calcolo la differenza tra entrambi.
- Abbasso il gruppo successivo di cifre.
- Sotto la moltiplicazione precedente metto una linea orizzontale per eseguire il prossimo passaggio.
- Scrivo il doppio del risultato fino a quel momento e aggiungo un trattino basso, il segno di moltiplicazione ed un altro trattino basso.
- Come al punto 3, ma cercando di non superare il 400.
- Procedo quante volte voglio dal punto 2) ricordando che il numero del quale devo fare il doppio non deve avere la virgola, anche se è presente nel risultato.
Il risultato 16,12 è un valore approssimato per difetto (o semplicemente troncato ai centesimi), se volessi arrotondare alla cifra dei centesimi avrei dovuto trovare anche la cifra dei centesimi.
LA RADICE CUBICA
Si chiama cubo perfetto quel numero la cui radice cubica è un numero naturale.
La radice cubica di un numero che non è un cubo perfetto, e la cui frazione generatrice del radicando non ha per numeratore e denominatore due cubi perfetti, è un numero che dopo la virgola contiene un numero infinito di cifre decimali che prende il nome di numero irrazionale.
La radice cubica di un numero che non è un cubo perfetto, e la cui frazione generatrice del radicando non ha per numeratore e denominatore due cubi perfetti, è un numero che dopo la virgola contiene un numero infinito di cifre decimali che prende il nome di numero irrazionale.
I cubi perfetti hanno come caratteristica quella di avere nella loro scomposizione in fattori primi solo potenze con esponente multiplo di 3.
|
125 = 5³
|
64 = 2⁶
|
216 = 2³ · 3³
|
Estrarre la radice cubica di cubi perfetti
Se hai di fronte a te un numero che sai essere un cubo perfetto e vuoi estrarre la sua radice cubica, o un numero già scomposto in fattori primi, ricorda che per estrarre la sua radice cubica dovrai dividere ciascun esponente per 3.
Eccoti i primi dieci cubi perfetti:
Contatore inserito il 25 febbraio 2021