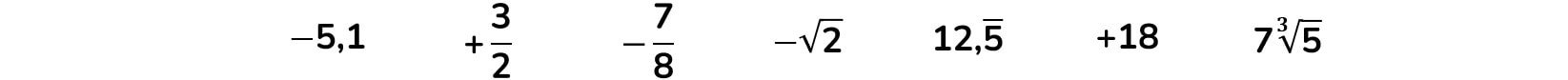I numeri relativi

CARATTERISTICHE DEI NUMERI RELATIVI

Si chiamano numeri relativi i numeri interi, razionali (che si possono esprimere come delle frazioni), irrazionali (radici), …, che sono anticipati o meno da un segno + o da un segno –.
I numeri preceduti dal segno "+" si dicono positivi (+8 +7 +14).
I numeri preceduti dal segno "-" si dicono negativi (-3 -15 -101).

Sono esempi di numeri relativi:

⚠ Se un numero non è anticipato da nessun segno è sottinteso il segno +

In una retta orientata orizzontale, posto 0 l'origine della retta:
- tutti i numeri alla sua destra sono positivi;
- tutti i numeri posti alla sinistra dello zero sono negativi.

Il valore assoluto

Quando togliamo il segno ad un numero relativo, vuol dire che stiamo considerando il suo valore assoluto o modulo.
Se voglio indicare il valore assoluto di un numero lo devo racchiudere entro due barre verticali |- 5| = 5 e si legge: il valore assoluto di "- 5" è "5".

Classificazione dei numeri relativi

Numeri concordi

Due numeri si dicono concordi quando sono entrambi positivi o entrambi negativi.
Due numeri concordi si trovano dalla stessa parte della retta orientata.

Numeri discordi

Due numeri si dicono discordi se uno è positivo e l’altro è negativo o viceversa.
Due numeri opposti si trovano da parti opposte della retta orientata.
-3 e 5 sono due numeri discordi.

Numeri opposti

Due numeri si dicono opposti se sono discordi e hanno lo stesso valore assoluto (cioè la parte numerica privata del segno è identica).
Sulla retta orientata si trovano da parti opposte
e rispetto allo zero hanno stessa distanza.

CONFRONTARE I NUMERI RELATIVI

In una retta orientata il numero che si trova più a destra è sempre maggiore di qualunque altro numero che si trova alla sua sinistra.

Stabilito chi dei due numeri è il maggiore e chi il minore, pensa al simbolo come ad un occhio aperto, l’occhio aperto guarda sempre il numero maggiore:

Se due numeri sono concordi positivi

Il più grande è il numero con il valore assoluto maggiore mentre il più piccolo è il numero con il valore assoluto minore.

Se due numeri sono concordi negativi

Il più grande è il numero con il valore assoluto minore mentre il più piccolo è il numero con il valore assoluto maggiore

Se due numeri sono discordi

Qualunque numero positivo è sempre più grande di qualunque numero negativo.

Lo zero e i numeri relativi

Lo zero è sempre maggiore di qualunque numero negativo e sempre minore di qualunque numero positivo.

Disporre i numeri in ordine crescente (dal minore al maggiore)

Prima i numeri negativi dal più grande in valore assoluto al più piccolo in valore assoluto.
Poi lo zero.
Infine i numeri positivi dal più piccolo al più grande.

Se i numeri sono decimali o misti o ci sono anche delle frazioni, prima di metterli in ordine usa uno dei due metodi sotto:

Metodo 1	Metodo 2
Riscrivi i numeri dati come frazioni come numeri con la virgola, puoi usare anche la tua calcolatrice.	Riscrivi tutti i numeri come frazioni e trasformarli in altre equivalenti aventi tutti lo stesso denominatore (meglio se è il mcm).

LE OPERAZIONI CON I NUMERI RELATIVI

Sommare (mettere insieme) numeri relativi

Tutte le differenze possono essere viste come delle somme algebriche in quanto per somma algebrica si intende «mettere insieme numeri relativi», siano essi positivi o negativi.

Mettere insieme due numeri positivi
Il risultato è dato dalla somma delle due quantità e il valore sarà sempre positivo.
(+7) + (+5) = +7 +5 = + 12 = 12

Mettere insieme due numeri negativi
Il risultato è dato dalla somma delle due quantità (la somma dei loro valori assoluti) ma il valore totale sarà negativo
(–7) + (–5) = –7 –5 = –(7 + 5) = –1

Mettere insieme un numero positivo e un numero negativo
Il maggiore in valore assoluto (numero privato del segno) è quello che dà il segno all’operazione, dopodiché si farà: quantità maggiore – quantità minore.
(+7) + (–5) = 7 – 5 = 2 → il risultato è positivo perché il maggiore in valore assoluto è +7
(–7) + (+5) = –(7 – 5) = –2 → il risultato è negativo perché il maggiore in valore assoluto è –7

Sottrarre (calcolare la differenza di) numeri relativi

Calcolare la differenza di due numeri relativi vuol dire eseguire la somma algebrica del primo numero (minuendo) e dell’opposto del secondo numero (sottraendo).

Togliere una quantità positiva ad un’altra positiva
Il risultato della differenza di due numeri positivi dipende dal valore assoluto di entrambi:

(+a) – (+b) = + a – b

se |+a| > |–b| → + a – b = positivo
+7 – (+5) = +7 – 5 = + 2

se |+a| < |–b| → + a – b = negativo
+5 – (+7) = +5 – 7 = – 2

Togliere una quantità negativa ad un’altra negativa
Il risultato della differenza di due numeri negativi dipende dal valore assoluto di entrambi:

(–a) – (–b) = – a + b

se |–a| > |+b| → – a + b = negativo
–7 – (–5) = – 7 + 5 = – 2

se |–a| < |+b| → – a + b = positivo
– 5 – (–7) = – 5 + 7 = + 2

Togliere una quantità negativa ad un’altra positiva
Il risultato di questa differenza è uguale ad un numero positivo il cui valore assoluto è uguale alla somma dei valori assoluti delle due quantità:

(+a) – (+b) = + a + b = + (a + b)

+7 – (+5) = +7 + 5 = + (7 + 5) = + 12

Togliere una quantità positiva ad un’altra negativa
Il risultato di questa differenza è uguale ad un numero negativo il cui valore assoluto è uguale alla somma dei valori assoluti delle due quantità:

Segno + davanti ad una parentesi
→ lascia inalterato il segno di ciò che sta nella parentesi.
Segno – davanti ad una parentesi
→ cambia il segno di ciò che sta nella parentesi

Le somme algebriche

Supponiamo di avere di fronte una somma algebrica, cioè una serie di numeri anticipati da un segno positivo o negativo e nella quale non compaiono né segni di moltiplicazione né segni di divisione:

6 - 5 - 8 + 4 - 14 + 7 - 8 + 5 =

sottolineare o evidenziare tutti i numeri negativi:

= 6 – 5 – 8 + 4 – 14 + 7 – 8 + 5 =

Nella somma algebrica sono presenti numeri opposti? Se sì eliminali a vicenda:

= 6 – 5 – 8 + 4 – 14 + 7 – 8 + 5 =
= 6 – 8 + 4 – 14 + 7 – 8 =

mettere all'interno di una parentesi tutti i numeri concordi positivi;
chiudere la parentesi, mettere il segno - e aprirne un'altra nella quale mettere tutti i numeri concordi negativi, ma legati tra loro dal segno + (stiamo mettendo INSIEME i numeri negativi);
chiudere la parentesi e mettere il segno di =

= (6 + 4 + 7) – (8 + 14 + 8) =

4. sommare i termini di ciascuna parentesi

= 17 – 30 = – (30 –17) = –13

Per fare la somma algebrica vi propongo un esempio, tanto coi soldi siamo tutti bravi! Supponiamo di voler acquistare un qualcosa (quantità negativa perché i soldi li spendo) e ho a disposizione una certa somma di denaro (quantità positiva).
Ciò che voglio acquistare:

ha un prezzo inferiore di quanto possiedo? → il risultato finale sarà positivo, +;
ha un prezzo superiore di quanto possiedo? → il risultato finale sarà negativo, –;

Ora sottrai la quantità maggiore alla quantità minore senza considerare il loro segno.

IMPORTANTE
Se anziché avere a che fare con i numeri naturali (interi) avessimo numeri razionali (esprimibili tramite delle frazioni) e/o irrazionali (non esprimibili tramite frazioni, come le radici quadrate) le regole sopra esposte sarebbero identiche.

Il prodotto di numeri relativi

Prodotto dei segni (amico = + nemico = –)

L’amico del mio amico è mio amico
L’amico è mio nemico è mio nemico
Il nemico del mio amico è mio nemico
Il nemico del mio nemico è mio amico

+ · + = +
+ · – = –
– · + = –
– · – = +

Innanzitutto ricordiamo che il prodotto è il risultato di una moltiplicazione.
Quando abbiamo a che fare con il prodotto di due o più numeri relativi occorre operare nel modo seguente:

Moltiplicare i segni
Moltiplicare i numeri
Il risultato avrà il segno ottenuto al punto 1. e il prodotto ottenuto nel punto 2.

Moltiplicare due o più numeri positivi

Il prodotto di due o più numeri positivi è sempre positivo:

(+2)(+3)(+4)(+5) = + 2 · 3 · 4 · 5 = + 120

(+7)(+5) = + 7 · 5 = + 35

Moltiplicare due o più numeri negativi

Il prodotto di due o più numeri negativi dipende dalla quantità dei fattori:

se la quantità dei fattori è pari
il prodotto è positivo
(–2)(–3)(–4)(–5) = + 2 · 3 · 4 · 5 = + 120

se la quantità dei fattori è dispari
il prodotto è negativo
(–2)(–3)(–2)(–5)(–4) = – 2 · 3 · 2 · 5 · 4 = – 240

Moltiplicare due o più numeri relativi misti (positivi e negativi)

Il prodotto di due o più numeri relativi dipende dalla quantità dei fattori negativi:

se la quantità dei fattori negativi è pari
il prodotto è positivo
(+2)(–3)(–4)(+5) = + 2 · 3 · 4 · 5 = + 120

se la quantità dei fattori negativi è dispari
il prodotto è negativo
(+2)(+3)(–2)(+5) = – 2 · 3 · 2 · 5 · 4 = – 60

Se i numeri relativi sono numeri razionali visti sottoforma di frazioni, si opera nel seguente modo:

Moltiplicare prima i segni
Riscrivere le frazioni una di fianco all'altra
Semplificare, se è possibile, qualunque numeratore con qualunque denominatore
Moltiplicare tra di loro i numeratori rimasti e poi moltiplicare tra di loro i denominatori rimasti
Il risultato avrà come segno finale il risultato ottenuto nel punto 1. e come numero quanto ottenuto nel punto 4.

Quoziente di numeri relativi

Innanzitutto ricordiamo che il quoziente è il risultato di una divisione. Essendo la divisione l'operazione inversa della moltiplicazione, ne consegue che le regole sono esattamente le stesse per quanto riguarda il quoziente dei segni.

+ : + = +
+ : – = –
– : + = –
– : – = +

Quando abbiamo a che fare con la divisione di due o più numeri relativi, per quanto riguarda il segno, ci si comporta come per il prodotto di numeri relativi:

dividi o moltiplica i segni
dividi le quantità numeriche
il risultato avrà il segno ottenuto al punto 1. e la quantità ottenuta nel punto 2.

Dividere due numeri positivi
Il quoziente di due numeri positivi è sempre positivo: (+14) : (+7) = + 14 : 7 = + 2

Dividere due numeri negativi
Il prodotto di due numeri negativi è sempre positivo: (–12) : (–3) = + 12 : 3 = + 4

Dividere due numeri discordi
Il quoziente di due numeri discordi (uno positivo e l’altro negativo o viceversa)
è sempre negativo:
(+12) : (–3) = (–12) : (+3) = – 12 : 3 = – 4

Le potenze di numeri relativi (con esponente naturale)

Per quanto riguarda le potenze di numeri relativi occorre ricordare che le regole viste in aritmetica sono le stesse in algebra.

Qui di seguito vedremo cosa succede quando l'esponente è un numero pari, un numero dispari o un numero negativo.

IMPORTANTE: se la base di una potenza è un numero negativo occorre SEMPRE scriverla tra parentesi, in caso contrario la potenza avrà come base solo il numero e non il suo segno:

(–6)² ≠ –6²
infatti
(–6)² = (–6)(–6) = +36 mentre –6² = – 6 · 6 = –36

Nello schema che vi presento sotto si deduce che, una potenza ha come valore un numero negativo SOLO e SOLO SE la base è negativa e l’esponente è dispari:

Base	Esponente	Valore della potenza	Esempio
positiva	pari o dispari	positivo	(+3)⁵ = (+3) (+3) (+3) (+3) (+3) = +3⁵ = +243
negativa	pari	positivo	(–2)⁴ = (–2) (–2) (–2) (–2) = +2⁴ = +16
negativa	dispari	negativo	(–5)³ = (–5) (–5) (–5) = –5³ = –125

Potenze con esponente negativo

Il valore di una potenza con esponente negativo è uguale ad una potenza che avrà come base l’inverso della vecchia base e come esponente il valore assoluto del vecchio esponente:

Se la base è un numero intero dovrai scrivere una frazione che ha:

come numeratore il numero 1;
come denominatore la vecchia base;
come esponente il valore assoluto del vecchio esponente negativo.

Se la base è una frazione dovrai scrivere una frazione che ha:

come numeratore il vecchio denominatore;
come denominatore il vecchio numeratore;
come esponente il valore assoluto del vecchio esponente negativo.

Espressioni con i numeri relativi

Quando si svolgono le espressioni, le regole viste per l'aritmetica valgono anche per l'algebra.
Ricorda di rispettare le precedenze, nel caso specifico ricorda:

se la relazione è di addizione e sottrazione ricordati di mettere sempre insieme i positivi e poi insieme i negativi;
se la relazione è di moltiplicazione e divisione, esegui le operazioni esattamente nell'ordine in cui si presentano, moltiplica prima i segni e poi esegui le operazioni tra i numeri.

Ripassa bene le operazioni con le frazioni, come trovare la frazione generatrice di un numero decimale.

Eccovi qui di seguito alcuni esempi di espressioni, da molto semplici a molto articolate, spero possano esservi di aiuto.

16 – (51) – 4 + (+3) + (–19) – (–51) – (+9) + 11 =