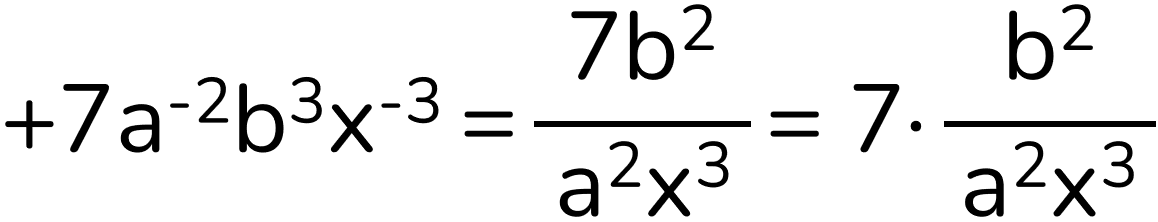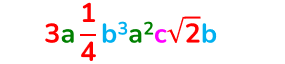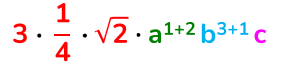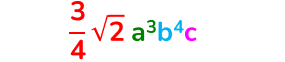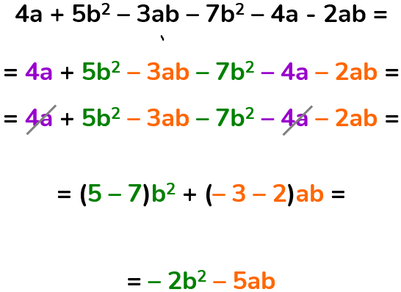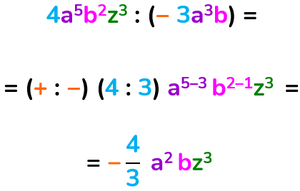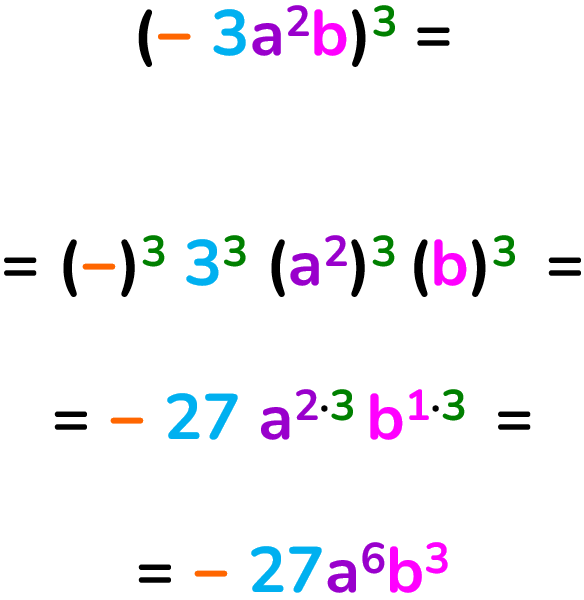I MONOMI

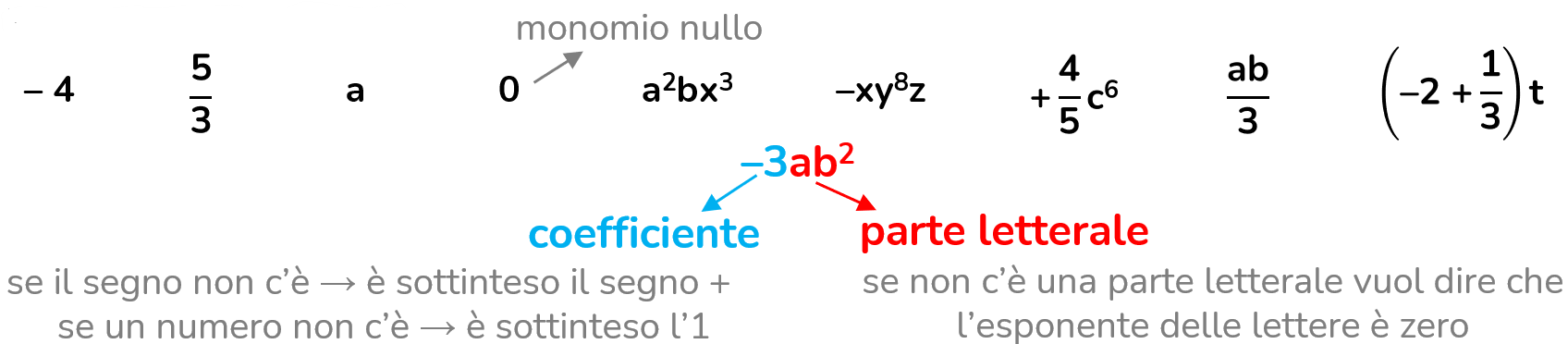
Si chiama monomio quell'espressione letterale, composta da:

• un numero (naturale, relativo, razionale e/o irrazionale),
• una lettera o un insieme di lettere (con esponente naturale = con esponente intero e positivo)
• o da numeri e lettere, il cui legame tra loro sottinteso è di moltiplicazione.

–3ab² = –3·a·b²

Sono esempi di monomi: ​

Un monomio si dice intero se la parte letterale ha esponente positivo e si trova al numeratore di una qualsiasi frazione (l'esempio sopra è quello di un monomio intero).

Un monomio che ha come coefficiente un numero razionale (cioè una frazione) non è un monomio frazionario se gli esponenti di tutte le lettere sono numeri interi e positivi.

Un monomio si dice frazionario se almeno una lettera della parte letterale al numeratore ha esponente negativo o si trova al denominatore con esponente positivo. Questo tipo particolare di monomio costituisce una frazione algebrica.

---

Ridurre un monomio alla forma normale

Un monomio è ridotto alla forma normale quando:

• la parte numerica è composta da un numero razionale, irrazionale o un insieme di questi;
• la parte letterale è formata da potenze aventi tutte come basi lettere tra loro diverse.

Il monomio non è scritto nella forma normale perché la parte numerica è formata da due numeri razionali e quella letterale è formata da più potenze aventi talvolta la stessa base.

Scrivi prima tutti i numeri e metti assieme le stesse le stesse basi della parte letterale (in ordine alfabetico) applicando le proprietà delle potenze. ​

Risolvi sia la parte numerica (coefficiente) che la parte letterale.

---

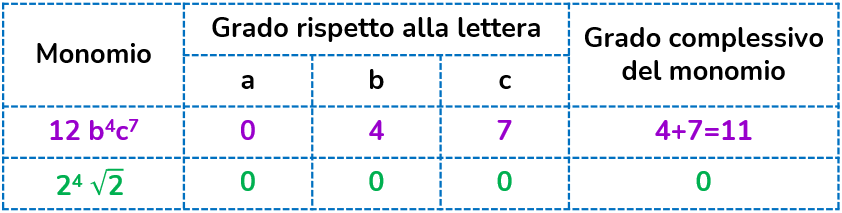
Grado di un monomio

Grado di un monomio o grado complessivo di un monomio → la somma degli esponenti di tutte le lettere che formano la parte letterale: 8x³y ha come grado complessivo 3+1 = 4
Grado di un monomio rispetto ad una lettera → l’esponente posseduto dalla lettera considerata.​

I monomi che sono formati da solo la parte numerica, il coefficiente, vengono chiamati termini noti. Il grado di questo monomio particolare è sempre zero. ​

---

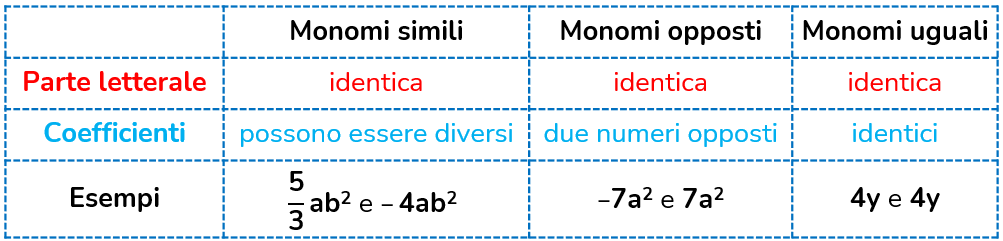
Monomi simili, opposti e uguali

I monomi simili, opposti e uguali hanno la caratteristica di avere tutti la stessa parte letterale.

---

Il valore di un'espressione letterale

Per trovare il valore di un'espressione letterale dobbiamo avere il valore di ciascuna delle incognite (lettere) che compaiono.

Trova il valore della seguente espressione letterale:

4a²xy³ + 5ax – 15 a³y
con a = 1, x = –2, y = –1

• sostituiamo alla lettera a il valore di 1;
• sostituiamo alla lettera x il valore di (–2);
• sostituiamo alla lettera y il valore di (–1);
• mettiamo in evidenza il segno di moltiplicazione tra i numeri e le lettere all'interno dello stesso monomio;
• successivamente risolvi l'espressione aritmetica che ne risulta. 

= 4 · 1² · (–2) · (–1)³ + 5 · 1 · (–2) – 15 · 1³ · (–1) =
= 4 · 1 · (–2) · (–1) + 5 · 1 ·(–2) – 15 · 1 · (–1) =
= 8 – 10 + 15 = 23 – 10 = 13

---

LE OPERAZIONI CON I MONOMI

Somma e differenza tra monomi

Due o più monomi possono essere sommati e/o sottratti tra loro solo se sono simili (hanno stessa parte letterale, sia nel tipo di lettere che nell'esponente abbinato alla lettera).

Si procede in questo modo:

• per prima cosa mettiamo in evidenza tutti i monomi simili
• controlla se ci sono monomi opposti e eliminali a vicenda
• metti in una parentesi i coefficienti appartenenti alla stessa «famiglia» di monomi simili e fuori dalla famiglia indica la parte letterale del monomio di riferimento
• risolvi le parentesi tonde così come hai visto precedentemente

monomio 1	monomio 2	monomio 1 + monomio 2	monomio 1 – monomio 2
4a²y³	–3xy³	4a²y³ + (–3xy³)	4a²y³ – (–3xy³)
4a²y³	–3xy³	4a²y³ – 3xy³	4a²y³ + 3xy³

• Se i monomi che sommi e/o sottrai sono tra loro tutti simili → ottieni come risultato un unico monomio
• Se i monomi che sommi e/o sottrai non sono simili → ottieni come risultato un insieme di monomi ​diversi (in quantità uguale o minore alle tipologie di monomi presenti) che si chiama polinomio

---

Moltiplicare due o più monomi

Posso moltiplicare tra loro sia monomi simili che monomi diversi.
Il risultato del prodotto di due o più monomi tra loro è sempre un monomio.
Moltiplicare due o più monomi equivale a scrivere il monomio in forma normale, in quanto tra numeri e lettere è sottinteso già il segno di moltiplicazione. 

Quando si moltiplicano tra loro due o più monomi occorre:	4a · (− 5b²) · (− 3a³b) =
moltiplica i segni; moltiplica i numeri (valori assoluti dei coefficienti); infine moltiplica la parte letterale usando le proprietà delle potenze (se hanno la stessa base, riscrivi la stessa base e somma gli esponenti).	= (−)(−) · 4 · 5 · 3 · a¹ · a³ · b² · b¹ = ​= + 60 a⁴ b³

Se moltiplichiamo	Otteniamo come risultato	Esempio
due monomi simili	il prodotto dei coefficienti e il quadrato della parte letterale	6a³ · 2a³ = = 6·2 (a³)² = ​= 12 a⁶
due monomi uguali	il quadrato di tutto il monomio	(–5x) · (–5x) = = (–5x)² = ​= +25x²
due monomi opposti	il quadrato di tutto il monomio ma negativo	(7y²) · (–7y²) = = –(7y²)² = ​= –49y⁴

---

Quoziente tra monomi

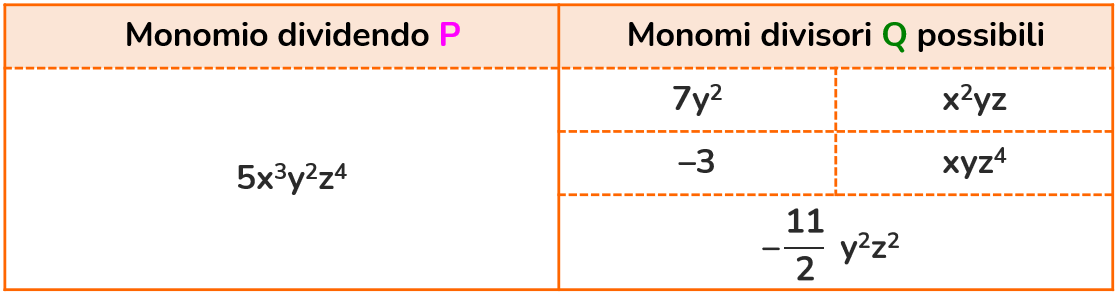
Un monomio P è divisibile per un altro Q quando il quoziente P : Q è uguale a un altro monomio.
Un monomio Q è divisore di un altro monomio P quando tutte le sue lettere sono contenute nel monomio Q ma con un esponente pari o minore. 

Si procede in questo modo:

1. dividi i segni;
2. dividi i numeri (se non sono divisibili scrivi il risultato come frazione e riducila ai minimi termini);
3. infine dividi la parte letterale applicando le proprietà delle potenze (se hanno la stessa base, riscrivi la base e sottrai gli esponenti).

Se dividiamo tra loro	Il risultato è	Esempio
due monomi simili	un numero dato dal quoziente dei due coefficienti	6a³ : 2a³ = 3
due monomi uguali	è uguale a 1	(–5x) : (–5x) = 1
due monomi opposti	è uguale a –1	(7y²) : (–7y²) = –1

Non tutte le divisioni tra monomi danno come risultato un monomio:
l’operazione di divisione non è interna all’insieme dei monomi. ​

---

Potenza di un monomio

Il risultato di della potenza di un monomio si ottiene elevando a quella potenza ciascun termine del monomio (sia il coefficiente che la parte letterale). ​

Si procede in questo modo:

1. Se l’esponente è pari: il risultato è sempre positivo.
   Se l’esponente è dispari: il risultato ha lo stesso segno della base.
2. Trova il valore della potenza del numero (moltiplica per se stesso il numero quante volte lo indica l’esponente della potenza del monomio);
3. Fai la potenza di ciascuna lettera che compone la parte letterale del monomio (la potenza di una potenza è uguale ad una potenza che avrà come base la stessa base e avrà come esponente il prodotto degli esponenti).

La potenza con esponente zero di un monomio è uguale a 1 se e solo se il valore di ciascuna delle lettere presenti nella parte letterale sia imposta come diversa da zero.

---

MCD tra monomi

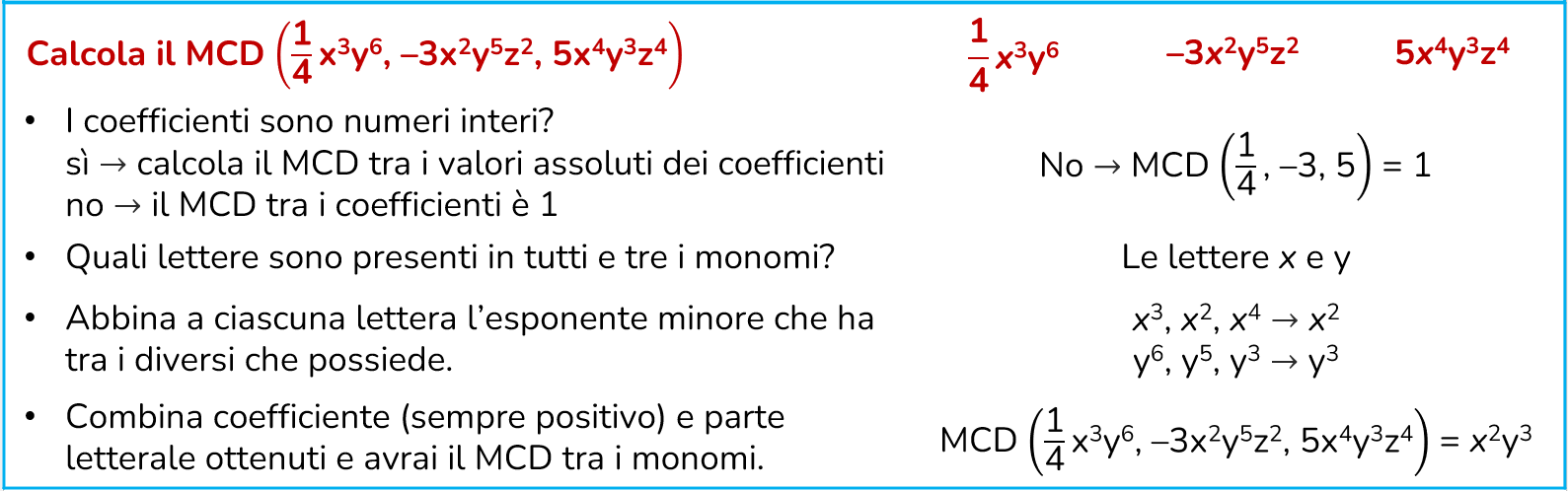
Calcolare il MCD vuol dire trovare quei monomi, di grado massimo, capaci di dividere tutti i monomi presenti. Tra i MCD in generale si avrà come:

• coefficiente   →   1 se almeno un monomio non è intero;
                          →   il MCD di tutti i valori assoluti dei coefficienti se tutti i coefficienti sono interi.
• parte letterale → prodotto delle lettere comuni a tutti, prese una sola volta, con l’esponente più piccolo presente.

---

mcm tra monomi

Calcolare il mcm vuol dire trovare quei monomi, di grado minimo, che sono contemporaneamente multipli di tutti i monomi presenti. Tra i mcm, in generale, si avrà come:

• coefficiente   → 1 se almeno un monomio non è intero;
                         → il mcm di tutti i valori assoluti dei coefficienti se tutti i coefficienti sono interi.
• parte letterale → basi comuni e non comuni a tutti, prese una sola volta, con l’esponente più grande presente.

contatore inserito il 15 luglio 2021