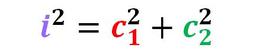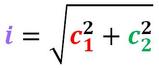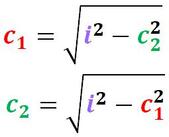Cos'è il Teorema di Pitagora? |
| ||
Il teorema di Pitagora è il celeberrimo teorema matematico che permette di trovare la misura di uno dei lati di un triangolo rettangolo conoscendo gli altri due lati.
Si chiama triangolo rettangolo quel triangolo che ha un angolo retto.
Si chiamano cateti i lati che formano l'angolo retto.
Si chiama ipotenusa il lato opposto all'angolo retto.
Ricorda: l'ipotenusa è sempre il lato più lungo.
Si chiamano cateti i lati che formano l'angolo retto.
Si chiama ipotenusa il lato opposto all'angolo retto.
Ricorda: l'ipotenusa è sempre il lato più lungo.
Eccovi due modi classici di rappresentare un triangolo rettangolo.
Nel primo disegno il triangolo rettangolo è stato inscritto in una semicirconferenza.
Nel secondo disegno sono stati disegnati i due cateti come due lati tra loro perpendicolari.
Nel primo disegno il triangolo rettangolo è stato inscritto in una semicirconferenza.
Nel secondo disegno sono stati disegnati i due cateti come due lati tra loro perpendicolari.
Sposta i cursori negli sliders oppure sposta il pallino nella semicirconferenza.
Il teorema di Pitagora dice che:
in un triangolo rettangolo, il quadrato costruito sull'ipotenusa ha la stessa area della somma dei quadrati costruiti sui due cateti.
in un triangolo rettangolo, il quadrato costruito sull'ipotenusa ha la stessa area della somma dei quadrati costruiti sui due cateti.
|
I numeri dentro i quadrati indicano
la misura della loro area. Cambia le misure dei due cateti. |
I numeri dentro i quadrati indicano la misura della loro area.
Cambia la misura dell'ipotenusa oppure muovi il pallino sulla semicirconferenza per cambiare la misura dei cateti |
Una prima dimostrazione grafica del teorema di Pitagora
Nell'animazione sotto ho costruito dei quadrati sui lati del triangolo.
Successivamente ho disegnato 8 triangoli, identici a quello a sinistra e li ho disposti a formare due quadrati con il lato congruente alla somma delle lunghezze dei due cateti.
Nel quadrato centrale i triangoli lasciano 2 spazi, ciascuno dei quali ha il lato congruente ai cateti del triangolo rettangolo, nel quadrato a destra, invece, la disposizione dei triangoli mette in evidenza un quadrato avente come lato l'ipotenusa.
I due quadrati disegnati hanno la stessa area e sono così composti:
Successivamente ho disegnato 8 triangoli, identici a quello a sinistra e li ho disposti a formare due quadrati con il lato congruente alla somma delle lunghezze dei due cateti.
Nel quadrato centrale i triangoli lasciano 2 spazi, ciascuno dei quali ha il lato congruente ai cateti del triangolo rettangolo, nel quadrato a destra, invece, la disposizione dei triangoli mette in evidenza un quadrato avente come lato l'ipotenusa.
I due quadrati disegnati hanno la stessa area e sono così composti:
|
Quadrato centrale
4 triangoli rettangoli 2 quadrati |
Quadrato a destra
4 triangoli rettangoli 1 quadrato |
Avendo la stessa area ne consegue che se ad ognuno tolgo aree equivalenti, a ciascun quadrato rimane la stessa quantità di superficie, anche se disposta in modo diverso, da questo ne consegue che, se elimino i 4 triangoli rettangoli sia dal quadrato centrale che da quello a destra, l'area del quadrato che ha come lato l'ipotenusa ha la stessa estensione della somma dei due quadrati che hanno come lato i due cateti.
Una seconda dimostrazione del teorema di Pitagora
|
L'immagine a destra vuole essere un'altra dimostrazione del teorema di Pitagora.
A colore uguale corrisponde figura geometrica uguale. Sposta il pallino "muovi", osserva come viene divisa l'immagine quando il cursore sta esattamente a metà o occupa altre posizioni.
|
|
Le formule del teorema di Pitagora
Grazie al teorema di Pitagora possiamo conoscere:
Ricorda
Quando devo trovare la misura dell'ipotenusa o dei due cateti dovrò fare le operazioni con il seguente ordine:
Quando devo trovare la misura dell'ipotenusa o dei due cateti dovrò fare le operazioni con il seguente ordine:
- Riscrivo la formula che mi occorre per trovare ciò che mi manca
- Sostituisco alle lettere i valori numerici
- Faccio il quadrato dei numeri
- Eseguo la somma o la differenza
- Estraggo la radice quadrata
Contatore inserito il 31 marzo 2021