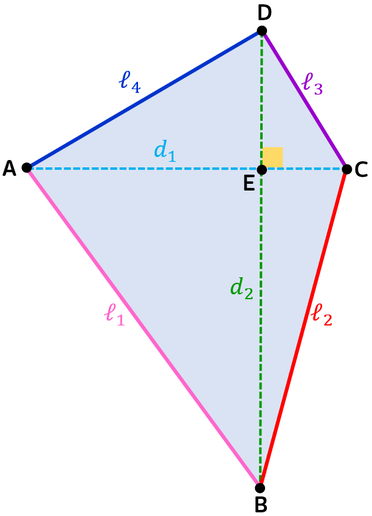
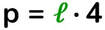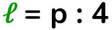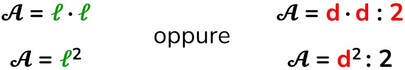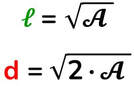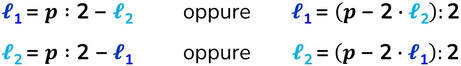PERIMETRO E AREA DEI QUADRILATERI
- Perimetro → parola che deriva dal greco perì (=intorno) + métron (=misura).
In geometria sta a indicare la misura del contorno di un poligono → si ottiene sommando la lunghezza di tutti i lati
Indicherò il perimetro con la lettera minuscola p (e non con 2p come fanno alcuni testi), questo perché il perimetro è uno e il suo semiperimetro, che spesso compare in altre formule, secondo me deve essere indicato come p:2). - Area → è la misura dell'estensione della sua superficie → si può ottenere con formule dirette o con somma o differenza di aree di altre figure piane.
In una figura piana la superficie è quella parte di piano che ha come confine il perimetro della figura che sto considerando.
Indicherò l'area con la lettera A maiuscola, così come fanno la maggior parte dei testi.
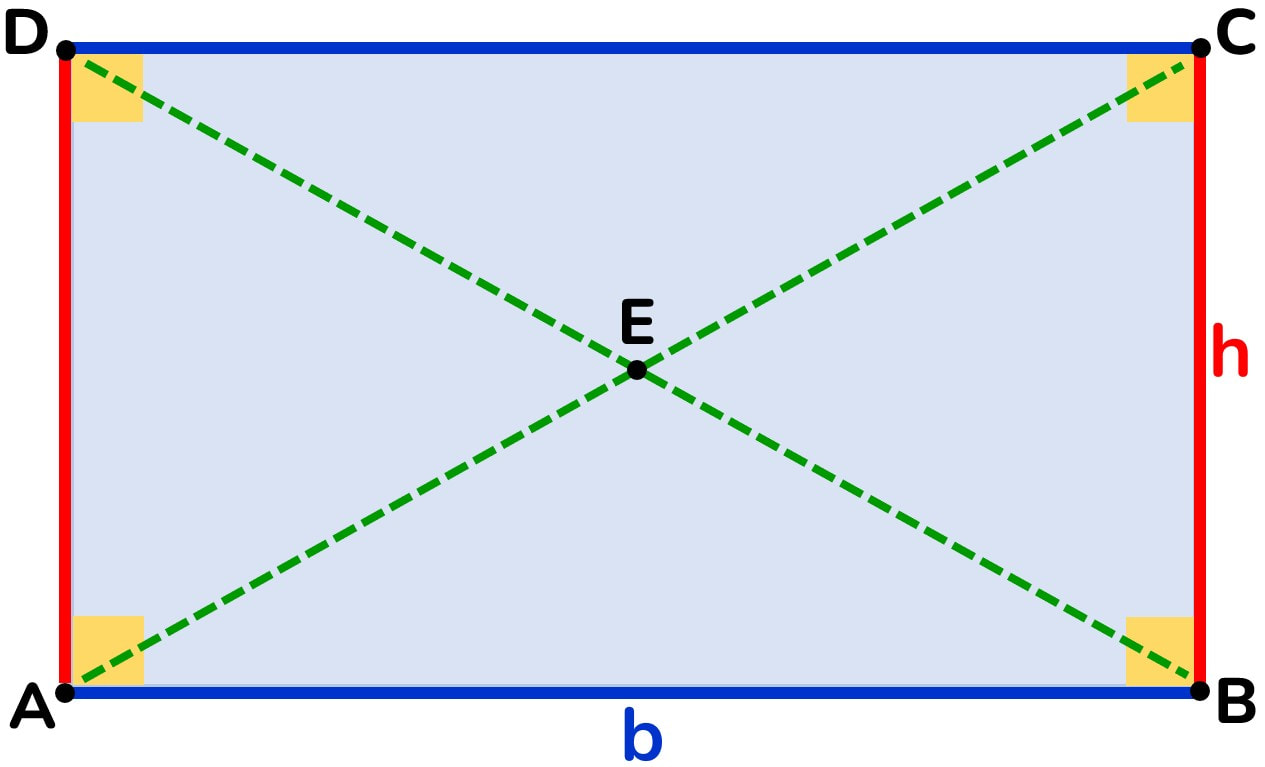
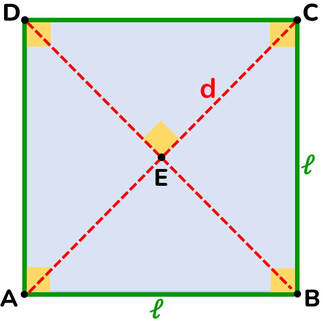
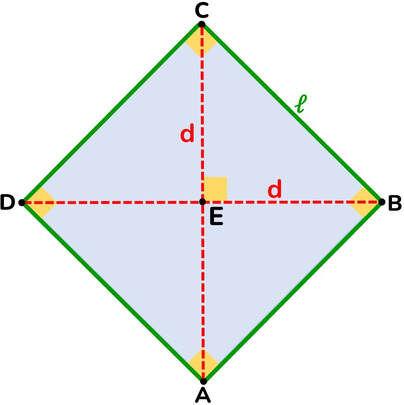
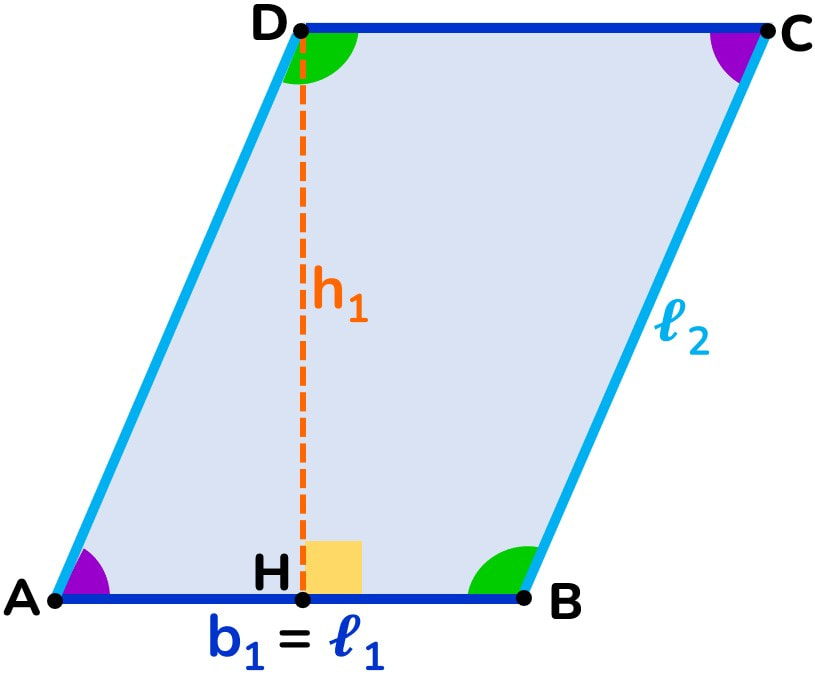
OGNI QUADRILATERO:
- ha 4 lati
- ha 4 angoli
- la somma degli angoli interni è 360°
IL RETTANGOLO
|
IN TUTTI I RETTANGOLI:
|
⚠
Le dimensioni nel rettangolo sono i suoi lati: la base e l'altezza. |
Video spiegazioni
Problema 1:
In un rettangolo le sue dimensioni sono una i 3/4 dell'altra e la misura della dimensione maggiore è di 16 cm. Calcola il perimetro e l'area del rettangolo.
Problema 2:
In un rettangolo la base è i 7/4 dell'altezza, mentre il suo perimetro misura 66 cm. Calcola l'area del rettangolo.
Problema 3:
In un rettangolo la differenza tra le misure della base e dell'altezza è di 6 cm, mentre il loro rapporto è di 10 a 7. Calcola il perimetro e l'area del rettangolo.
Problema 4:
In un rettangolo le sue dimensioni sono una 1 4/5 dell'altra e la sua area ha un'estensione di 180 cm². Calcola il perimetro del rettangolo.
In un rettangolo le sue dimensioni sono una i 3/4 dell'altra e la misura della dimensione maggiore è di 16 cm. Calcola il perimetro e l'area del rettangolo.
Problema 2:
In un rettangolo la base è i 7/4 dell'altezza, mentre il suo perimetro misura 66 cm. Calcola l'area del rettangolo.
Problema 3:
In un rettangolo la differenza tra le misure della base e dell'altezza è di 6 cm, mentre il loro rapporto è di 10 a 7. Calcola il perimetro e l'area del rettangolo.
Problema 4:
In un rettangolo le sue dimensioni sono una 1 4/5 dell'altra e la sua area ha un'estensione di 180 cm². Calcola il perimetro del rettangolo.
IL QUADRATO
|
IN TUTTI I QUADRATI:
|
|
⚠
|
Un quadrato è un rettangolo con i lati congruenti.
Un quadrato è un rombo con le diagonali congruenti. |
|
|
IL PARALLELOGRAMMA
IN TUTTI I PARALLELOGRAMMI:
- i lati opposti sono congruenti → AB ≅ CD e BC ≅ AD
- i lati opposti sono paralleli → AB || CD e BC || AD
- gli angoli opposti sono congruenti → α ≅ γ e β ≅ δ
- gli angoli adiacenti sono supplementari → α + β = β + γ = γ + δ = δ + α = 180°
- Ogni diagonale incontra l’altra nel proprio punto medio.
|
Il fatto che il parallelogramma abbia due coppie di lati paralleli, fa conseguire che ciascun lato può essere considerato come base.
|
IL ROMBO
IN OGNO ROMBO:
- tutti i lati sono congruenti → AB ≅ BC ≅ CD ≅ AD
- i lati opposti sono paralleli → AB || CD e AD || BC
- le diagonali sono perpendicolari → AC ⊥ BD
- gli angoli opposti sono congruenti
- le altezze relative a ciascun lato sono congruenti
(perché sono congruenti anche i lati) - ogni diagonale incontra l’altra nel proprio punto medio.
|
|
IL TRAPEZIO
IN OGNI TRAPEZIO:
- c'è una coppia di lati paralleli che prendono il nome di basi
- i lati non paralleli prendono il nome di lati obliqui
- gli angoli adiacenti a ciascun lato obliquo supplementari
α + δ = β + γ = 180°
|
|
|
TRAPEZIO ISOSCELE
OLTRE ALLE CARATTERISTICHE VALIDE PER OGNI TRAPEZIO, QUELLO ISOSCELE HA:
- i lati obliqui congruenti → AD ≅ BC
- le diagonali congruenti → AC ≅ BD
- gli angoli adiacenti a ciascuna base congruenti → α + δ = β + γ = 180°
|
|
|
TRAPEZIO RETTANGOLO
Nel trapezio rettangolo il lato obliquo minore è perpendicolare alle due basi e diventa così altezza del trapezio.
|
|
|
L'AQUILONE
OGNI AQUILONE HA:
- le diagonali perpendicolari
- due coppie di lati consecutivi congruenti
- una diagonale che taglia a metà l'altra
- una diagonale è bisettrice degli angoli disuguali (compresi tra i lati congruenti)
- una coppia di angoli congruenti (compresi tra i lati disuguali)
|
|
QUADRILATERI CON LE DIAGONALI PERPENDICOLARI
Non hanno nessuna caratteristica particolare esclusa quella di avere le diagonali perpendicolari.
|
|
|
|
Ultima modifica il 24 aprile 2021
|