I NUMERI NELLA NUMERAZIONE DECIMALE

Caratteristiche della numerazione decimale

Il nostro sistema di numerazione è il sistema decimale[1] posizionale:

• decimale perché i simboli usati sono dieci (0 1 2 3 4 5 6 7 8 9) e il salto da una cifra ad un'altra posta al suo fianco va di dieci in dieci,
• posizionale perché il valore di ciascuna cifra dipende dalla posizione che occupa.

[1] Il sistema decimale, originario dell’India, fu portato in Europa dagli Arabi (per questo motivo chiamiamo i numeri che utilizziamo numeri arabi).

Per poter leggere con facilità e per comprendere la quantità di un numero composto da tante cifre dovremo innanzitutto dividerlo in classi, mettendo un puntino o una virgoletta in alto separando gruppi di 3 cifre.

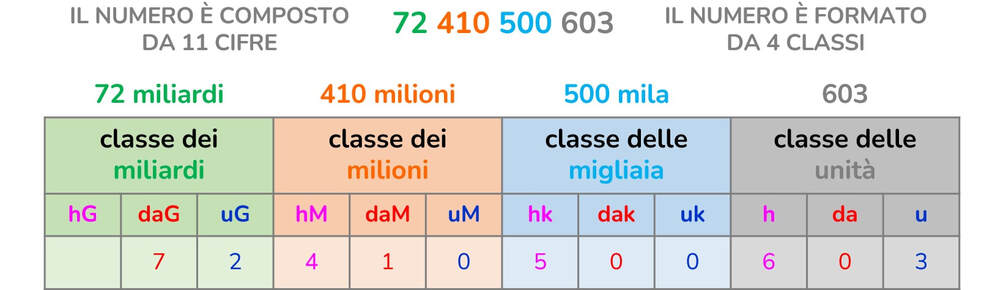
Supponiamo di avere il numero: 5091458.
Come si legge questo numero e che valore hanno le sue cifre? 72410500603

Per prima cosa dividiamo in gruppi di tre le cifre, partendo da destra: 72 410 500 603

Ho diviso il numero in gruppi di tre cifre, partendo da destra, mi compaiono 4 gruppi, che in matematichese prendono il nome di classi. Per cui, essendo il numero intero:

• il primo gruppo partendo da destra è la CLASSE DELLE UNITÀ
• il secondo gruppo partendo da destra è la CLASSE DELLE MIGLIAIA
• il terzo gruppo partendo da destra è la CLASSE DEI MILIONI
• l'ultimo gruppo, il quarto, composto da 2 cifre, è quello della CLASSE DEI MILIARDI 

Ogni classe che si trova più a destra di ogni altra classe deve essere formata sempre da tre cifre.
L'ultimo gruppo partendo da destra, o il primo partendo da sinistra (la classe con il valore maggiore), può essere composto da una, due o tre cifre.

Numeri interi e numeri decimali

I numeri naturali sono quelli che si usano per contare: sono sempre interi (la parte decimale è sempre uguale a zero) e sono positivi.
I numeri naturali sono infiniti → ℕ = {0; 1; 2; 3; 4; 5; 6; …}

I numeri decimali sono quei numeri con la virgola, hanno una parte intera (uguale o maggiore a zero) e una parte decimale, a destra della virgola. 

​Man mano che cresciamo e cominciamo a misurare lunghezze, altezze, quantità di materia... vediamo che la misura non è poi così precisa se la indichiamo con un numero intero, e così si rende necessario utilizzare numeri che mostrano non solo le quantità intere ma anche i pezzettini che non raggiungono l'intero, come 

• l’altezza del mio zio preferito (un metro e settantotto centimetri = 1,78 m),
• il peso dei panini che devo portare in gita per tutta la classe (due chilogrammi e trecento grammi = 2,300 kg = 2,3 kg)

I numeri interi possono essere scritti come numeri decimali mettendo una virgola e degli zeri

814 = 814,0 = 814,00 = 814,000 = 814,000…

---

Gli zeri utili e gli zeri inutili

Si parla di zero utile quando la sua presenza è fondamentale per stabilire il valore di ciascuna delle cifre → se togliamo uno zero utile il valore del numero, e conseguentemente delle sue cifre cambia. 

• 903 → lo zero è utile perché se lo elimino il valore della cifra 9 cambia
• 096 → lo zero è inutile perché se lo elimino non cambia il valore di nessuna cifra
• 4,5701 → lo zero è utile perché se lo elimino il valore della cifra 1 cambia
• 37,980 → lo zero è inutile perché se lo elimino non cambia il valore di nessuna cifra

---

Precedente e successivo di un numero

Si chiama precedente quel numero che si ottiene togliendo 1 al numero che sto considerando: il precedente di 86 è 86-1 cioè 85.
Si chiama successivo quel numero che si ottiene aggiungendo 1 al numero che sto considerando: il successivo di 297 è 297+1 cioè 298.

---

Confrontare due numeri interi o decimali

Se la parte intera di due numeri è composta da una quantità di cifre diverse, il numero maggiore ha una quantità di cifre maggiore:

Se la parte intera è uguale confronta i decimi: 
​a cifra dei decimi maggiore corrisponde numero maggiore
4,32 < 4,2

Se anche la cifra dei decimi è uguale confronta la cifra dei centesimi: 
​a cifra dei centesimi maggiore corrisponde numero maggiore
​0,42 < 0,411

Puoi confrontare due numeri decimali con la stessa parte intera operando in questo modo:

• aggiungi tanti zeri quanti sono necessari perché la quantità di cifre decimali nei due numeri sia uguale
• ora puoi confrontare solo la parte decimale trattandola come se fosse intera

---

Ordinare i numeri naturali in ordine crescente

Ordine crescente → dal più piccolo al più grande

Ordinare i numeri in ordine crescente vuol dire disporli dal più piccolo al più grande. Metteremo per primi i numeri con un numero minore di cifre e per ultimi i numeri con la quantità maggiore di cifre. 
Ricordiamo che a parità di cifre, il minore sarà quelle che avrà come prima cifra il numero minore, se la prima cifra considerata è uguale allora si procederà ad analizzare la seconda cifra a sinistra, la minore indicherà il numero minore, a parità di valore si procede analogamente alle cifre immediatamente in terza posizione e via discorrendo. Facciamo un esempio che possa aiutarci a capire meglio. 

0 è minore di 1 che è minore di 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9

Mettiamo in ordine crescente i numeri: 489 – 95 - 405 – 63 – 8 - 6

• Ricerca i numeri composti da una cifra:
  - mettili in ordine dal più piccolo al più grande
• Ricerca i numeri composti da due cifre:
  - è minore il numero con la cifra delle decine minore
  - se hanno la stessa decina sarà minore quello con la cifra delle unità minore
• Ricerca i numeri composti da tre cifre:
  - è minore il numero con la cifra delle centinaia minore
  - se la cifra delle centinaia è la stessa nei due numeri, allora sarà minore quello con la cifra delle decine minore
  - se anche la cifra delle decine è uguale, allora sarà minore quello con la cifra delle unità minore
• Metti insieme i numeri dei tre gruppi nello stesso ordine

Ordinare i numeri interi in ordine decrescente

Vuol dire ordinare i numeri dal più grande al più piccolo.
Metterò per primi i numeri che hanno un numero maggiore di cifre e per ultimi i numeri che ne hanno un numero minore. 
​A parità di numero di cifre il numero che avrà la cifra più a sinistra maggiore indicherà il valore maggiore, a parità di valore si analizzeranno le cifre che si trovano più a destra.

Mettiamo in ordine crescente i numeri: 819 – 6 – 53 - 810 – 63 – 7

• Ricerca i numeri composti da più cifre (in questo caso tre):
  - è maggiore il numero con la cifra delle centinaia maggiore
  - se la cifra delle centinaia è la stessa nei due numeri, allora sarà maggiore quello con la cifra delle 
  ​   decine maggiore
  - se anche la cifra delle decine è uguale, allora sarà maggiore quello con la cifra delle unità maggiore
• Ricerca i numeri composti da due cifre:
  - è maggiore il numero con la cifra delle decine maggiore
  - se hanno la stessa decina sarà maggiore quello con la cifra delle unità maggiore
• Ricerca i numeri composti da una cifra:
  - mettili in ordine dal più grande al più piccolo
• Metti insieme i numeri dei tre gruppi nello stesso ordine

---

Ordinare i numeri con la virgola

Per poter confrontare i numeri con la virgola occorre:

1. confronta prima la parte intera, se la parte intera è diversa sarà maggiore il numero con la parte intera maggiore e sarà minore quello con la parte intera minore;
2. se la parte intera è uguale dovrai ricercare tra i numeri quello che ha il più grande numero di cifre decimali (sono le cifre dopo la virgola)
3. aggiungere tanti zeri ai numeri decimali, di modo da portarli tutti ad una stessa quantità di cifre decimali
4. confrontare i numeri come se non avessero la virgola, ricordando che a parità di parte intera si confronta la parte decimale, a parte decimale maggiore, composta dalla stessa quantità di cifre decimali, corrisponde numero maggiore e viceversa.

USA PURE LA TABELLA SOPRA

 Mettiamo in ordine decrescente (dal più piccolo al più grande) i seguenti numeri:
13,8 - 2,987 - 13,65 - 8,9 - 8,456 - 6,06 - 2,99  - 6,6 

1. per prima cosa riscriviamo i numeri con una stessa quantità di cifre decimali, aggiungendo degli zeri per colmare il vuoto (sono presenti al massimo tre cifre decimali, dunque ciascun numero dovrà avere tre cifre decimali)
   13,800 - 2,987 - 13,650 - 8,900 - 8,456 - 6,060 - 2,990 - 6,600
2. ora possiamo disporre i numeri in ordine decrescente
   13,800 - 13,650 - 8,900 - 8,456 - 6,600 - 6,060 - 2,990 - 2,987 
3. togliamo gli zeri inutili
   13,8 - 13,65 - 8,9 - 8,456 - 6,6 - 6,06 - 2,99 - 2,987 

Mettiamo in ordine crescente i numeri: 4,89 – 4,95 – 4,05 – 4,3 – 4,008 - 4
Qual è il massimo di cifre decimali possedute dal numero? 3 cifre
Aggiungi a ciascun numero tanti zeri alla parte decimale quanti sono necessari ad avere la stessa quantità di cifre decimali in tutti i numeri

4,890 – 4,950 – 4,050 – 4,300 – 4,008 – 4,000

Confronta prima la parte intera e disponi i numeri in ordine crescente le parti intere.
Se la parte intera è uguale confronta la parte decimale, considerando in ordine:

• le cifre dei decimi → 4,050 – 4,008 – 4,000 - 4,300 – 4,890 – 4,950
• le cifre dei centesimi → 4,008 – 4,000 - 4,050 – 4,300 – 4,890 – 4,950
• le cifre dei millesimi → 4,000 - 4,008 – 4,050 – 4,300 – 4,890 – 4,950​

4,000 - 4,008 - 4,050 - 4,300 - 4,890 – 4,950 ​

Elimina gli zeri inutili e riscrivi i numeri

4 - 4,008 - 4,05 - 4,3 - 4,89 – 4,95 ​

Il valore delle cifre e la scrittura polinomiale

Il valore di ciascuna cifra dipende non solo dal tipo di cifra ma anche dalla posizione che occupa. Vediamo un esempio:

In generale la cifra che sta immediatamente a destra di un altra è sempre più piccola di dieci volte, mentre la cifra che sta immediatamente a sinistra di un altra è più grande di 10 volte.

Ricorda:
1 unità = 10 decimi = 100 centesimi = 1000 millesimi
1 decina = 10 unità = 100 decimi = 1000 centesimi = …
1 centinaia = 10 decine = 100 unità = 1000 decimi = …
1 migliaia = 10 centinaia = 100 decine = 1000 unità = …