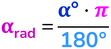Goniometria

LA GONIOMETRIA

La misura degli angoli in geometria

Gli angoli vengono misurati in gradi e altre volte in radianti.

Misura in radianti
È la lunghezza dell'arco sotteso un angolo al centro di una circonferenza di raggio uguale a 1.

Angoli in radianti e in gradi
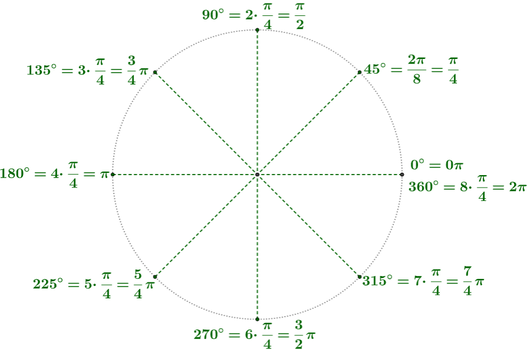
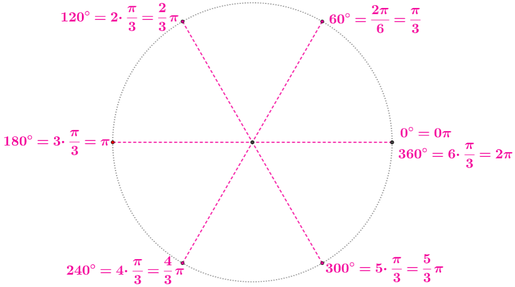
Lunghezza della circonferenza = 2π · r = 2π · 1 = 2π = 360°
Semicirconferenza = 2π : 2 = π = 360° : 2 = 180°
Un sesto di semicirconferenza = π : 6 = π/6 = 180° : 6 = 30°
Un quarto di semicirconferenza = π : 4 = π/4 = 180° : 4 = 45°
Un terzo di semicirconferenza = π : 3 = π/3 = 180° : 3 = 60°
Metà semicirconferenza = π : 2 = π/2 = 180° : 2 = 90°
...

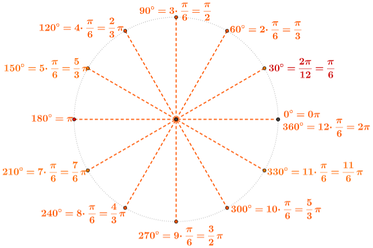
Se dividiamo la circonferenza in 12 parti uguali otteniamo dei settori circolari che sottendono angoli al centro di 30° e archi di π/6.

Se dividiamo la circonferenza in 8 parti uguali otteniamo dei settori circolari che sottendono angoli al centro di 45° e archi di π/4.

Se dividiamo la circonferenza in 6 parti uguali otteniamo dei settori circolari che sottendono angoli al centro di 60° e archi di π/3.

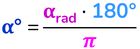
Dalla misura in gradi a quella in radianti e viceversa

Impostiamo la proporzione:
lunghezza arco : lunghezza circonferenza = angolo al centro : angolo giro
αrad : 2π = α° : 360°

Dai gradi ai radianti

1° = π/180
2° = π/90
3° = π/60
4° = π/45
5° = π/36
6° = π/30
7° = 7π/180
8° = 2π/45
9° = π/20
10° = π/18

11° = 11π/180
12° = π/15
...
15° = π/12
...
18° = π/10
...
20° = π/9
...
24° = 2 · 12° = 2π/15

27° = 3 · 9° = 3π/20
...
30° = π/6
...
36° = π/5
...
45° = π/4
...
60° = π/3
90° = π/2

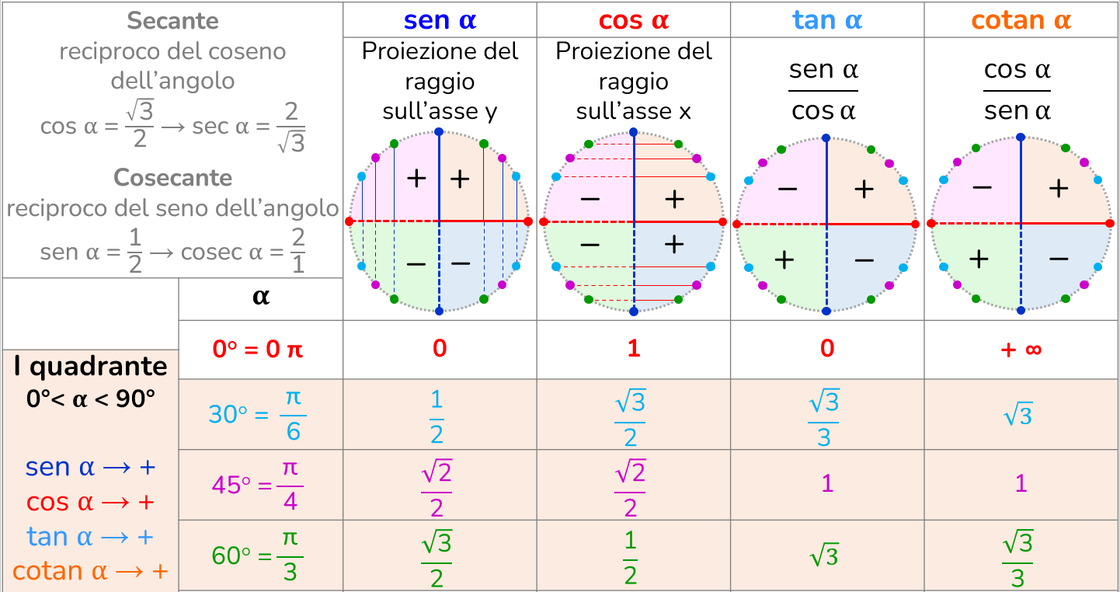
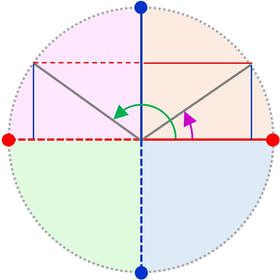
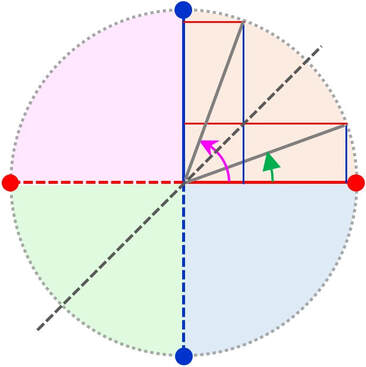
Le funzioni seno e coseno

Coseno → la proiezione del raggio sull'asse delle x (asse delle ascisse)
Seno → la proiezione del raggio sull'asse delle y (asse delle ordinate)

Il valore del seno e del coseno di un qualunque angolo è sempre compreso tra -1 e 1, questo vuol dire che se in un'equazione mi viene richiesto quand'è che il "sen x = 3" la risposta è "impossibile", perché il sen x può essere al massimo uguale a 1.

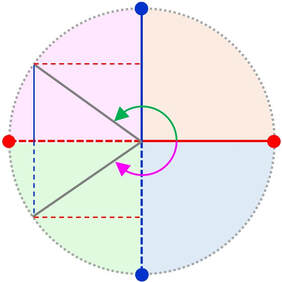
0° < α < 90°
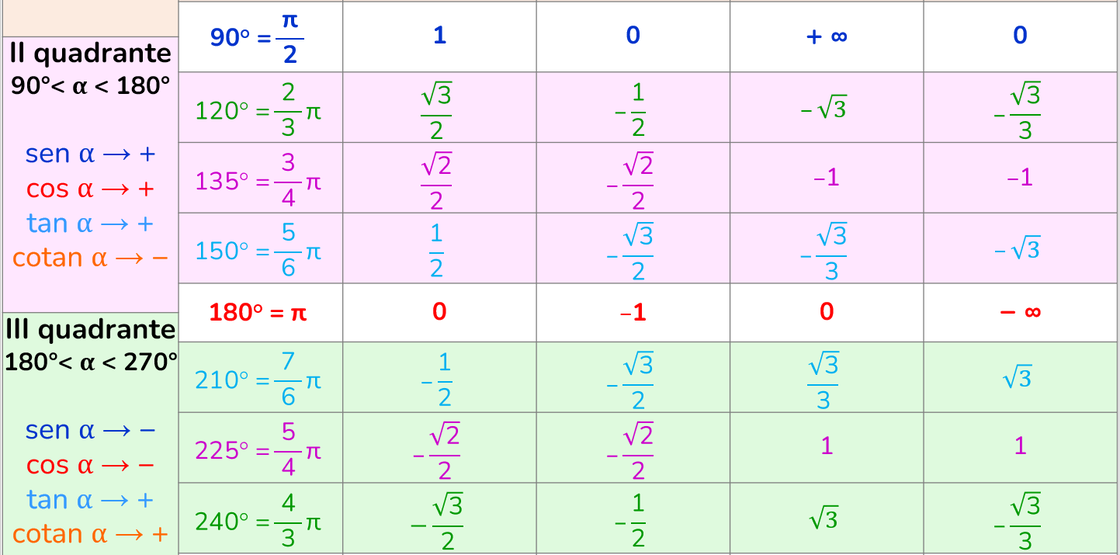
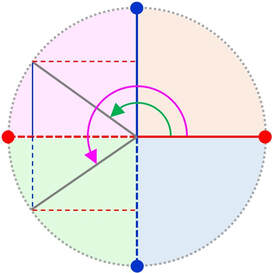
Coseno positivo
Seno positivo

90° < α < 180°
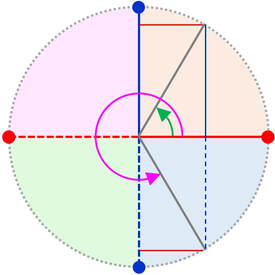
Coseno negativo
Seno positivo

180° < α < 270°
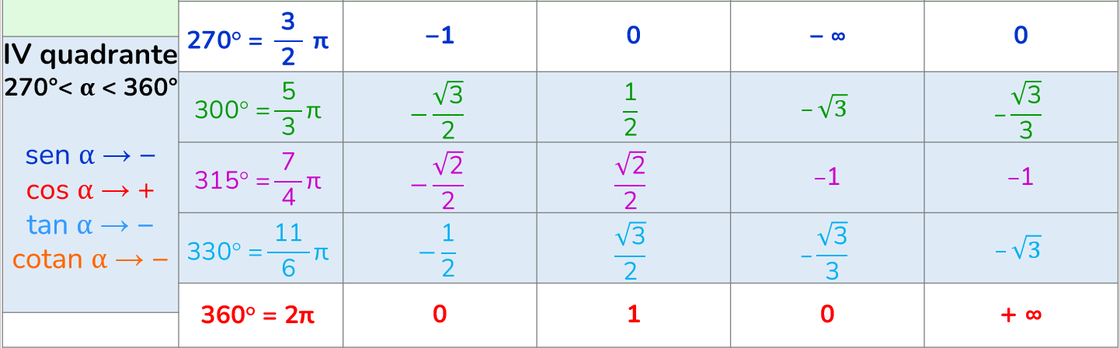
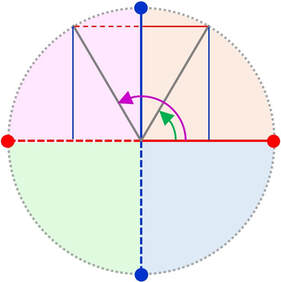
Coseno negativo
Seno negativo

270° < α < 360°
Coseno positivo
Seno negativo

I GRAFICI DELLE FUNZIONI GONIOMETRICHE

La funzione sin x

La funzione sin x è una funzione periodica con ciclo uguale a 2π.

sin x = 0 → x = 0 ± kπ con k ∈ N
sin x = +1 → x = π/2 ± 2kπ con k ∈ N
sin x = –1 → x = –π/2 ± 2kπ con n ∈ N

La funzione sin (x/2)

La funzione sin (x/2) è una funzione periodica con ciclo uguale a 4π.
La funzione sin (x/2) ha stessa ampiezza ma lunghezza d'onda doppia rispetto alla funzione sin x.

sin x/2 = 0 → x = 0 ± 2nπ con n∈N
sin x/2 = +1 → x = π ± 4nπ con n∈N
sin x/2 = –1 → x = –π ± 4nπ con n∈N

La funzione sin 2x

La funzione sin (2x) è una funzione periodica con ciclo uguale a π.
La funzione sin (2x) ha stessa ampiezza ma lunghezza d'onda è la metà rispetto alla funzione sen x.

sin 2x = 0 → x = 0 ± n π/2 con n∈N
sin 2x = +1 → x = π/4 ± nπ con n∈N
sin 2x = –1 → x = –π/4 ± nπ con n∈N

La funzione cos x

La funzione cos x è una funzione periodica con ciclo uguale a 2π.

cos x = 0 → x = π/2 ± nπ con n∈N
cos x = +1 → x = 0 ± 2nπ con n∈N
cos x = –1 → x = π ± 2nπ con n∈N

La funzione cos (x/2)

La funzione cos (x/2) è una funzione periodica con ciclo uguale a 4π.
La funzione cos (x/2) ha stessa ampiezza ma lunghezza d'onda doppia rispetto alla funzione cos x.

cos x/2 = +1 → x = 0 ± 4nπ con n∈N
cos x/2 = 0 → x = π ± 2nπ con n∈N
cos x/2 = –1 → x = 2π ± 4nπ con n∈N

La funzione cos (2x)

Clicca qui per modificare.

cos 2x = +1 → x = 0 ± nπ con n∈N
cos 2x = 0 → x = π/4 ± nπ/2 con n∈N
cos 2x = –1 → x = π/2 ± nπ con n∈N

Le funzioni sin x e cos x a confronto

Le funzioni sin x e cos x sono funzioni periodiche con ciclo uguale a 2π, la differenza di fase è uguale a π/2.

Tangente di x

Tangente di 2x

Tangente di x/2

Seno, coseno, tangente e cotangente nei diversi quadranti

Gli angoli associati α e −α

α → rotazione del raggio in senso antiorario
−α → rotazione del raggio in senso orario

Se α ∈ I quadrante → −α ∈ al IV quadrante
Se α ∈ II quadrante → −α ∈ al III quadrante
Se α ∈ III quadrante → −α ∈ al II quadrante
Se α ∈ IV quadrante → −α ∈ al I quadrante

sen (−α) = − sen α
cos (−α) = cos α
tg (−α) = − tg α
cotg (−α) = − cotg α

Gli angoli associati α e 2π − α → I due angoli sono esplementari

α → rotazione del raggio in senso antiorario
2π − α corrisponde alla posizione del raggio di un angolo uguale a − α visto poco prima

Se α ∈ I quadrante → 2π − α ∈ al IV quadrante
Se α ∈ II quadrante → 2π − α ∈ al III quadrante
Se α ∈ III quadrante → 2π − α ∈ al II quadrante
Se α ∈ IV quadrante → 2π − α ∈ al I quadrante

sen (2π − α) = − sen α
cos (2π − α) = cos α
tg (2π − α) = − tg α
cotg (2π − α) = − cotg α

Gli angoli associati α (con α < 180°) e π − α → I due angoli sono supplementari

α → rotazione del raggio in senso antiorario
π − α corrisponde alla posizione del raggio precedente riflesso rispetto all’asse y

Se α ∈ I quadrante → π − α ∈ al II quadrante
Se α ∈ II quadrante → π − α ∈ al I quadrante

sen (π − α) = sen α
cos (π − α) = – cos α
tg (π − α) = − tg α
cotg (π − α) = − cotg α

Gli angoli associati α (con α < 90°) e π/2 − α → I due angoli sono complementari

α → rotazione del raggio in senso antiorario
π/2 − α corrisponde alla posizione del raggio precedente riflesso rispetto alla bisettrice del I e III quadrante

I due angoli appartengono entrambi al primo quadrante.
I due angoli sono complementari → la loro somma è uguale a 90°

sen (π/2 − α) = cos α
cos (π/2 − α) = sen α
tg (π/2 − α) = cotg α
cotg (π/2 − α) = tg α

Contatore inserito il 12 marzo 2022