POSIZIONI RECIPROCHE DI DUE CIRCONFERENZA
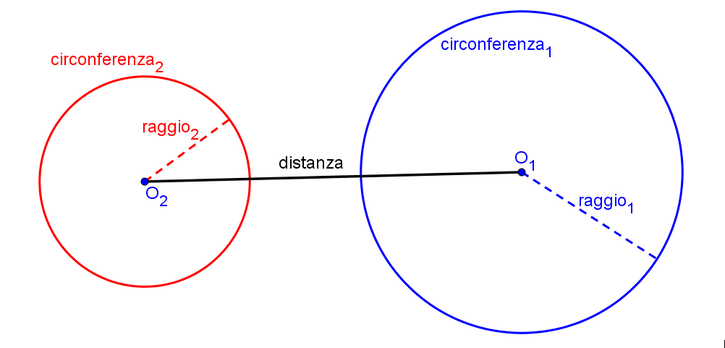
Circonferenze esterne
La distanza tra i loro centri è maggiore della somma dei loro raggi
distanza > r₂ + r₁
Le circonferenze non hanno nessun punto in comune.
distanza > r₂ + r₁
Le circonferenze non hanno nessun punto in comune.
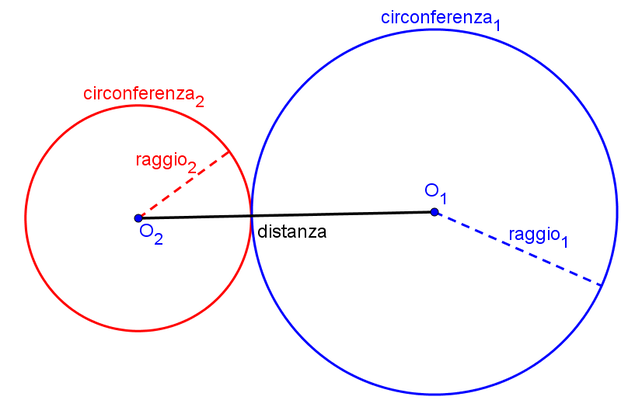
Circonferenze tangenti esterne
La distanza tra i loro centri è uguale alla somma dei loro raggi
distanza = r₁ + r₂
Le due circonferenze hanno un punto in comune.
distanza = r₁ + r₂
Le due circonferenze hanno un punto in comune.
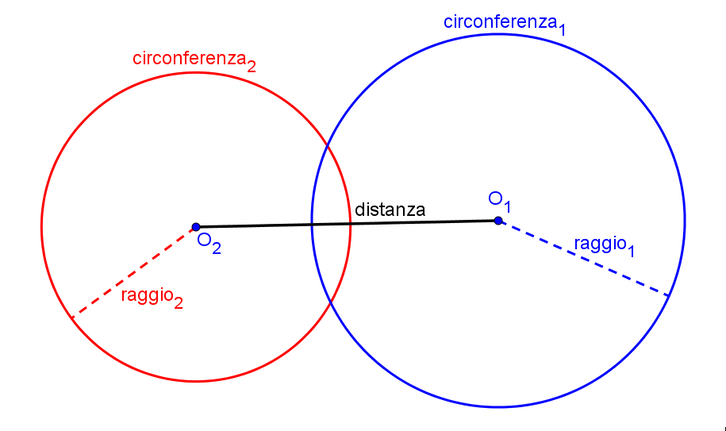
Circonferenze secanti
La distanza tra i loro centri è compresa tra la somma e la differenza dei loro raggi
r₁ - r₂ < distanza < r₁ + r₂
Le due circonferenze hanno due punti in comune.
r₁ - r₂ < distanza < r₁ + r₂
Le due circonferenze hanno due punti in comune.
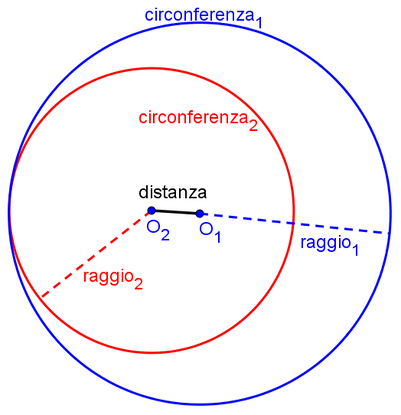
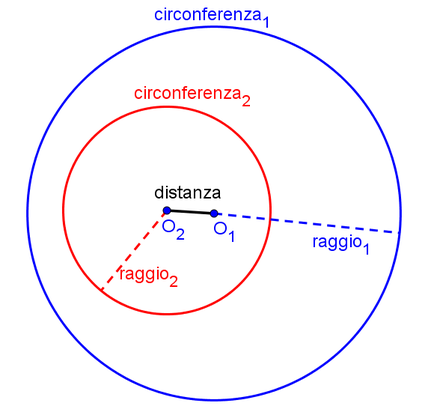
Circonferenze tangenti interne
Circonferenze interne
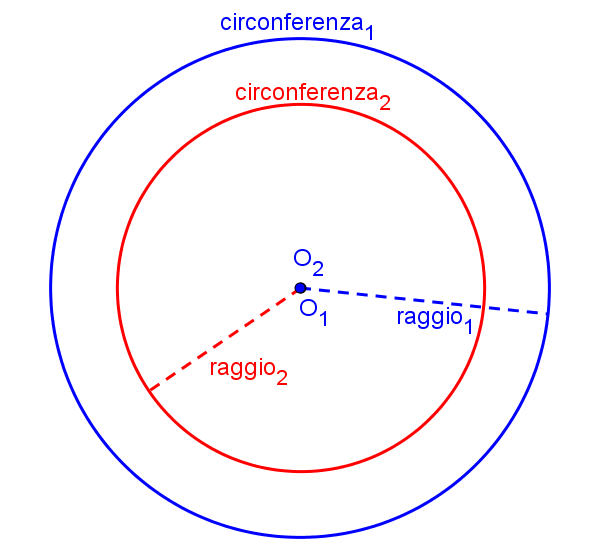
Circonferenze concentriche
Contatore inserito il 30 maggio 2021
Pagina revisionata il 30 maggio 2021
Pagina revisionata il 30 maggio 2021