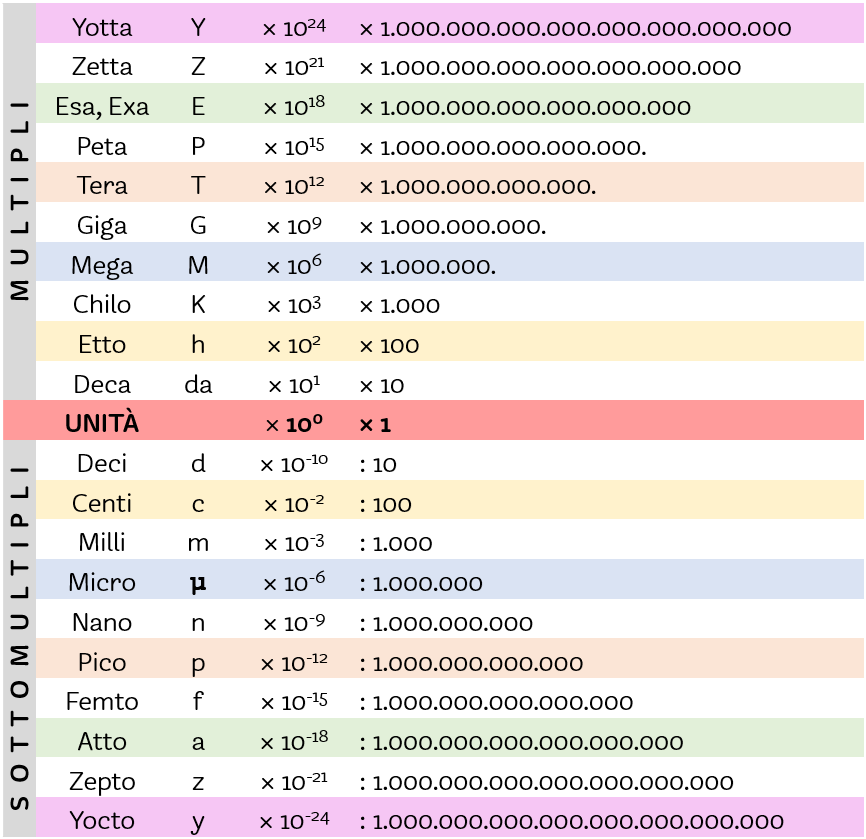
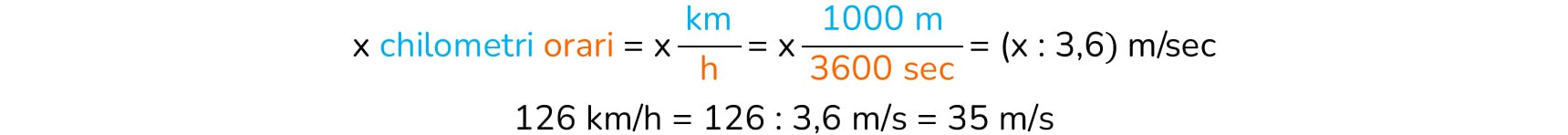LA MISURA E LE UNITÀ DI MISURA
Che cos'è una grandezza?
Una grandezza è una quantità che può essere misurata, in modo diretto o indiretto, utilizzando uno o più strumenti di misura.
Che cos'è un'unità di misura?
Un'unità di misura è una quantità precisa di una grandezza che viene presa come riferimento.
Cosa vuol dire misurare?
Misurare vuol dire confrontare la grandezza con l’unità di misura.
Risponde alla domanda: quante volte l’unità di misura è contenuta nella grandezza che sto misurando?
Per dare una definizione operativa di una grandezza bisogna definire gli strumenti necessari per misurare la grandezza e stabilire un protocollo con cui utilizzare gli strumenti.
Risponde alla domanda: quante volte l’unità di misura è contenuta nella grandezza che sto misurando?
Per dare una definizione operativa di una grandezza bisogna definire gli strumenti necessari per misurare la grandezza e stabilire un protocollo con cui utilizzare gli strumenti.
IL SISTEMA INTERNAZIONALE DI MISURA S.I.
Grandezza |
Unità di misura |
Simbolo |
Strumento |
Lunghezza (distanze, altezze, …) |
metro |
m |
metro, calibro, rotella metrica, ... |
Intervallo di tempo |
secondo 1 minuto = 60 secondi 1 ora = 60 minuti = 3600 secondi |
s |
cronometro |
massa (quantità di materia) |
chilogrammo |
kg |
bilancia a due piatti |
temperatura |
Kelvin (0 K = -273,5 °C – 273,5 K = 0 °C) (gradi K = gradi Celsius –273,5) |
K |
termometro |
intensità di corrente |
Ampere |
A |
amperometro |
intensità luminosa |
candela |
cd |
fotometro |
quantità di sostanza |
mole (1 mole = 6,022 · 10²³ atomi o molecole) |
mol |
Lunghezza
L’unità di misura della lunghezza è il metro, inizialmente era stabilito come la lunghezza di una barra di platino-iridio (un metallo) conservata in una teca nel museo a Sévres, vicino Parigi.
La sua definizione è cambiata con il tempo, ora è definita come la distanza percorsa dalla luce in un intervallo di tempo pari a 1/299792458 secondi, che sarebbe circa la trecentomilionesima parte della distanza percorsa dalla luce in un secondo nel vuoto (in un secondo la luce nel vuoto percorre circa 300000 Km).
La sua definizione è cambiata con il tempo, ora è definita come la distanza percorsa dalla luce in un intervallo di tempo pari a 1/299792458 secondi, che sarebbe circa la trecentomilionesima parte della distanza percorsa dalla luce in un secondo nel vuoto (in un secondo la luce nel vuoto percorre circa 300000 Km).
Intervallo di tempo
L’unità di misura dell’intervallo di tempo è il secondo ed è definito come il tempo impiegato dall’onda elettromagnetica del Cesio a compiere 9 192 631 770 oscillazioni (in un secondo ci sono circa 9 miliardi di oscillazioni).
La massa e il peso
Nel linguaggio comune la massa e il peso si riferiscono alla stessa grandezza, ma dal punto di vista scientifico i due sostantivi indicano cose molto diverse tra loro.
Massa → quantità di materia contenuta da un corpo. È una grandezza fondamentale.
La massa non varia nello spazio, essa rimane sempre la stessa dalla Terra alla Luna, a Marte, allo spazio a gravità zero.
La massa esprime dunque la quantità di materia e si misura con la bilancia a due bracci.
L’unità di misura della massa è il chilogrammo ed è un corpo di un cilindro di platino-iridio.
Se due corpi hanno la stessa massa e vengono posti sui due bracci, essi avranno la stessa distanza dal piano d’appoggio.
Se i due corpi hanno massa diversa quello maggiore avrà distanza minore dal piano d’appoggio e viceversa.
La massa non varia nello spazio, essa rimane sempre la stessa dalla Terra alla Luna, a Marte, allo spazio a gravità zero.
La massa esprime dunque la quantità di materia e si misura con la bilancia a due bracci.
L’unità di misura della massa è il chilogrammo ed è un corpo di un cilindro di platino-iridio.
Se due corpi hanno la stessa massa e vengono posti sui due bracci, essi avranno la stessa distanza dal piano d’appoggio.
Se i due corpi hanno massa diversa quello maggiore avrà distanza minore dal piano d’appoggio e viceversa.
Peso → è una grandezza derivata. Indica la forza con la quale un corpo è attratto da un altro. Sulla Terra questa forza è la forza di gravità e si ottiene moltiplicando la massa per l’accelerazione di gravità presente sulla Terra.
peso = massa × accelerazione di gravità = m · g = forza
dove g = 9,81 m/s²
dove g = 9,81 m/s²
Due corpi aventi la stessa massa avranno due pesi diversi in due ambienti soggetti a forze di gravità diverse: sulla Terra un corpo è molto più pesante che sulla Luna. Un corpo sulla Terra è circa 6 volte più pesante che sulla Luna, se sulla Terra un corpo pesa 60 Kg-peso, sulla Luna peserà 10 Kg-peso.
La misura della temperatura
L’unità di misura della temperatura usata nel Sistema Internazionale è il Kelvin.
Nel mondo sono utilizzate diverse unità di misura diverse dal Kelvin, le più comuni sono:
Nel mondo sono utilizzate diverse unità di misura diverse dal Kelvin, le più comuni sono:
- il grado centigrado
0 °C = 273,15 K → la temperatura alla quale l’acqua passa dallo stato solido a quello liquido o viceversa (alla pressione di 1 atmosfera)
100 °C = 295,15 K → la temperatura alla quale l’acqua passa dallo stato liquido a quello di vapore o viceversa (alla pressione di 1 atmosfera) - il grado Fahrenheit.
Da °C a °F → x °F = 1,8 · y °C + 32 mentre da °F a °C → y °C = (x °F – 32) : 1,8