LE CARATTERISTICHE DELLA SOTTRAZIONE
La sottrazione è l'operazione aritmetica che associa a due numeri, detti minuendo e sottraendo, un terzo numero detto differenza.
Sulla retta orientata, la differenza può essere rappresentata dalla distanza tra le due quantità.
16 – 4 = 12
|
La sottrazione può essere definita come l'operazione inversa dell'addizione.
Quando eseguiamo una sottrazione:
|
Lo zero nella sottrazione
Se il sottraendo è uguale a zero, la differenza è uguale al minuendo
22 – 0 = 22
Se il minuendo è uguale a 0, la differenza non esiste nell'insieme dei numeri naturali, esiste invece nell'insieme dei numeri relativi dove è uguale al sottraendo cambiato di segno.
0 – 31 = – 31
Da quanto appena detto:
lo zero non è l'elemento neutro nella sottrazione.
lo zero non è l'elemento neutro nella sottrazione.
La sottrazione in colonna
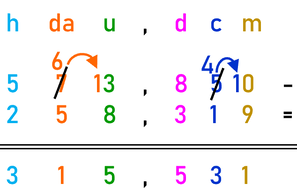
Proviamo ad eseguire insieme la differenza di due numeri decimali: 573,85 – 258,319
Per avere la stessa quantità di cifre decimali aggiungi degli zeri: 573,850 – 258,319
Per avere la stessa quantità di cifre decimali aggiungi degli zeri: 573,850 – 258,319
- metti in colonna i due numeri, mettendo sulla stessa verticale le virgole e le cifre dello stesso peso (unità sotto le unità, decine sotto le decine, ...)
- parti dalla colonna più a destra, togli alla cifra sopra quella sotto
- se la sottrazione è possibile scrivi il risultato sotto
- se la sottrazione non è possibile chiedi un prestito alla cifra alla sua sinistra (che diminuisce il suo valore di 1).
Vediamo una sottrazione nella quale il prestito è richiesto allo zero.
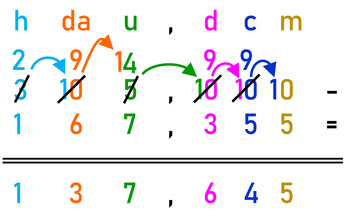
Quella che vi propongo sotto è una sottrazione piuttosto complessa:
305 – 167,355
Innanzitutto mettiamo la virgola e tre zeri decimali al primo numero, la sottrazione diverrà così: 305,000 – 167,355
Come sappiamo, anche le sottrazioni vanno iniziate dalle cifre più a destra:
305 – 167,355
Innanzitutto mettiamo la virgola e tre zeri decimali al primo numero, la sottrazione diverrà così: 305,000 – 167,355
Come sappiamo, anche le sottrazioni vanno iniziate dalle cifre più a destra:
- vorremo togliere il 5 allo zero, non si può fare
- così lo zero chiede un prestito alla cifra al suo fianco, ma è uno zero
- allora anche questo zero chiede un prestito alla cifra al suo fianco, ma anche lui è uno zero
- allora anche questo zero chiede un prestito alla cifra al suo fianco, un 5
- il 5 dà una decina allo zero nei decimi, diventando un 4
- il 10 appena formato diventa un 9 e può dare una decina allo zero dei centesimi,
- il 10 ora formato diventa un 9 e può dare una decina allo zero dei millesimi.
- colonna dei millesimi: 10 – 5 = 5 e lo scriviamo sotto
- colonna dei centesimi: 9 – 5 = 4 e lo scriviamo sotto
- colonna dei decimi: 9 – 3 = 6 e lo scriviamo sotto
- colonna delle unità: 4 – 7 = non si può fare, allora si chiede un prestito alla cifra al suo fianco, ma è uno zero che chiederà a sua volta alla cifra alla sua sinistra, che è un 3
- il 3 diventa un 2 e fa diventare lo zero delle decine un 10 che a sua volta diventa un 9 donando una decina al 4 che diventa 14.
- colonna delle unità: 14 – 7 = 7 e lo scriviamo sotto
- colonna delle decine: 9 – 6 = 3 e lo scriviamo sotto
- colonna delle centinaia: 2 – 1 = 1 e lo scriviamo sotto.
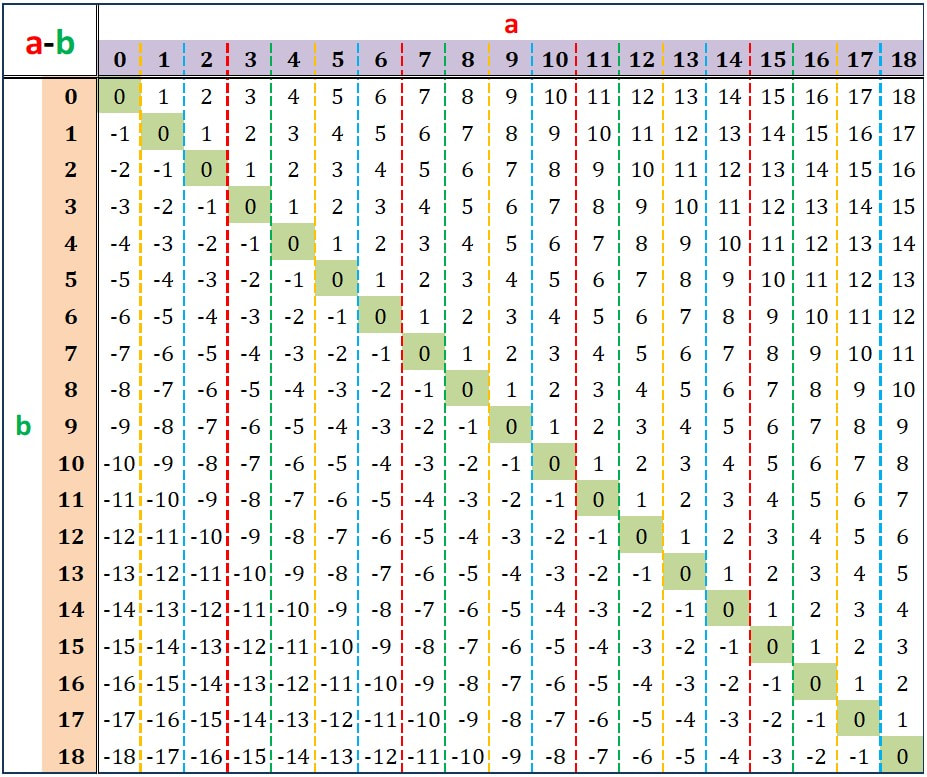
Tavola della sottrazione
Nota Bene: i risultati sono positivi al di sopra della diagonale formata da zeri, e invece negativi al di sotto della stessa diagonale.
Possiamo dire che la tabella è simmetrica rispetto alla diagonale rossa, a meno del segno, ad indicare che la differenza, in valore assoluto rimane la stessa, ma ad essa si attribuisce il segno del più grande.
Possiamo dire che la tabella è simmetrica rispetto alla diagonale rossa, a meno del segno, ad indicare che la differenza, in valore assoluto rimane la stessa, ma ad essa si attribuisce il segno del più grande.
Le operazioni inverse della sottrazione o la loro prova
PROPRIETÀ DELLA SOTTRAZIONE
Proprietà invariantiva (invariare = che non cambia)
Addizionando o sottraendo (aggiungendo o togliendo) una stessa quantità (lo stesso numero) sia al minuendo che al sottraendo la differenza non cambia.
La sottrazione nei problemi
|
Rispondo alle domande
Qual è la differenza…? Qual è il resto …? Quanti in più …? Quanti non …? Quanti … in meno? Quanto rimane …? Quanti rimangono …? Quanti mancano …? Quanto resta …? |
Quali azioni devo compiere?
Faccio un confronto Scopro quanto manca Scopro la differenza Tolgo Sottraggo Scopro il resto |