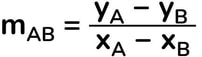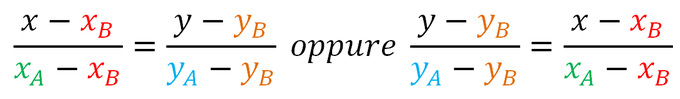LA RETTA E LA SUA EQUAZIONE
L'equazione di una rettaOgni retta disegnata nel piano cartesiano ha un’equazione che la identifica in modo unico.
In generale le equazioni delle rette possono essere scritte in modi diversi ma via via vedremo i diversi casi: in tutte compare sempre almeno una lettera, o la x o la y o entrambe, e c’è sempre un numero (compreso lo zero, perché anche lui è un numero). |
Rette parallele agli assi cartesiani
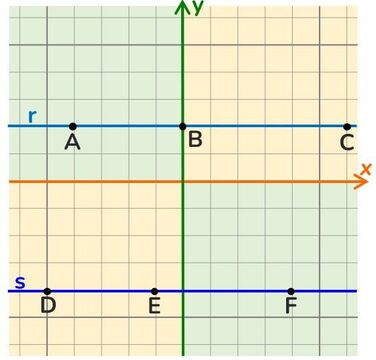
Rette parallele all’asse x
Sono rette i cui punti hanno sempre la stessa distanza dall’asse delle ascisse (o asse delle x).
Il punto di incontro tra l’asse delle y e la retta definisce l’ordinata di tutti i punti della retta.
Ogni punto appartenente ad una retta parallela all’asse x ha sempre lo stesso valore delle ordinate.
Ogni punto della retta r ha come coordinate (x; 2) → la sua equazione è y = 2.
Ogni punto della retta s ha come coordinante (x; -4) → la sua equazione è y = -4.
L’asse delle x ha come equazione: y = 0
Sono rette i cui punti hanno sempre la stessa distanza dall’asse delle ascisse (o asse delle x).
Il punto di incontro tra l’asse delle y e la retta definisce l’ordinata di tutti i punti della retta.
Ogni punto appartenente ad una retta parallela all’asse x ha sempre lo stesso valore delle ordinate.
Ogni punto della retta r ha come coordinate (x; 2) → la sua equazione è y = 2.
Ogni punto della retta s ha come coordinante (x; -4) → la sua equazione è y = -4.
L’asse delle x ha come equazione: y = 0
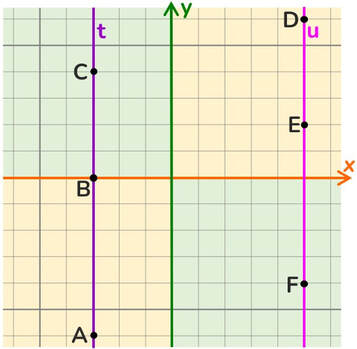
Rette parallele all’asse y
Sono rette i cui punti hanno sempre la stessa distanza dall’asse delle ordinate (o asse delle y).
Il punto di incontro tra l’asse delle x e la retta definisce l’ordinata di tutti i punti della retta.
Ogni punto appartenente ad una retta parallela all’asse y ha sempre lo stesso valore delle ascisse.
Ogni punto della retta t ha come coordinate (-3; y) → la sua equazione è x = -3.
Ogni punto della retta u ha come coordinante (5; y) → la sua equazione è x = 5.
L’asse delle y ha come equazione x = 0
Sono rette i cui punti hanno sempre la stessa distanza dall’asse delle ordinate (o asse delle y).
Il punto di incontro tra l’asse delle x e la retta definisce l’ordinata di tutti i punti della retta.
Ogni punto appartenente ad una retta parallela all’asse y ha sempre lo stesso valore delle ascisse.
Ogni punto della retta t ha come coordinate (-3; y) → la sua equazione è x = -3.
Ogni punto della retta u ha come coordinante (5; y) → la sua equazione è x = 5.
L’asse delle y ha come equazione x = 0
Rette passanti per l’origine degli assi
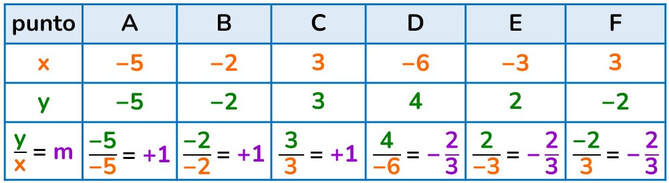
Le rette passanti nell’origine degli assi le abbiamo già viste quando abbiamo analizzato la proporzionalità diretta. Come vedremo con alcuni esempi il rapporto tra la coordinata y e quella x di ciascun punto che gli appartiene è sempre uguale.
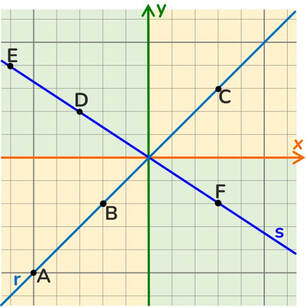
Il rapporto tra l’ordinata e l’ascissa di ciascun punto della retta r è +1, da questo deriva che la sua equazione è y = 1x o semplicemente y = x (in questo caso particolare ogni punto ha come ordinata e ascissa esattamente la stessa quantità).
Il rapporto tra l’ordinata e l’ascissa di ciascun punto della retta s è -2/3, da questo deriva che la sua equazione è y = -2/3 x.
Il valore del rapporto tra l’ordinata e l’ascissa di ogni punto nelle rette passanti per l’origine prende il nome di coefficiente angolare m, in quanto dà un’indicazione sull’orientamento e sulla pendenza che la retta ha rispetto all’asse delle x.
Il rapporto tra l’ordinata e l’ascissa di ciascun punto della retta s è -2/3, da questo deriva che la sua equazione è y = -2/3 x.
Il valore del rapporto tra l’ordinata e l’ascissa di ogni punto nelle rette passanti per l’origine prende il nome di coefficiente angolare m, in quanto dà un’indicazione sull’orientamento e sulla pendenza che la retta ha rispetto all’asse delle x.
|
m positivo
Disegnando la retta da sinistra verso destra i valori sia delle ascisse che delle ordinate
diventano maggiori. Sono rette che tagliano il I e il III quadrante. |
m negativo
Disegnando la retta da sinistra verso destra i valori delle ascisse aumentano mentre quelle delle ordinate diminuiscono.
Sono rette che tagliano il II e il IV quadrante. |
Il valore del rapporto tra l’ordinata e l’ascissa di ogni punto nelle rette passanti per l’origine prende il nome di coefficiente angolare m, in quanto dà un’indicazione sull’orientamento (positivo → salita, negativo → discesa) e sulla pendenza che la retta ha rispetto all’asse delle x.
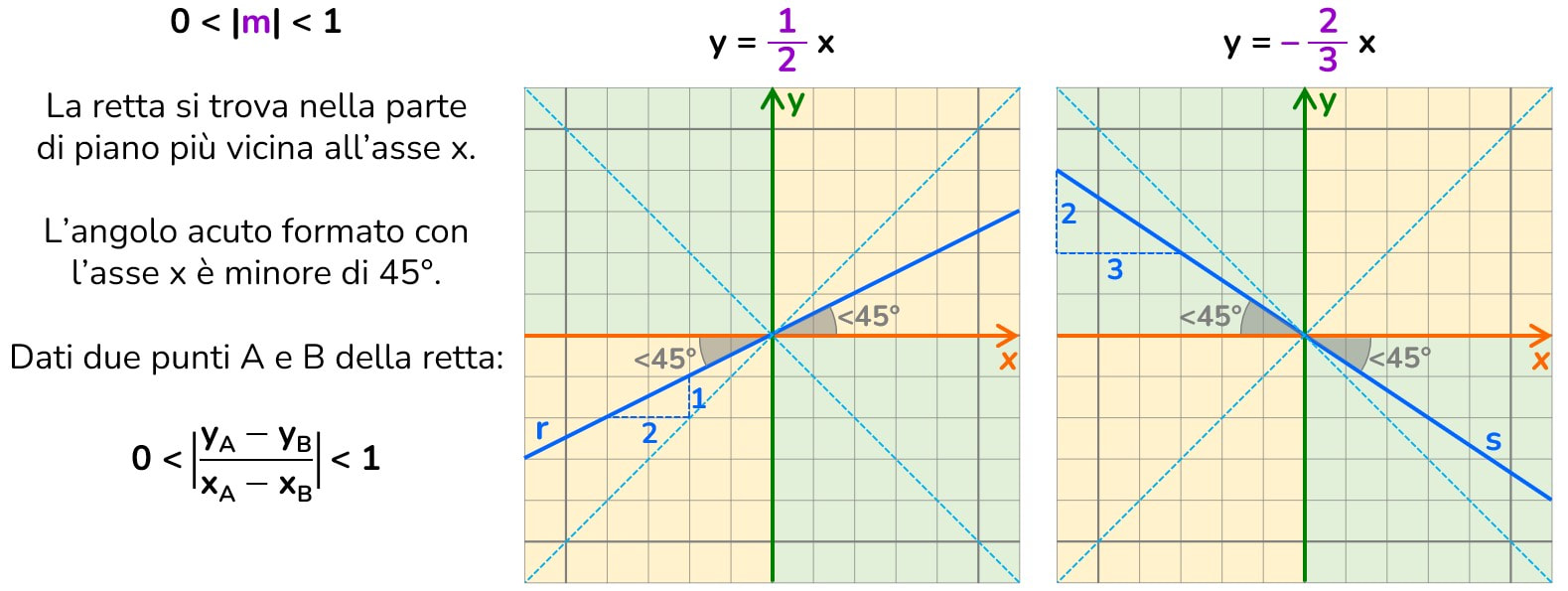
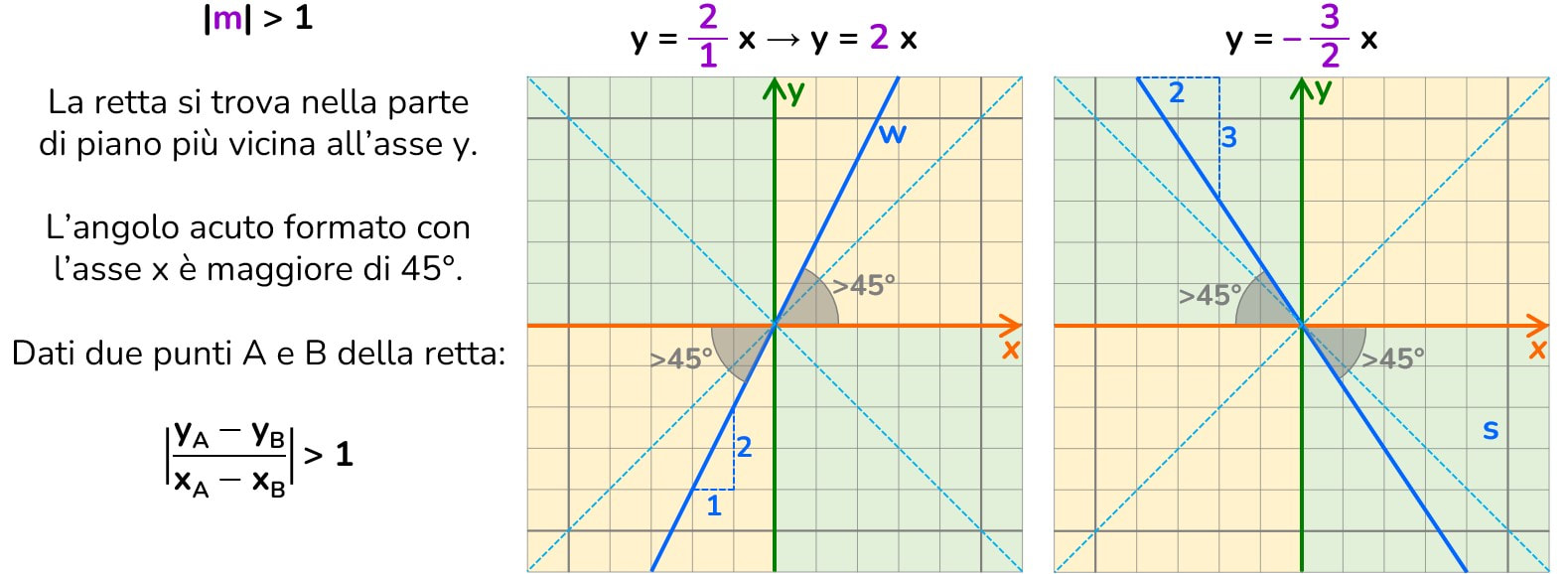
Se consideriamo il valore del coefficiente angolare, senza considerare il segno possiamo notare che se il coefficiente angolare:
Se consideriamo il valore del coefficiente angolare, senza considerare il segno possiamo notare che se il coefficiente angolare:
- è una frazione propria (numeratore < denominatore)
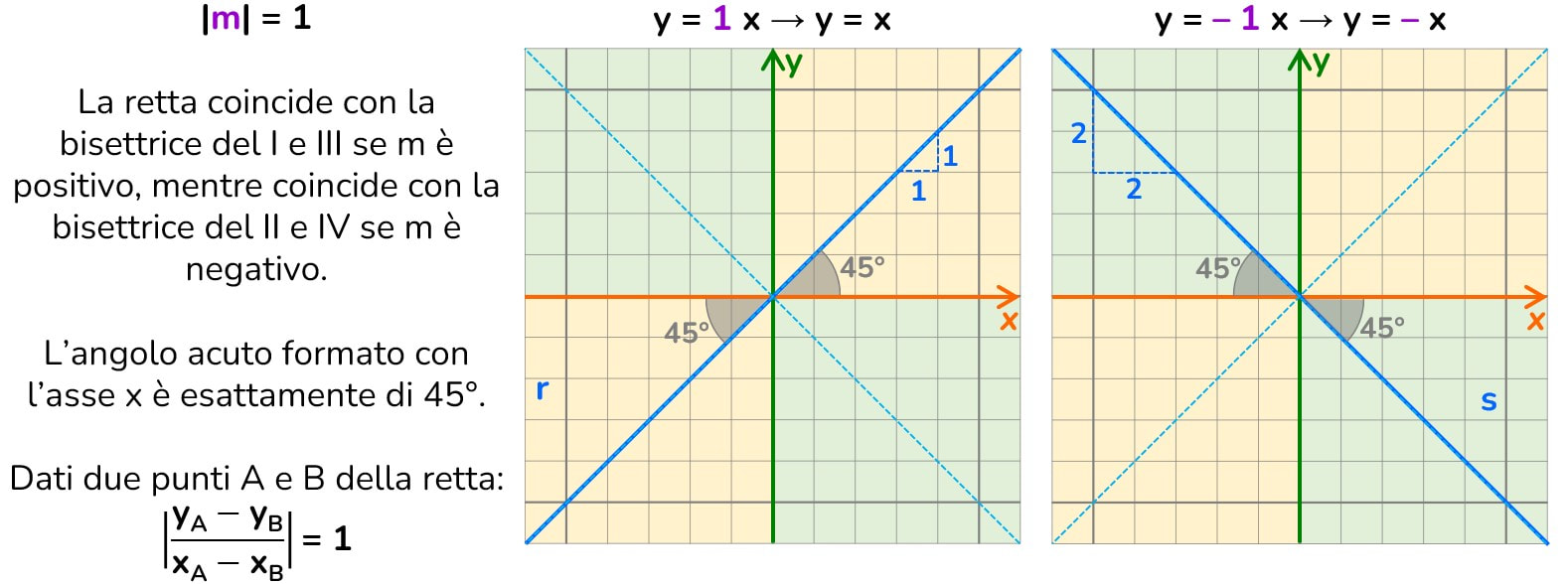
La retta ha una bassa pendenza, forma con l’asse delle x un angolo minore di 45°. - è uguale a 1
È bisettrice del I e III quadrante se m è positivo.
È bisettrice del II e IV quadrante se m è negativo. - è una frazione impropria > 1 (numeratore > denominatore)
La retta ha una pendenza elevata, forma con l’asse delle x un angolo maggiore di 45°.
Vediamo ora in questa tabella in che modo si comporta la retta con i diversi valori del coefficiente angolare m.
|m| → vuol dire che consideriamo il valore assoluto del coefficiente angolare m, senza il segno, al quale invece sono dedicate due colonne separate nella tabella sotto.
|m| → vuol dire che consideriamo il valore assoluto del coefficiente angolare m, senza il segno, al quale invece sono dedicate due colonne separate nella tabella sotto.
L’equazione di una retta generica
Una retta che non è parallela agli assi e non passa per l’origine degli assi cartesiani.
L’equazione generica è scritta in generale in una delle due forme:
L’equazione generica è scritta in generale in una delle due forme:
ax + by + c = 0 → equazione della retta in forma implicita
y = mx + q → equazione della retta in forma esplicita
Per passare dalla forma implicita a quella esplicita basta isolare la y al I membro dell’equazione e poi dividere il secondo membro per il coefficiente della y quando questo è diverso da +1.
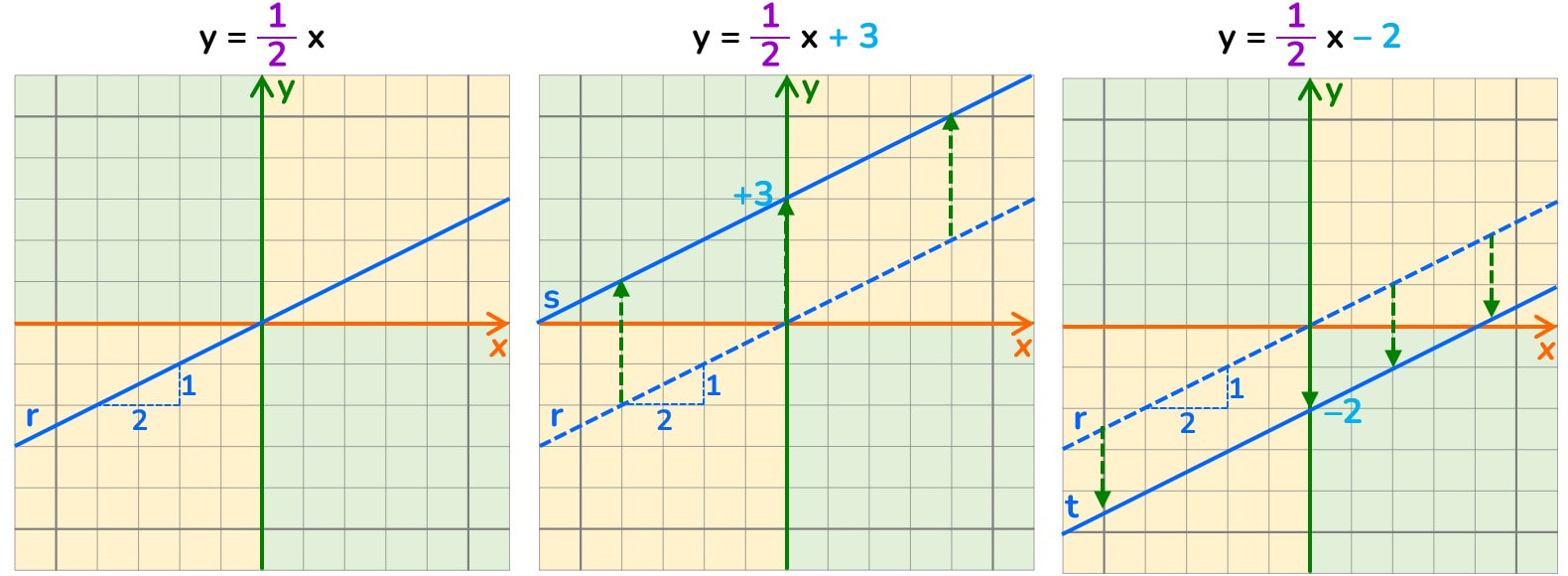
Nell’equazione esplicita della retta:
Nell’equazione esplicita della retta:
m → coefficiente angolare
q → intercetta.
Rappresenta il punto nell’asse y che interseca la retta.
Rappresenta il punto nell’asse y che interseca la retta.
Quando pensiamo alla rappresentazione grafica della retta come prima cosa non consideriamo l’intercetta ma le altre informazioni date dal coefficiente angolare, dopo immaginiamo di traslare la retta, senza nessuna rotazione, sino al punto indicato dal punto di intersezione q.
Dall’equazione di una retta alla sua rappresentazione nel piano cartesiano
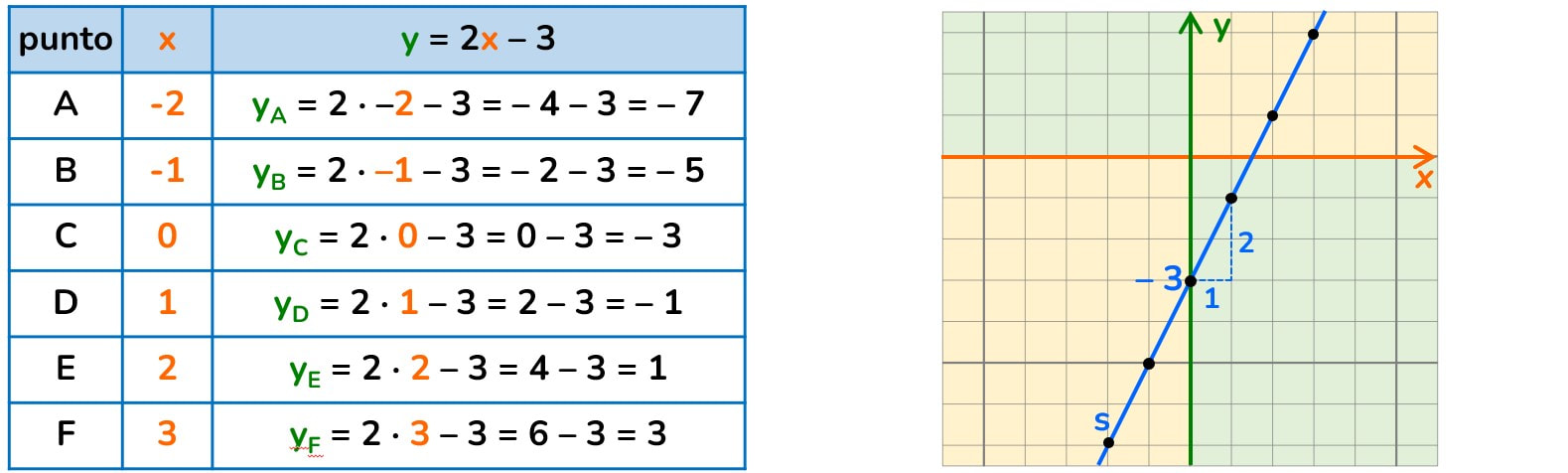
Se di una retta, o di una qualunque funzione, ho la sua equazione, sostituendo ad una delle due lettere un qualsiasi valore a scelta, siamo in grado di conoscere le coordinate di alcuni dei suoi punti.
In linea generale si compila una tabella di valori nella quale nella prima colonna è dato il valore della x scelto e nella seconda colonna il valore della y calcolato sostituendo la x all’equazione.
Vediamo un esempio: Mettiamo i punti nel piano cartesiano:
In linea generale si compila una tabella di valori nella quale nella prima colonna è dato il valore della x scelto e nella seconda colonna il valore della y calcolato sostituendo la x all’equazione.
Vediamo un esempio: Mettiamo i punti nel piano cartesiano:
Equazione della retta passante per due punti A e B
Per trovare l'equazione della retta AB posso usare indistintamente una delle due formule sotto:
userò quest'altra formula se è mia intenzione scrivere l'equazione della retta in forma esplicita: