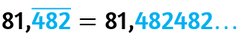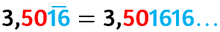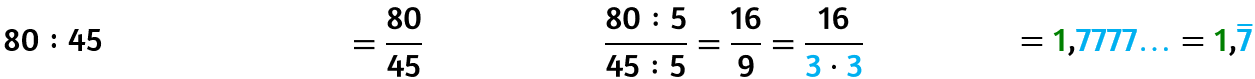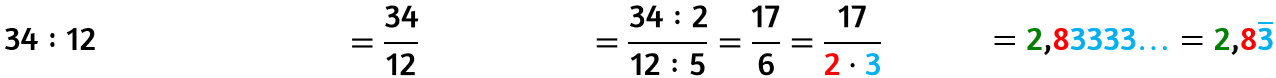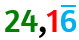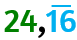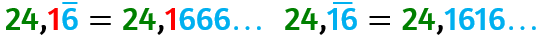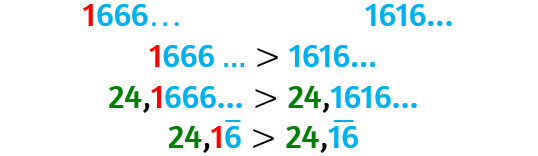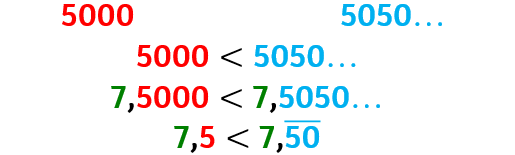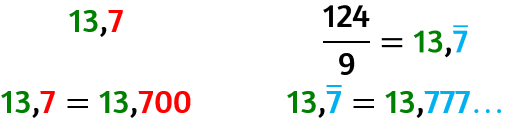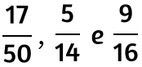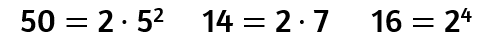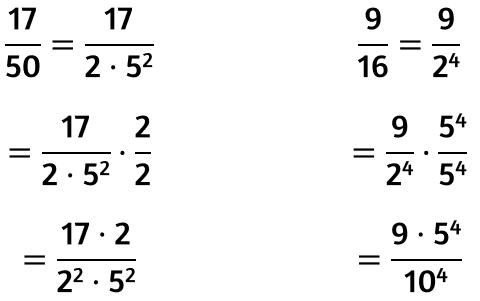I NUMERI RAZIONALI E LE LORO FRAZIONI GENERATRICI

Un numero razionale è un numero decimale che si ottiene da una divisione:
  • tra due numeri interi;
  • nella quale il dividendo non è multiplo del divisore.
Tutti i numeri decimali che possono essere scritti come frazioni sono sicuramente razionali.
Anche i numeri naturali sono numeri razionali perché possono essere scritti come frazioni con denominatore uguale a 1. 
I numeri razionali possono essere di tre tipi:
1.
Numeri decimali limitati
Le cifre dopo la virgola si possono contare.
2.
 Foto
Numeri decimali periodici semplici
Le cifre dopo la virgola sono infinite e si ripetono ciclicamente nello stesso ordine.
Il gruppo di cifre che si ripete si chiama periodo.
Il periodo inizia subito dopo la virgola.
3.
Numeri decimali periodici misti
Le cifre dopo la virgola sono infinite e solo una parte si ripete ciclicamente nello stesso ordine.
Tra la virgola e il periodo ci sono da una a più cifre non periodiche.

Forma sintetica e forma estesa di un numero razionale

Foto
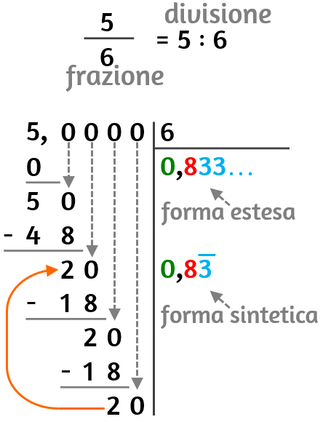
Forma estesa → è quella che compare nella calcolatrice quando calcolo il valore di una divisione. Se il risultato della divisione ha una quantità di cifre decimali tali da riempire tutto il display della calcolatrice, mi devo ricordare di non considerare l’ultima cifra, che può essere approssimata per eccesso e quindi essere ingannevole sull’interpretazione del dato numerico.
Quando eseguo una divisione in colonna ottengo la forma estesa proseguendo la divisione, anche quando le cifre del dividendo sono finite ma il resto è diverso da zero.
​Se dopo diversi passaggi il resto della divisione:
  • diventa zero, il numero che ottengo ha un numero di cifre decimali limitate;
  • non diventa zero, proseguendo la divisione ad un certo punto vedrai ripresentarsi una stessa situazione. Quando questo accade si dice che il numero è periodico e dopo aver scritto alcune cifre, si mettono dei puntini di sospensione, che indicano il loro proseguo.
Forma sintetica → si utilizza per i numeri periodici, la parte periodica è sovrastata da una lineetta orizzontale. ​

Le parti di un numero razionale e come si usano nelle frazioni generatrici

Dal numero decimale alla sua frazione generatrice

NUMERATORE
scrivi tutto il numero togli la parte non periodica 
(nei decimali limitati non dovrai togliere nulla)
DENOMINATORE
nei decimali limitati
Un 1 seguito da tanti zeri quante sono le cifre decimali
nei decimali periodici semplici e misti
Tanti 9 quante sono le cifre periodiche poi
tanti zeri quante sono le cifre dell’antiperiodo
Dopo aver scritto la frazione generatrice, ricordati di semplificarla dividendo numeratore e denominatore per una stessa quantità, fino a quando non saranno primi tra loro.
VEDIAMO LE FRAZIONI GENERATRICI NEI TRE DIVERSI TIPI DI DECIMALI
a.
Numeri decimali limitati
b.
Numeri decimali periodici semplici
c.
Numeri decimali periodici misti

Dalla frazione al tipo di decimale senza eseguire la divisione

È possibile prevedere quale tipo di numero darà origine la divisione senza doverla eseguire?
Assolutamente sì. Ma per poterlo capire dovrai:
  1. scrivere la divisione come frazione e ridurla ai minimi termini (dividendo entrambi i termini per una stessa quantità diverse da zero e uno, fino a quando non è più possibile), in questo modo dividendo e divisore saranno primi tra loro; 
  2. scomporre in fattori primi il divisore (se hai scritto una divisione) o il denominatore (se hai scritto la divisione come una frazione).
Se il denominatore/divisore scomposto in fattori primi avrà:
a.
solo potenze di 2 e/o di 5 → Numeri decimali limitati
divisione
frazione
frazione semplificata
quoziente
b.
solo potenze DIVERSE da 2 e/o 5 → Numeri decimali periodici semplici
divisione
frazione
frazione semplificata
quoziente
c.
sia potenze di 2 e/o 5 che potenze DIVERSE da 2 e/o 5 → Numeri decimali periodici misti
divisione
frazione
frazione semplificata
quoziente

Confrontare i numeri razionali dati come decimali o come frazioni 

Se due numeri decimali, di qualunque tipo essi siano, hanno parte intera diversa, sarà maggiore il numero che ha parte intera maggiore.
Confrontare numeri decimali limitati tra loro aventi stessa parte intera
Chi è il maggiore tra 5,16 e 5,5?
  1. Riscrivi i due numeri con la stessa quantità di cifre decimali.
  2. Poiché la parte intera è uguale dovrai confrontare la parte decimale.
  3. La parte decimale maggiore, composta dalla stessa quantità di cifre decimali, sarà abbinata al numero decimale maggiore.
Confrontare numeri periodici semplici e/o misti aventi stessa parte intera
Dentro la parentesi sono indicate le cifre periodiche.
Chi è il maggiore tra 24,1(6) e 24,(16)?
  1. Riscrivi i due numeri con la stessa quantità di cifre decimali.
  2. Poiché la parte intera è uguale dovrai confrontare la parte decimale.
  3. La parte decimale maggiore, composta dalla stessa quantità di cifre decimali, sarà abbinata al numero decimale maggiore.
confronta solo la parte decimale  
Confrontare numeri decimali periodici e numeri decimali limitati aventi stessa parte intera
Chi è il maggiore tra 7,5 e 7,(50)?
  1. Riscrivi i due numeri con la stessa quantità di cifre decimali.
  2. Poiché la parte intera è uguale dovrai confrontare la parte decimale.
  3. La parte decimale maggiore, composta dalla stessa quantità di cifre decimali, sarà abbinata al numero decimale maggiore.
parte decimale
Confrontare numeri decimali e frazioni
Chi è il maggiore tra 13,7 e 124/9?
  1. Trasforma la frazione in numero decimale eseguendo la divisione tra numeratore e denominatore.
  2. Riscrivi i due numeri con la stessa quantità di cifre decimali.
  3. Poiché la parte intera è uguale dovrai confrontare la parte decimale.
  4. La parte decimale maggiore, composta dalla stessa quantità di cifre decimali, sarà abbinata al numero decimale maggiore.
parte decimale

Trasformare una frazione in un numero decimale limitato senza eseguire la divisione

Come abbiamo visto, non tutte le frazioni danno origine a numeri decimali limitati.
Per poter trasformare una frazione in un numero decimale limitato, la frazione, ridotta ai minimi termini deve avere al denominatore un numero che ha, nella sua scomposizione in fattori primi, solo potenze di 2 e/o di 5.
Supponiamo di avere le seguenti frazioni e di volerle trasformare nei corrispondenti numeri decimali limitati.
1.
Scomponi in potenze di fattori primi il denominatore
2.
Il denominatore scomposto è formato solo da potenze di 2 e/o 5?
  • sì → puoi scrivere la frazione come numero decimale limitato
  • no → non puoi scrivere la frazione come numero decimale limitato 
sì
no
sì
3.
Se sì moltiplica numeratore e denominatore per una potenza così formata:
  • base → la potenza con esponente minore o quella assente (che sarà o 2 o 5)
  • esponente → la differenza tra l’esponente maggiore e quello minore (che sarà 0 nel caso una potenza fosse assente)
In questo modo sia il 2 che il 5 al denominatore avranno lo stesso esponente.
4.
Risolvi le singole potenze e risolvi le moltiplicazioni sia al numeratore che al denominatore
5.
Riscrivi il numeratore e metti una virgola di modo da lasciare dopo la virgola tante cifre decimali quanti sono gli zeri della potenza di 10 al denominatore.

Le espressioni con i numeri razionali

Espressioni con numeri interi e numeri decimali limitati
Per poter svolgere un’espressione composta sia da numeri interi che da numeri decimali limitati puoi seguire due strade: 
  1. svolgere l’espressione così come hai visto nella classe prima.
  2. trasformare i numeri decimali limitati nelle loro frazioni generatrici e risolverla come qualunque espressione formata da numeri interi e frazioni.
Espressioni con numeri decimali limitati, periodici e/o frazioni
Per poter svolgere un’espressione composta sia da numeri decimali limitati che da numeri decimali periodici è importante trasformare i numeri decimali nelle loro frazioni generatrici.
Questo è importante perché se lasciassi i numeri decimali limitati e periodici così come sono, la domanda che ti dovresti porre è: quante cifre dovrei prendere in considerazione?
Qualunque sia il numero di cifre che prenderai in considerazione il risultato sarà sempre approssimato.
Il modo più corretto e preciso per svolgere un’espressione con numeri decimali periodici con o senza altri numeri decimali limitati o numeri interi è SEMPRE quello di trasformare i numeri decimali in frazioni e risolvere l’espressione così come hai visto in precedenza.