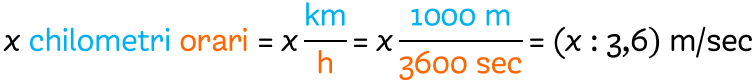|
Esprimere una certa misura con diverse unità di misura è importante, perché ci aiuta a capire meglio il valore di una certa misura.
Vi immaginate un cartello, nelle strade extraurbane, che esprime le distanze in decimetri? Nel leggere il cartello si rischierebbe di avere un incidente stradale. Ma, state tranquilli, le distanze, nei cartelli stradali presenti nelle strade extraurbane, sono espresse in chilometri. |
Lei si trova a 37425 dm di distanza
Lei si trova a 3,7 km di distanza
|
Oppure immaginate di esprimere il lato di un quadretto del vostro quaderno in chilometri (0,000005 km), quanto sarebbe difficile leggere questa misura e saperla interpretare?
* Lei è un comune italiano di 472 abitanti della provincia di Nuoro che sorge su una serie di colline poste a circa 500 m s.l.m.
* Lei è un comune italiano di 472 abitanti della provincia di Nuoro che sorge su una serie di colline poste a circa 500 m s.l.m.
Le equivalenze tra misure lineari
Ogni cifra, in una misura, rappresenta un’unità di misura diversa.
- Nella misura 3,5 m: 3 sono le unità di metri 5 sono le unità di decimetri
- Nella misura 3,5 hm: 3 sono le unità di ettometri 5 sono le unità di decametri
Fare un’equivalenza → esprimere una stessa misura utilizzando unità di misura diverse.
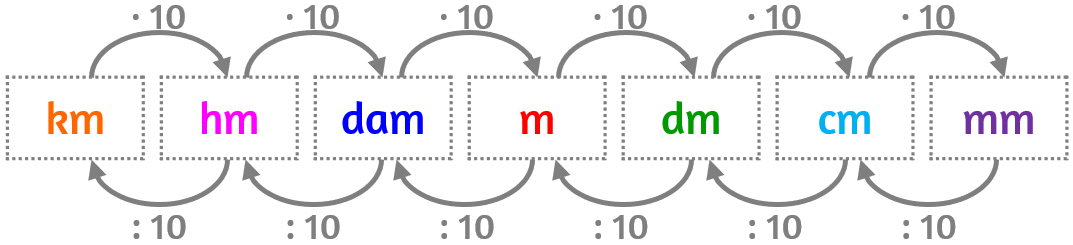
Il salto da un’unità di misura ad un’altra al suo fianco genera sempre un cambiamento:
- aumenta di 10 volte con ogni salto che compio verso destra
- diminuisce di 10 volte con ogni salto che compio verso sinistra
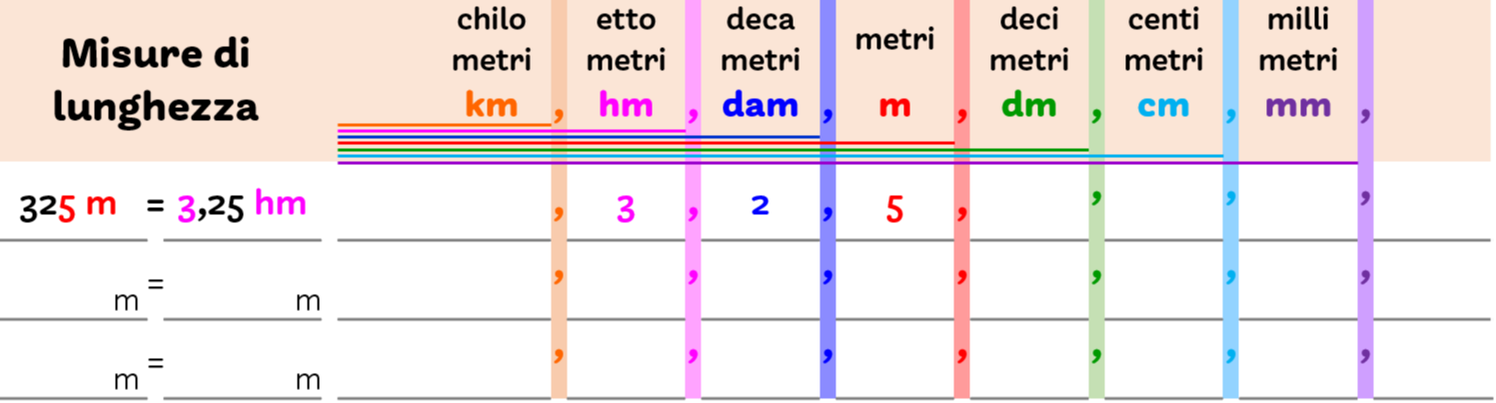
Individua la cifra delle unità e scrivila nella colonna dell’unità di misura indicata.
Per leggere il risultato in un’altra unità di misura usa la virgola che si trova alla sua destra.
Per leggere il risultato in un’altra unità di misura usa la virgola che si trova alla sua destra.
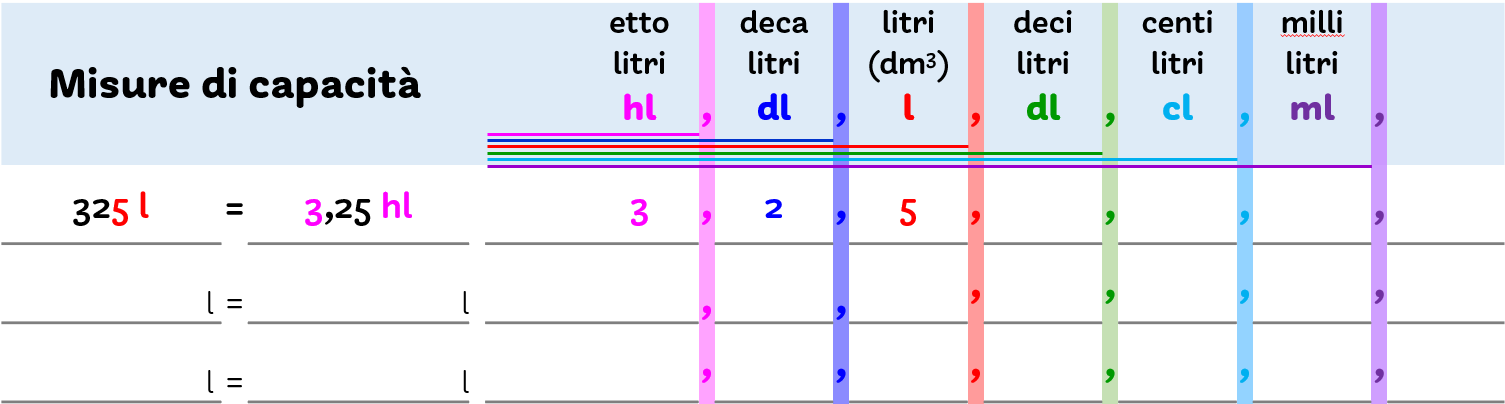
Allo stesso modo ci comporteremo per le misure di capacità:
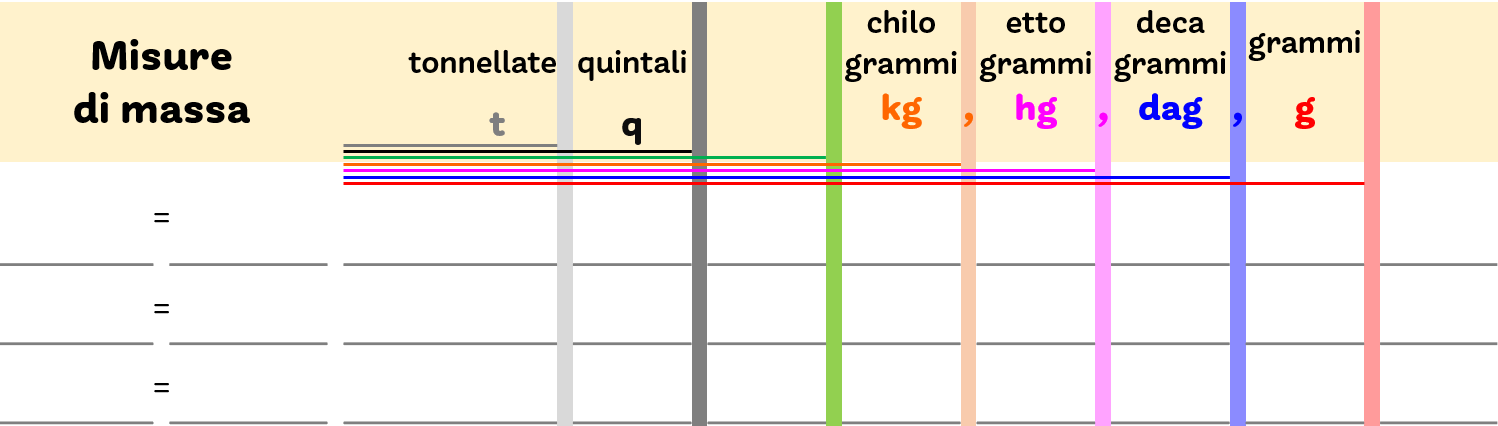
Ecco uno schema per le misure di massa:
Per le misure di massa, nel linguaggio comune, sono utilizzati altri due multipli: il quintale che corrisponde a 100 kg e la tonnellata che corrisponde a 1000 kg.
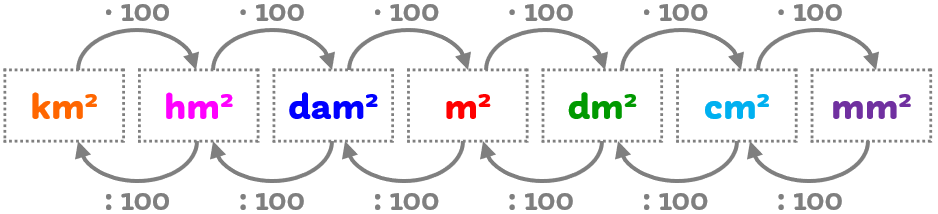
Le equivalenze tra le misure di superficie
Il salto da un’unità di misura ad un’altra al suo fianco genera sempre un cambiamento che è uguale al quadrato del cambiamento per le misure lineari:
- aumenta di 100 volte con ogni salto che compio verso destra
- diminuisce di 100 volte con ogni salto che compio verso sinistra
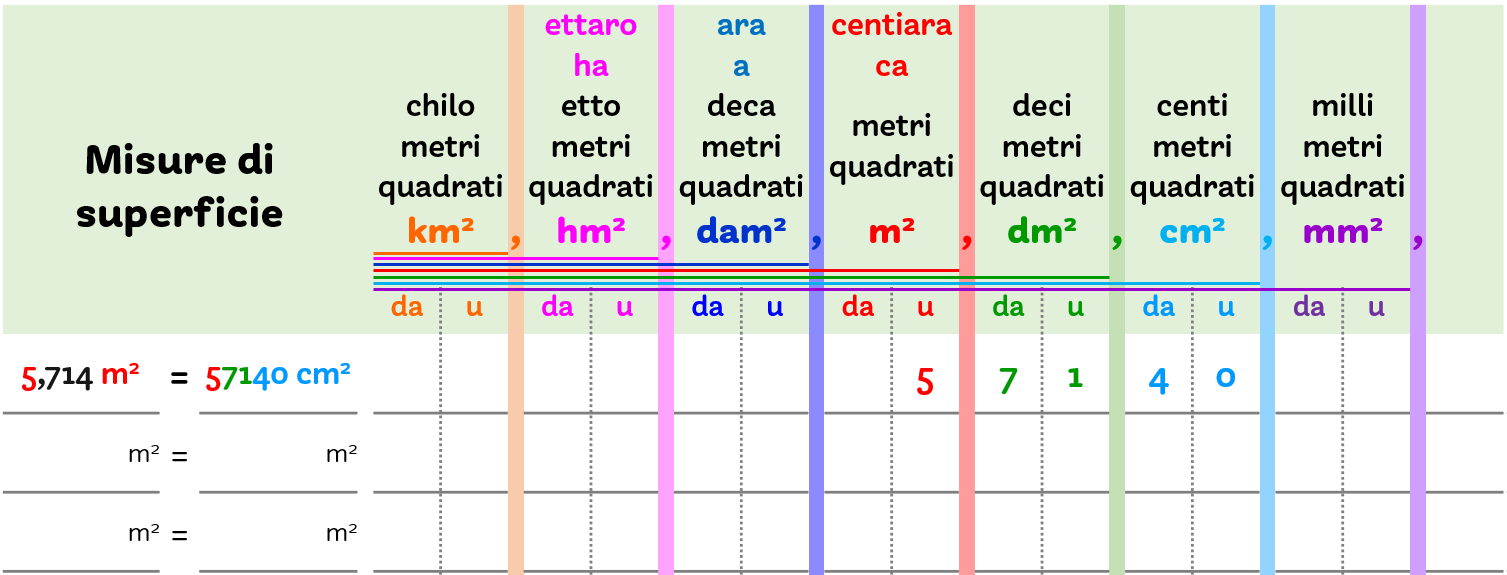
Individua la cifra delle unità e scrivila nella colonna dell’unità di misura indicata.
Per leggere il risultato in un’altra unità di misura usa la virgola che si trova alla sua destra.
Per leggere il risultato in un’altra unità di misura usa la virgola che si trova alla sua destra.
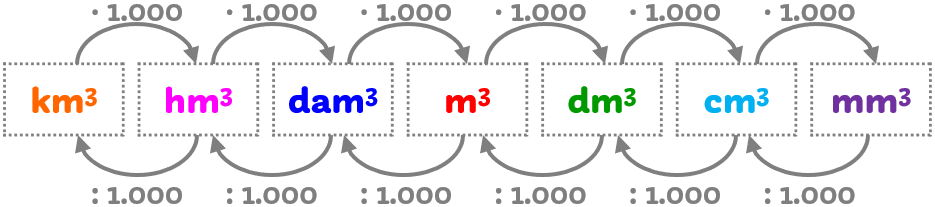
Le equivalenze tra le misure di volume
Il salto da un’unità di misura ad un’altra al suo fianco genera sempre un cambiamento che è uguale al cubo del cambiamento per le misure lineari:
- aumenta di 1.000 volte con ogni salto che compio verso destra
- diminuisce di 1.000 volte con ogni salto che compio verso sinistra
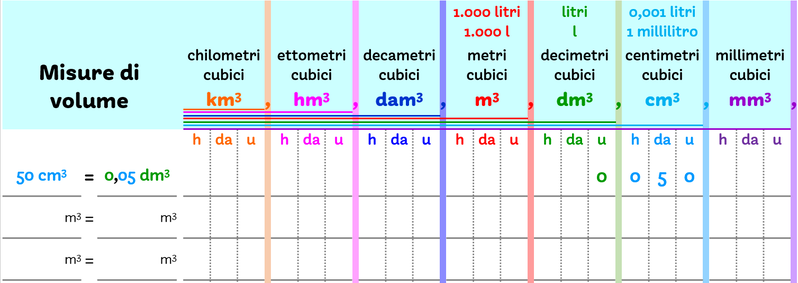
Individua la cifra delle unità e scrivila nella colonna dell’unità di misura indicata.
Per leggere il risultato in un’altra unità di misura usa la virgola che si trova alla sua destra.
Per leggere il risultato in un’altra unità di misura usa la virgola che si trova alla sua destra.
Le equivalenze tra misure di tempo
|
1 minuto = 60 secondi
|
x minuti = x : 60 secondi
|
|
1 ora = 60 minuti
1 ora = 60 · 60 secondi = 3.600 secondi |
x ore = x : 60 minuti
x ore = x : 3600 secondi |
|
1 giorno = 24 ore
1 giorno = 24 · 60 minuti = 1.440 minuti 1 giorno = 24 · 60 · 60 secondi = 86.400 secondi |
x giorni = x : 24 ore
x giorni = x : 1440 minuti x giorni = x : 86400 secondi |
|
1 anno = 365,25 giorni
1 anno = 365,25 · 24 ore = 8.766 ore 1 anno = 365,25 · 24 · 60 minuti = 525.960 minuti 1 anno = 365,25 · 24 · 60 · 60 secondi = 31.557.600 secondi |
x anni = x : 365,25 giorni
x anni = x : 8 766 ore x anni = x : 525 960 minuti x anni = x : 31 557 600 secondi |
|
secondo → s
|
minuto → min
|
ore → h
|
giorni → d
|
Scrivere una misura di tempo nella forma normale
Nella scrittura in forma normale:
- i secondi e i minuti sono minori di 60
- le ore sono minori di 24.
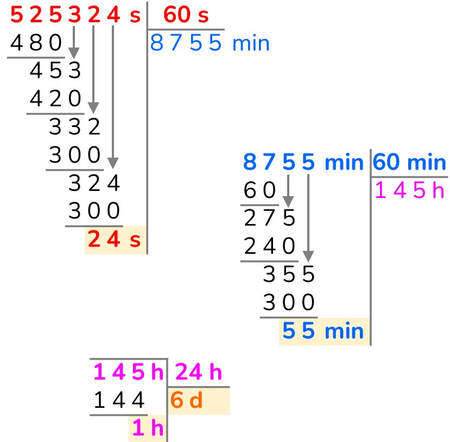
Scriviamo in forma normale la misura di 525324 s
- Quanti minuti in 525324 s? Dividiamo per la quantità di secondi contenuta in un minuto, cioè per 60. Il resto sarà la quantità di secondi da scrivere nella forma normale.
252324 s : 60 s = 8755 min + resto di 24 s. - Quante ore in 8755 min? Dividiamo per la quantità di minuti contenuta in un’ora, cioè per 60.
Il resto sarà la quantità di minuti da scrivere nella forma normale.
8755 min : 60 min = 145 h + resto di 55 min - Quanti giorni in 145 h? Dividiamo per la quantità delle ore contenuta in un giorno, cioè per 24.
Il resto sarà la quantità di ore da scrivere nella forma normale.
145 h : 24 h = 6 d + resto di 1 ora. - La misura di 525324 s corrisponde in forma normale a 6 d 1 h 55 min e 24 s
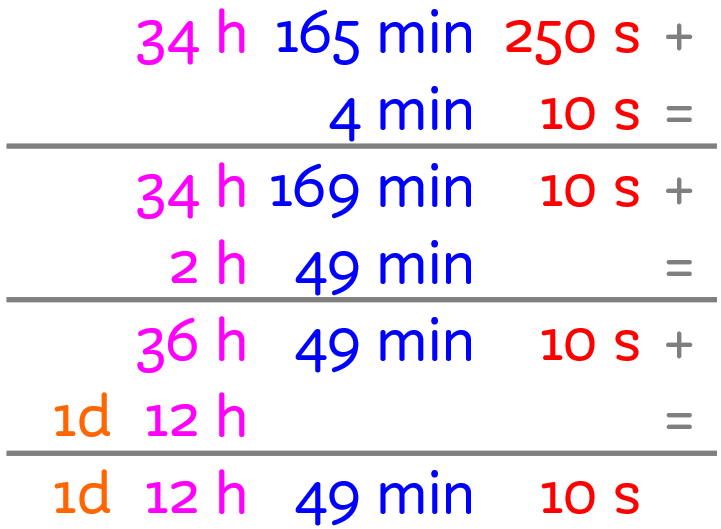
Scriviamo in forma normale 34 h 165 min e 250 s
|
I secondi superano 60 → 250 s : 60 s = 4 min con resto di 10 s.
Aggiungi i 4 min ai 169 già presenti, cancella i vecchi secondi e scrivi sotto 10s. 165 min + 4 min = 169 min I minuti superano 60 → 169 min : 60 min = 2 h e resto di 49 min. Aggiungi 2 h a quelle già presenti, cancella i vecchi minuti e metti 49 min.
34 h + 2 h = 36 h Le ore superano 24 → 36 h : 24 h = 1 d e 12 h. Aggiungi 1 alla colonna dei giorni, cancella le ore e metti 12h. |
Il volume e la capacità
Il volume è lo spazio occupato da un solido o da un liquido.
Si parla di capacità quando abbiamo a che fare con un contenitore, la sua capacità rappresenta il volume totale che può occupare la materia nello spazio tridimensionale che ha a disposizione.
Il volume di liquido o di solido che può occupare una sostanza in un certo contenitore prende il nome di capacità: la capacità della tua borraccia è di 5 cl, …
Si parla di capacità quando abbiamo a che fare con un contenitore, la sua capacità rappresenta il volume totale che può occupare la materia nello spazio tridimensionale che ha a disposizione.
Il volume di liquido o di solido che può occupare una sostanza in un certo contenitore prende il nome di capacità: la capacità della tua borraccia è di 5 cl, …
|
1 l = 1 dm³
|
1 l = 1000 cm³
|
1000 l = 1 m³
|
La velocità in m/sec e in Km/h
La velocità è espressa generalmente in metri al secondo o in chilometri orari.
Da chilometri orari a metri al secondo
Da metri al secondo a chilometri orari
La densità in g/dm³ e in Kg/m³
La densità è espressa generalmente in grammi per decimetro cubo o in chilogrammi per metro cubo.
Da chilogrammi per metro cubo a grammi per decimetro cubo
Da questo deriva che la densità espressa in kg/m3 o in g/dm3 hanno associati la stessa quantità numerica.
La misura della temperatura
L’unità di misura della temperatura usata nel Sistema Internazionale è il Kelvin.
In Italia si usa il centigrado, come pure Nel mondo sono utilizzate diverse unità di misura diverse dal Kelvin, le più comuni sono:
In Italia si usa il centigrado, come pure Nel mondo sono utilizzate diverse unità di misura diverse dal Kelvin, le più comuni sono:
- il grado centigrado:
0 °C = 273,15 K → la temperatura alla quale l’acqua passa dallo stato solido a quello liquido o viceversa
100 °C = 295,15 K → la temperatura alla quale l’acqua passa dallo stato liquido a quello di vapore o viceversa - il grado Fahrenheit:
da °C a °F → x °F = 1,8 · y °C + 32
da °F a °C → y °C = (x °F – 32) : 1,8
|
Contatore inserito il 28 novembre 2021
|
|