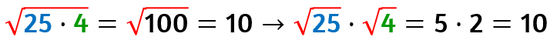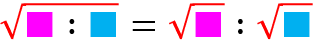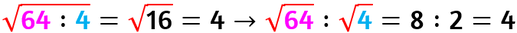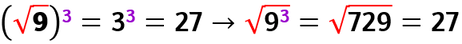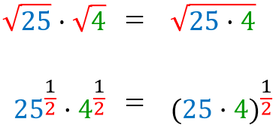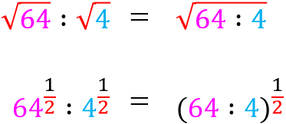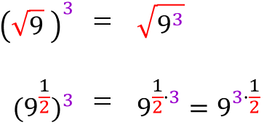L'OPERAZIONE DI RADICE

L’operazione di radice è una delle operazioni inverse dell’elevamento a potenza.
L’altra operazione inversa è il logaritmo.
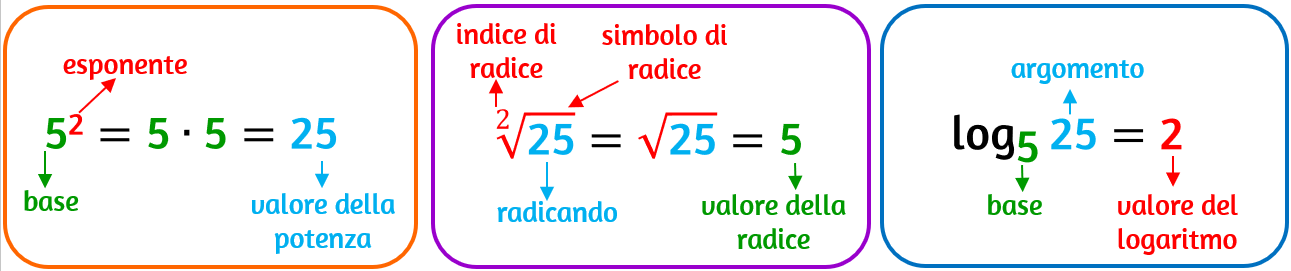
POTENZA
RADICE
LOGARITMO
Potenza: qual è quel ​numero che ottieni moltiplicando la
base​ per se stessa quante volte lo dice l’esponente?
Radice: qual è quel numero che moltiplicato per se stesso quante volte lo dice l’indice della radice mi dà il radicando?
Logaritmo: quale esponente devo dare alla base del logaritmo per ottenere l’argomento?

I numeri irrazionali

Quando si estrae la radice di un numero, la maggior parte delle volte otteniamo un numero decimale irrazionale, cioè un numero che non può essere scritto come frazione avente numeri interi sia al numeratore che al denominatore. 
Quando estraiamo un numero da una radice, otteniamo un numero naturale quando:
  • il radicando, di una radice quadrata, scomposto in fattori primi, è formato da potenze aventi tutte esponenti pari;
  • il radicando, di una radice cubica, scomposto in fattori primi, è formata da potenze aventi tutte come esponenti multipli di 3;
  • il radicando, di una radice quarta, scomposto in fattori primi, è formata da potenze aventi tutte come esponenti multipli di 4,
  • ... 
  • il radicando, di una radice n, scomposto in fattori primi, è formato da potenze aventi tutti come esponenti multipli di n. 
Quando estraiamo un numero decimale da una radice, otteniamo un numero razionale (decimale limitato o periodico) quando il radicando, espresso con la sua frazione generatrice, ridotta ai minimi termini, ha come numeratore e denominatore:
  • ​potenze aventi tutte esponenti pari se stiamo calcolando una radice quadrata;
  • potenze aventi tutte come esponenti multipli di 3, se stiamo calcolando una radice cubica;
  • potenze aventi tutte come esponenti multipli di 4, se stiamo calcolando una radice quarta;
  • ... 
  • potenze aventi tutti come esponenti multipli di n (un qualunque numero), se stiamo calcolando una radice ennesima (lo stesso numero n preso in esame prima). 
  • Dalla radice di un numero naturale puoi ottenere o un numero naturale o un numero irrazionale. 
  • Dalla radice di un numero decimale limitato puoi ottenere o un numero decimale limitato o un numero irrazionale.
  • Dalla radice di un numero decimale periodico puoi ottenere o un numero decimale periodico o un numero irrazionale.

Quadrati e cubi perfetti

Si chiama quadrato perfetto quel numero la cui radice quadrata è un numero naturale. 
La radice quadrata di un numero che non è un quadrato perfetto è un numero che dopo la virgola contiene un numero indefinito di cifre decimali e prende il nome di numero irrazionale.
Si chiama quadrato perfetto quel numero che si ottiene moltiplicando per sé stesso un numero  naturale:
  • 16 è un quadrato perfetto perché lo ottengo moltiplicando il 4 per sé stesso
    → 4 × 4 = 16
  • 144 è un quadrato perfetto perché lo ottengo moltiplicando il 12 per sé stesso
    → 12 × 12 = 144.
I quadrati perfetti, scomposti in fattori primi, sono formati da potenze aventi tutte esponente pari (multiplo di 2):
  • 16 = 2⁴
  • 144 = 2⁴ · 3²

​Si chiama cubo perfetto quel numero che si ottiene moltiplicando per sé stesso tre volte un numero naturale.
  • 8 è un cubo perfetto perché lo ottengo moltiplicando il 2 per sé stesso tre volte → 2×2×2=8
  • 125 è un cubo perfetto perché lo ottengo moltiplicando il 5 per sé stesso tre volte
    ​→ 5×5×5=125.
I cubi perfetti, scomposti in fattori primi, sono formati da potenze aventi tutte esponente multiplo di 3.

Proprietà delle radici

Come le potenza, anche le radici quadrate godono di alcune proprietà che se applicate opportunamente ci aiutano a semplificare i calcoli. 
Ricorda: le proprietà si applicano solo se le radici sono moltiplicate o divise.
RADICE DI UN PRODOTTO
La radice di un prodotto è uguale al prodotto delle radici dei singoli fattori.
RADICE DI UN QUOZIENTE
La radice di un quoziente è uguale al quoziente delle radici del dividendo e del divisore.
POTENZE DI RADICI
La potenza di una radice è uguale alla potenza del radicando della radice stessa. 
  • La radice quadrata equivale ad una potenza che ha come base il radicando e come esponente la frazione ½.
  • La radice terza equivale ad una potenza che ha come base il radicando e come esponente la frazione ⅓.    
  • La radice ennesima equivale ad una potenza che ha come base il radicando e come esponente la frazione unitaria con denominatore enne. 
Prodotto di radici e
radici di un prodotto
Quoziente di radici e
radice di un quoziente
Potenza di una radice e
radice di una potenza
Contatore inserito il 30 giugno 2021.