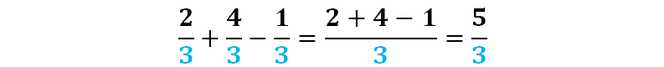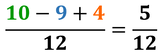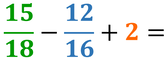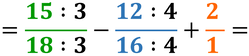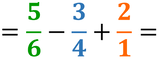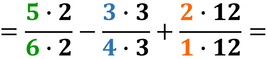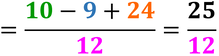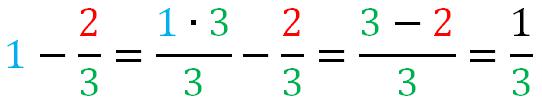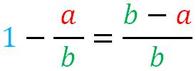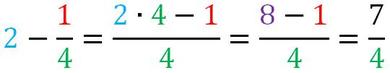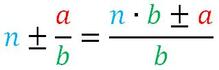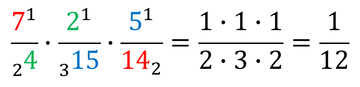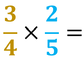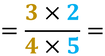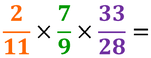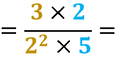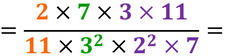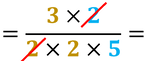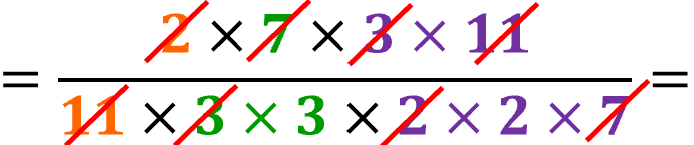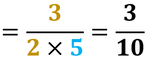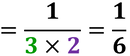LE OPERAZIONI DI ADDIZIONE E SOTTRAZIONE CON LE FRAZIONI
Somma e differenza di frazioni con lo stesso denominatore
|
La somma (differenza) di due frazioni aventi lo stesso denominatore è una frazione avente per denominatore lo stesso denominatore e per numeratore la somma (differenza) dei numeratori.
Se devo sommare e sottrarre frazioni che hanno lo stesso denominatore, dovrò: 1. riscrivo lo stesso denominatore 2. eseguo le operazioni tra i numeratori nell'ordine in cui si presentano 3. semplifico il risultato. |
|
Somma e differenza di frazioni con denominatore diverso
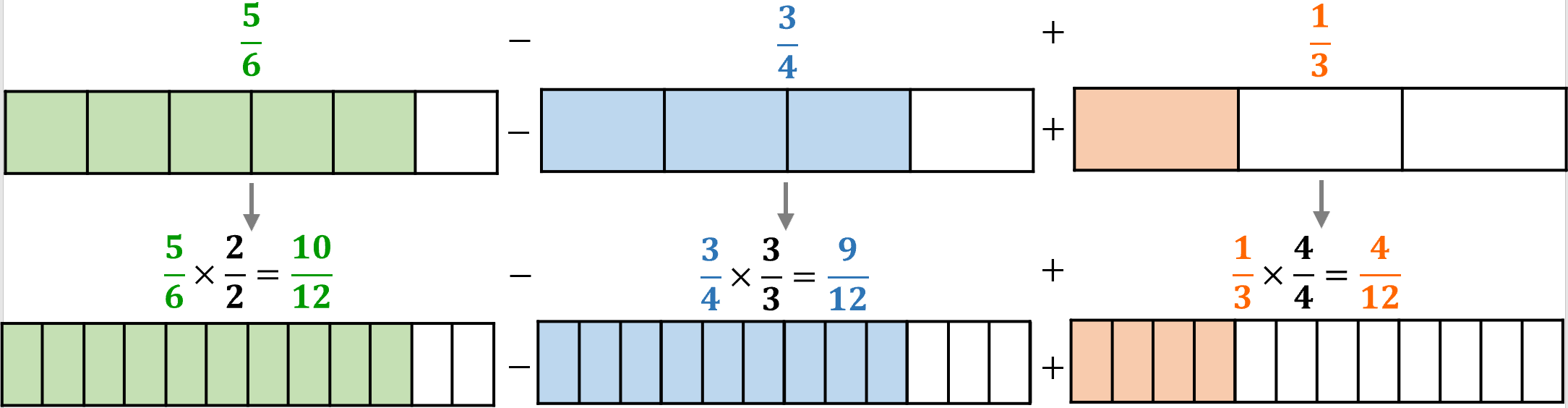
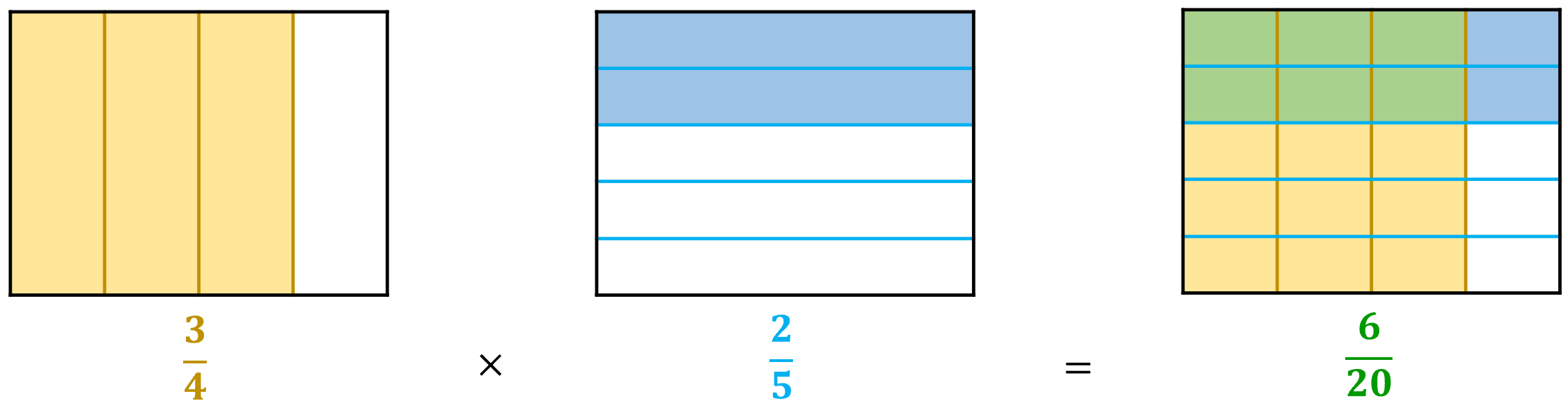
Per poter sommare o sottrarre (o anche per confrontare) due o più frazioni con diverso denominatore, è necessario trasformarle in frazioni equivalenti che avranno per denominatore il mcm dei denominatori, solo successivamente sarà possibile sommare o sottrarre i numeratori che avremo ottenuto.
Ora le frazioni hanno lo stesso denominatore, le parti in cui è stato diviso l’intero sono della stessa dimensione, per cui possiamo sia sommarle che sottrarle:
Ricorda: semplifica il risultato finale se è possibile.
Video spiegazione
Piccola espressione senza parentesi
|
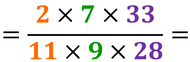
Semplifica tutte le frazioni riducibili e scrivi l’intero come frazione
Dividi numeratore e denominatore per una stessa quantità, e continua fino a quando la frazione è irriducibile, cioè non più semplificabile. Usa la tavola dei divisori e ricerca numeratore e denominatore per controllare il divisore comune a entrambi i numeri |
|
|
Trova il mcm tra tutti i denominatori (6, 4 e 1).
Prova a rispondere alla domanda: qual è il più piccolo numero comune alle tabelline del 6, del 4 e dell'1? Il 12 |
mcm (6, 4, 1) = 12
|
|
Trasformiamo ogni frazione in un'altra equivalente aventi tutte lo stesso denominatore.
Dividi il 12 per ogni denominatore e moltiplica il suo risultato sia per il numeratore che per il denominatore. |
|
|
Scriviamo tutto in un'unica frazione
Ora tutte le frazioni hanno lo stesso denominatore e possiamo lavorare solo sui numeratori. |
|
Ricorda di semplificare il risultato se è possibile.
ADDIZIONI PARTICOLARI
|
Secondo un antica leggenda, il dio egizio Horus perse un occhio in uno scontro, ma il dio della scienza riuscì con una magia a ricomporlo. Ma nonostante tutto ne mancava sempre una parte, sempre più piccola, maggiore era il numero delle parti… |
|
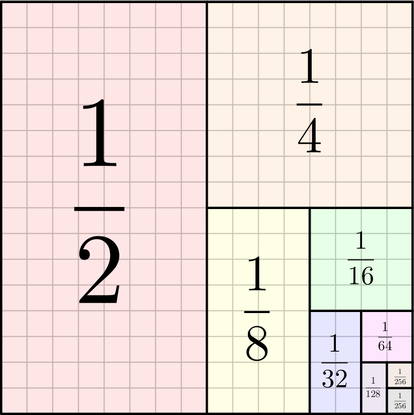
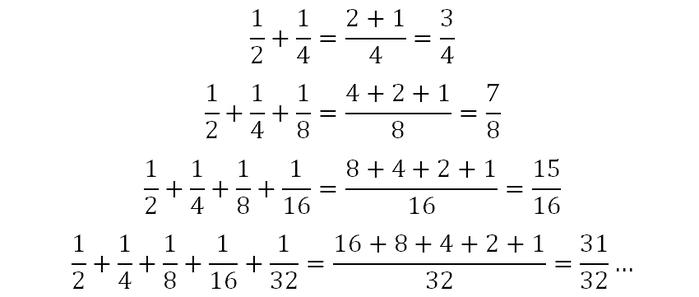
Guardate un po’ cosa succede sommando unità frazionarie di potenze di 2:
Come avrai già notato il risultato è formato da una frazione avente per denominatore il denominatore maggiore presente e per numeratore il consecutivo inferiore del numero del denominatore.
Sottrarre a 1 una frazione propria vuol dire calcolare la frazione complementare
Se sottraggo ad uno una frazione propria, il risultato è una frazione che avrà per denominatore lo stesso denominatore e per numeratore la differenza tra denominatore e numeratore.
La frazione complementare è quella frazione propria che sommata alla prima dà come risultato 1.
Le sue caratteristiche sono:
- ha lo stesso denominatore dell'altra frazione;
- ha come numeratore la differenza tra denominatore e numeratore.
Le sue caratteristiche sono:
- ha lo stesso denominatore dell'altra frazione;
- ha come numeratore la differenza tra denominatore e numeratore.
|
REGOLA |
|
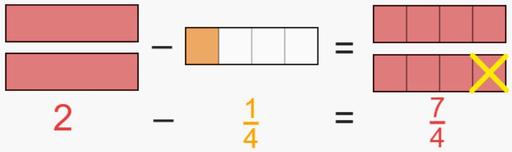
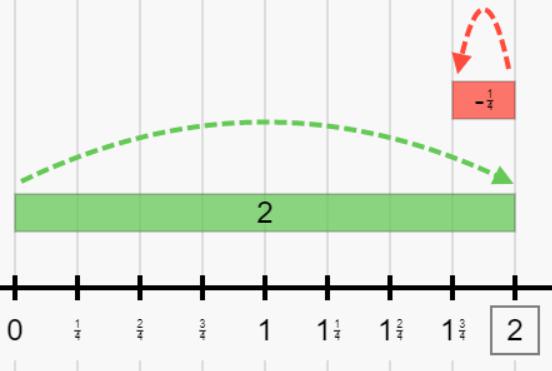
Sommare o sottrarre a un numero intero una frazione
Se sommo o sottraggo ad un numero intero una frazione, il risultato sarà uguale ad una frazione che avrà lo stesso denominatore e come numeratore la somma o la differenza tra tante volte il denominatore per il numero intero e il numeratore.
regola
Esercizi sulle frazioni dal sito: www.matematica.it
