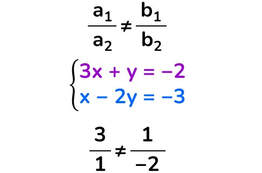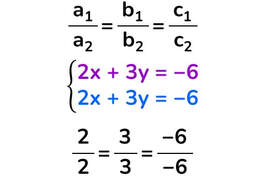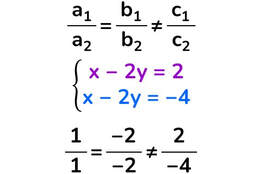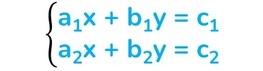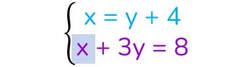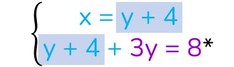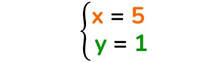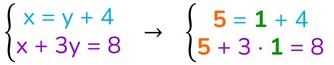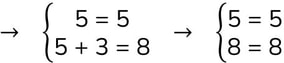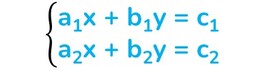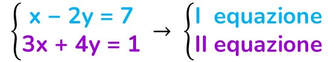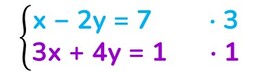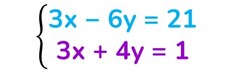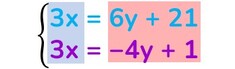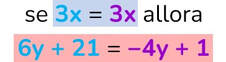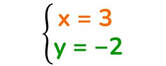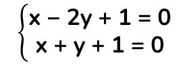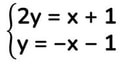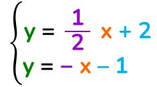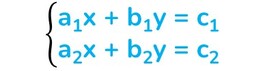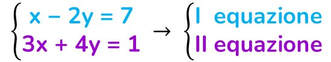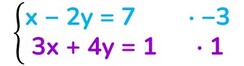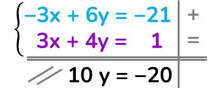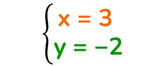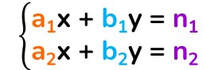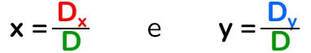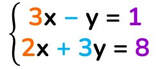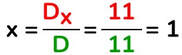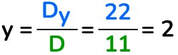I SISTEMI DI EQUAZIONE LINEARI

Quando si ha di fronte un’equazione lineare vuol dire avere a che fare con un polinomio nel quale compaiono solo lettere singole con esponente 1 (ogni monomio ha grado 1).

Un’equazione lineare in x e y rappresenta una retta in un piano cartesiano bidimensionale, un equazione lineare in x, y e z rappresenta una retta in un piano cartesiano tridimensionale.

Ogni equazione di primo grado è detta lineare perché rappresenta una retta nel piano cartesiano:

• se manca il termine letterale in y abbiamo una retta parallela all’asse y;
• se manca il termine letterale in x abbiamo una retta parallela all’asse x;
• se manca il termine noto abbiamo una retta che passa per l’origine degli assi;
• se abbiamo il termine in x, quello in y e il termine noto abbiamo una retta che non passa per l’origine e non è parallela agli assi cartesiani. 

Cosa vuol dire risolvere un sistema di equazioni?

Risolvere un sistema vuol dire trovare le coordinate del punto di intersezione tra le rette.
Ciò vuol dire che se sostituiamo alle incognite i valori trovati allora le equazioni sono vere.

Per poter risolvere un sistema di equazioni lineari possono essere usati diversi metodi, ma, ricorda, ciascuna equazione deve essere scritta in forma normale (nessun monomio simile presente nella singola equazione).

IMPORTANTE: un’equazione può essere trasformata in un’altra equivalente moltiplicando o dividendo tutti i termini dell’equazione per un numero diverso da zero.

Sistemi equivalenti → due sistemi si dicono equivalenti quando hanno lo stesso insieme di soluzioni.

​Le soluzioni di un sistema di equazioni

Per poter analizzare o risolvere un sistema di equazioni occorre sempre ridurlo alla forma normale (nella stessa equazione non devono comparire monomi simili e normalmente si tengono i termini letterali al primo membro e i termini noti al secondo membro):

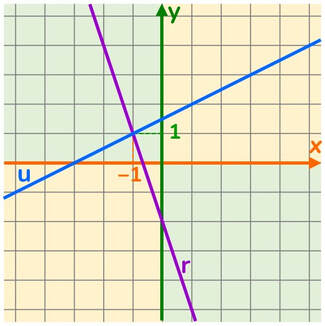
Sistema determinato

Quando esiste una coppia ordinata (x; y) di numeri appartenenti a ℝ che soddisfano entrambe le equazioni.

​Le due rette sono incidenti.

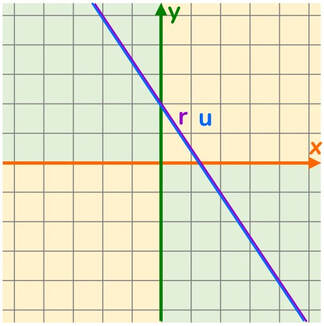
Sistema indeterminato

Qualunque punto appartenente alla prima equazione è anche appartenente alla seconda o viceversa. 

​Le due rette sono coincidenti. 

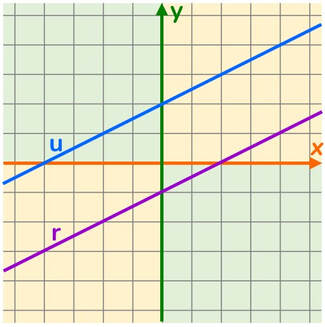
Sistema impossibile

Non esiste nessun punto appartenente alla prima equazione che sia anche un punto della seconda equazione. 

​Le due rette sono parallele.

---

Metodo di sostituzione

Riduci il sistema alla forma normale (non devono esserci monomi simili):

Per applicare il metodo di sostituzione dovrai:

1. isola un’incognita (la x o la y indifferentemente) in un’equazione a scelta;
2. sostituisci il valore dell’incognita appena trovato nell’altra equazione;
3. calcola il valore dell’incognita non sostituita;
4. sostituisci nell’altra equazione il valore trovato e calcola così il valore della seconda incognita.

LE SOLUZIONI COL METODO DI SOSTITUZIONE

Dopo aver sostituito un’incognita nell’altra, succede che se il sistema è:

determinato

​esistono solo due numeri appartenenti a ℝ che soddisfano entrambe le equazioni;

indeterminato

l’incognita sparisce ma al primo membro e al secondo membro compare lo stesso numero;

impossibile

​l’incognita sparisce e al primo membro c’è un numero diverso dal secondo membro. 

ESEMPIO DI SISTEMA RISOLTO COL METODO DI SOSTITUZIONE

Metti in evidenza una delle due incognite in una delle due equazioni (io ho scelto la x nella I equazione);

Sostituisci il valore trovato nell’altra equazione;

Risolvi la seconda equazione e trova il valore della y:

• lettere al I membro e termini noti al secondo membro (se sposti un termine da un membro all’altro devi cambiare segno);
• risolvi entrambi i membri;
• dividi entrambi i membri per il coefficiente della y.

* y + 3y = 8 − 4     →     4y = 4     →     y = 4/4     →     y = 1

Sostituisci alla y della I equazione il valore che hai appena trovato:

x = y + 4     →     x = 1 + 4     →      ​x = 5

Il risultato del sistema è:

Verifica del sistema appena risolto

1. Sostituisci alle incognite x e y di entrambe le equazioni i valori appena trovati;
2. risolvi il I e il II membro:

Poiché entrambe le equazioni sono diventate delle identità (il primo membro è uguale al secondo membro) allora le coordinate del punto di intersezione trovato è corretto.

---

Metodo del confronto

Riduci il sistema alla forma normale (non devono esserci monomi simili):

Per applicare il metodo del confronto dovrai:

1. controlla i coefficienti delle due incognite e se diversi moltiplica tutti i termini della prima equazione e/o della seconda equazione per uno stesso numero di modo da rendere la stessa incognita con lo stesso coefficiente in entrambe le equazioni;
2. isola al primo membro le due incognite uguali in entrambe le equazioni;
3. scrivi un’equazione di primo grado data dall’uguaglianza dei rispettivi secondi membri;
4. sostituisci in una delle due equazioni originali il valore trovato della prima incognita per trovare l’altra.

​Le soluzioni col metodo del confronto

Dopo aver isolato la stessa incognita in entrambe le equazioni, succede che se il sistema è:

determinato

i coefficienti dell’incognita non isolata nei secondi membri sono diversi;

indeterminato

i primi membri sono identici e anche i secondi membri sono identici;

impossibile

​le incognite al secondo membro hanno lo stesso coefficiente ma i termini noti sono diversi. 

Esempio di sistema risolto col metodo del confronto

Coefficienti della x in entrambe le equazioni: 1 e 3. → mcm (1; 3) = 3

Trasforma la prima equazione in un’altra equivalente moltiplicando tutti i suoi termini per 3;

lascia invariati tutti i termini della seconda equazione;

L’incognita x è identica in entrambe le equazioni.
Isola l’incognita x in entrambe le equazioni.

Se i primi membri sono tra loro uguali, allora anche i secondi membri  sono equivalenti.

Risolvi l’equazione in primo grado.

6y + 4y = − 21 + 1
10y = −20
y = −20/10
y = −2

Sostituisci in una delle due equazioni il valore della y appena trovato (io ho scelto la prima equazione che mi permette di trovare direttamente il valore della x):

x − 2y = 7
x = 2y + 7 = 2·(−2) + 7 =
​= −4 + 7 = 3
​x = 3

Il risultato del sistema è:

---

Metodo grafico

Si chiama metodo grafico quel modo nel quale:

1. scrivi nella forma esplicita, y = mx + q, l’equazione di ciascuna delle due rette;
2. compili una tabella di valori attribuendo alla x un valore a scelta, positivo o negativo, generalmente multiplo del denominatore del coefficiente della x, qualora fosse una frazione;
3. calcola per ciascun valore attribuito alla x quello corrispondente della y;
4. inserisci nel piano cartesiano i punti corrispondenti alle coppie di valori x e y;
5. unisci i punti e disegna la retta;
6. individua il punto di intersezione tra le due rette e determina le sue coordinate.

Le soluzioni col metodo grafico

Dopo aver scritto l’equazione delle due rette nella forma esplicita:

succede che se il sistema è:

determinato

​m₁ ≠ m₂
le due rette sono incidenti; 

indeterminato

m₁ = m₂ e q₁ = q₂
le due rette sono coincidenti;

impossibile

m₁ = m₂ e q₁ ≠ q₂
le due rette sono parallele.

Esempio di sistema risolto col metodo grafico

Scrivi le equazioni delle due rette nella forma esplicita y = mx + q:

​isola la y in entrambe le equazioni

dividi tutti i termini della prima equazione per il coeff. della y

costruiamo due tabelle di valori per poter calcolare le coordinate di alcuni punti delle due rette:

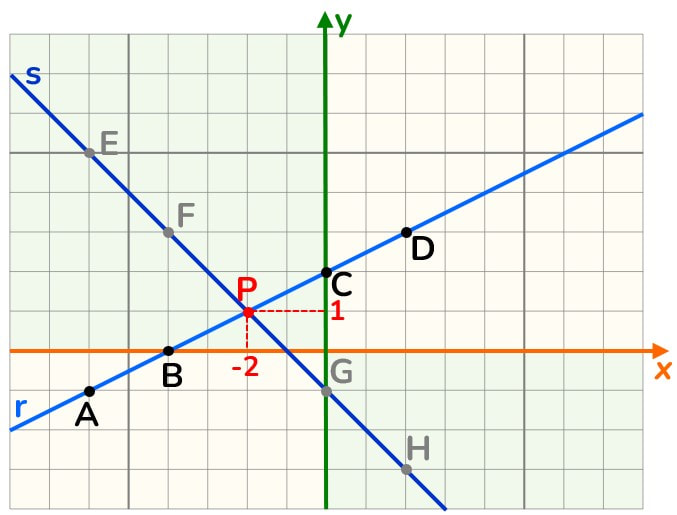
Metti i punti della retta r sul piano cartesiano individuando prima la coordinata x e poi vai verso l’alto o verso il basso per raggiungere la coordinata y. Traccia la retta usando il tuo righello.

Metti i punti della retta s sul piano cartesiano, procedendo come hai già fatto prima per la retta r.

Il punto di intersezione tra le rette r e s è il punto P che ha ascissa −2 e ordinata 1.

r ⋂ s = P

---

Metodo di riduzione

Riduci il sistema alla forma normale (non devono esserci monomi simili):

Per applicare il metodo di riduzione dovrai:

1. controllare i coefficienti delle due incognite, farai in modo di farli diventare opposti moltiplicando tutti i termini della prima equazione e/o della seconda equazione per uno stesso numero;
2. somma la prima equazione alla seconda equazione in colonna;
3. calcola il valore dell’incognita rimasta;
4. sostituisci in una delle due equazioni originali il valore trovato della prima incognita per trovare l’altra.

Le soluzioni col metodo di riduzione

Dopo aver fatto trasformato entrambe le equazioni (o solo una) di modo da avere due incognite opposte, succede che se il sistema è:

determinato

il coeff. dell’altra incognita non è opposto;

indeterminato

il coeff. dell’altra incognita è opposto come è opposto anche il termine noto;

impossibile

il coeff. dell’altra incognita è opposto ma il termine noto non è opposto. 

Esempio di sistema risolto col metodo del confronto

Vorrei eliminare i termini in x:
- moltiplicherò per −3 tutti i termini della prima equazione;
- lascio invariati tutti i termini della seconda equazione;

Somma membro a membro i termini con la x, i termini con la y e i termini noti;

Calcola il valore della y dividendo entrambi i membri dell’equazione somma:

y = −20/10
y = −2 

Sostituisci in una delle due equazioni il valore della y appena trovato (io ho scelto la prima equazione che mi permette di trovare direttamente il valore della x):

x − 2y = 7
x = 2y + 7 = 2·(−2) + 7 =
​= −4 + 7 = 3
​x = 3

Il risultato del sistema è:

---

Metodo di Cramer

Riduci il sistema alla forma normale (non devono esserci monomi simili):

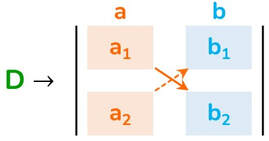
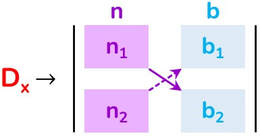
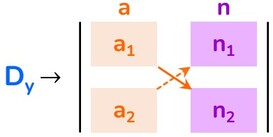
Costruiamo tre tabelle formate da 2 colonne e da 2 righe che chiamiamo matrice quadrata. In ogni colonna dovranno comparire i coefficienti della x, i coefficienti della y o i termini noti. ​

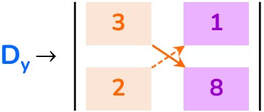
Si chiama determinante D il numero dato dalla differenza tra il prodotto dei numeri della diagonale con corpo in continuo e il prodotto dei numeri della diagonale con corpo tratteggiato. ​

D = a₁ · b₂ − a₂ · b₁​

Dx = n₁ · b₂ − n₂ · b₁

Dy = a₁ · n₂ − a₂ · n₁ ​

I valori delle incognite x e y sono dati dai seguenti rapporti: ​

Le soluzioni col metodo di Cramer

Scrivi il sistema in forma normale e calcola i tre determinanti, succede che il sistema è:

determinato

​Quando D ≠ 0.

indeterminato

Quando D = Dx = Dy = 0.

impossibile

Quando D = 0 ma Dx ≠ 0 e Dy ≠ 0.

Esempio di sistema risolto col metodo di Cramer

Dopo aver scritto il sistema in forma normale, compila le tre matrici e calcola i tre determinanti:

Con la prima matrice calcoli il determinante D che avrà nella prima colonna i coefficienti della x mentre nella seconda i coefficienti della y.

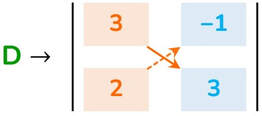
​Il valore del determinante D è così calcolato:

D = a₁ · b₂ − a₂ · b₁ = 3 · 3 − 2 · (-1) = 9 + 2 = 11

Con la seconda matrice calcoli il determinante Dx che sarà simile a quella precedente ma avrà i termini noti al posto dei coeff. della x.

​Il valore del determinante Dx è così calcolato:

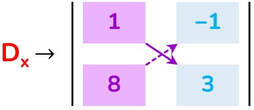
Dx = n₁ · b₂ − n₂ · b₁ = 1 · 3 − 8 · (-1) = 3 + 8 = 11

Ora puoi calcolare il valore dell’incognita x: ​

Con la terza matrice calcoli il determinante Dy che sarà simile alla prima matrice ma ci saranno i termini noti al posto dei coeff. della y. 

​Il valore del determinante Dy è così calcolato:​

Dy = a₁ · n₂ − a₂ · n₁ = 3 · 8 − 2 · 1 = 24 – 2 = 22

Ora puoi calcolare il valore dell’incognita y:

Pagina creata il 29 dicembre 2022