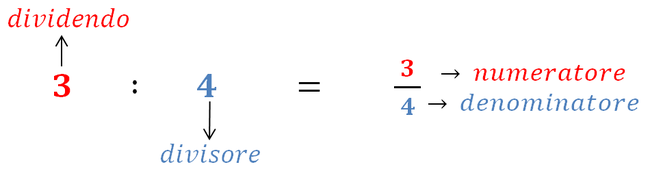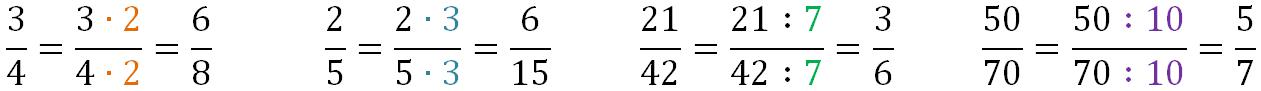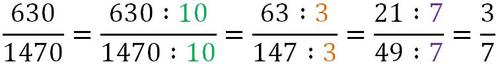LE FRAZIONI, DEFINIZIONE E CARATTERISTICHE
Nel linguaggio comune, si chiama frazione una parte dell'intero, del totale. La frazione di una città è una parte della città distaccata dal centro abitato principale, ma che, come popolazione partecipa al numero totale di abitanti.
|
Definizione - Si chiama frazione quell’operazione che divide un intero in parti uguali e ne considera almeno una parte dei suoi pezzi.
Una frazione è un modo diverso di vedere una divisione:
|
|
L'unità frazionaria
Un'unità frazionaria è una frazione che ha come numeratore il numero 1, rappresenta, cioè, una delle parti uguali in cui è stato diviso l’intero.
CLASSIFICAZIONE DELLE FRAZIONI
In base alla definizione di frazione “dividere un intero in parti uguali e prenderne un certo numero di essi...”, scaturisce la possibilità di avere solo due tipi di frazione, quelle che avranno numeratore uguale o minore al denominatore. Nella realtà è possibile avere un altro tipo di frazione, detta impropria, proprio perché non rispecchia la definizione di frazione, nella quale il numeratore è maggiore del denominatore ed il suo valore è maggiore dell'intero. Eccovi uno schema nel quale richiamare tutti i concetti ora visti:
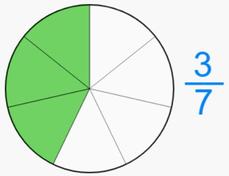
Frazioni proprie
Sono proprio delle frazioni, cioè una parte dell'intero.
Il loro valore è sempre più piccolo di 1.
Il loro valore è sempre più piccolo di 1.
Il sopra (numeratore) è più piccolo del sotto (denominatore).
L'intero è stato diviso in 7 parti uguali e ne abbiamo colorato 3 di queste parti.
|
L'intero è stato diviso in 8 parti uguali e ne abbiamo preso 7 di queste parti.
|
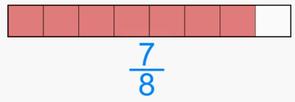
Frazioni improprie
Sono più dell'intero, pertanto sono "anomale", il termine frazione è usato impropriamente.
Il loro valore è sempre maggiore di 1.
Il loro valore è sempre maggiore di 1.
Il sopra (numeratore) è più grande del sotto (denominatore).
Dovremmo dividere l'intero in 5 parti uguali e poi prendere 7 di queste parti. Ma, non è possibile, sono necessari 2 interi: uno occorre completo e del secondo ne occorrono 2 delle sue 5 parti.
|
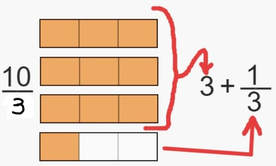
Dovremmo dividere l'intero in 3 parti uguali e poi prendere 10 di queste parti. Ma, non è possibile, sono necessari 4 interi: 3 occorrono completi e del quarto ne occorre solo una delle sue 3 parti.
|
Frazioni apparenti
Sembrano frazioni ma nella realtà non lo sono. Il loro valore è un numero intero (1, 2, 3, ...).
Generalmente sono frazioni improprie, tranne quando il numeratore è uguale al denominatore.
Generalmente sono frazioni improprie, tranne quando il numeratore è uguale al denominatore.
Il sopra (numeratore) è divisibile per il numero sotto (denominatore).
Nelle frazioni apparenti ci viene richiesto di dividere l'intero in una quantità di parti che è esattamente divisore della quantità che dovrei prendere.
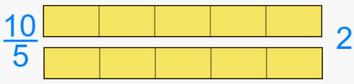
Divido l'intero in 5 parti uguali. Ma, per prenderne 10 mi occorrono due interi completi. Non avanza neanche una parte.
Ciò che sembrava una frazione era nella realtà un numero intero. |
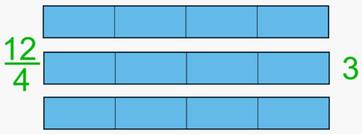
Divido l'intero in 4 parti uguali. Ma, per prenderne 12 mi occorrono 3 interi completi.
Non avanza neanche una parte. |
Frazioni e modelli
(clicca sul link sotto per comprendere meglio il concetto di frazione):
https://www.nctm.org/Classroom-Resources/Illuminations/Interactives/Fraction-Models/
(clicca sul link sotto per comprendere meglio il concetto di frazione):
https://www.nctm.org/Classroom-Resources/Illuminations/Interactives/Fraction-Models/
Trasformare una frazione impropria in un numero misto
Si dice numero misto un’espressione formata da un numero intero e da una frazione propria.
Nei fogli di calcolo come Excel, come pure nelle calcolatrici scientifiche, quando il formato della cella è impostato come frazione, qualora si scriva una frazione impropria essa restituisce un numero intero con al suo fianco una frazione propria, il segno sottinteso in questo caso è quello di addizione.
Per trasformare una frazione impropria in un numero misto:
- numero intero: è quante volte il denominatore sta nel numeratore;
- frazione: il resto della divisione fatta per ottenere il numero intero è il numeratore, il denominatore è lo stesso che era presente nella frazione impropria.
Nei fogli di calcolo come Excel, come pure nelle calcolatrici scientifiche, quando il formato della cella è impostato come frazione, qualora si scriva una frazione impropria essa restituisce un numero intero con al suo fianco una frazione propria, il segno sottinteso in questo caso è quello di addizione.
Per trasformare una frazione impropria in un numero misto:
- numero intero: è quante volte il denominatore sta nel numeratore;
- frazione: il resto della divisione fatta per ottenere il numero intero è il numeratore, il denominatore è lo stesso che era presente nella frazione impropria.
Esempio
Vogliamo trasformare la frazione 9/4 in un numero misto.
Domanda: quante volte il 4 è contenuto nel 9?
Risposta: 2 volte.
2 è il numero intero che stavamo cercando.
Domanda: quante parti mi avanzano se tolgo le due parti intere?
Risposta: 1 parte.
1 è il numeratore della frazione propria, il denominatore rimarrà il 4.
Vogliamo trasformare la frazione 9/4 in un numero misto.
Domanda: quante volte il 4 è contenuto nel 9?
Risposta: 2 volte.
2 è il numero intero che stavamo cercando.
Domanda: quante parti mi avanzano se tolgo le due parti intere?
Risposta: 1 parte.
1 è il numeratore della frazione propria, il denominatore rimarrà il 4.
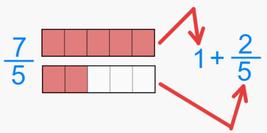
Nell'immagine sopra ho rappresentato la frazione 9/4.
Si può notare che per poterla rappresentare ho avuto bisogno di tre oggetti, che ho diviso in 4 parti (il denominatore è 4!).
Dall'immagine si evince che la frazione 9/4 è formata da due parti intere e dalla frazione 1/4.
Si può notare che per poterla rappresentare ho avuto bisogno di tre oggetti, che ho diviso in 4 parti (il denominatore è 4!).
Dall'immagine si evince che la frazione 9/4 è formata da due parti intere e dalla frazione 1/4.
Le frazioni equivalenti
Due o più frazioni si dicono equivalenti quando indicano la stessa quantità.
Come passare da una frazione ad un’altra ad essa equivalente Per passare da una frazione ad un’altra equivalente basta applicare la proprietà invariantiva delle divisioni (essendo la frazione una divisione vista in modo diverso), detta anche proprietà fondamentale delle frazioni, che dice:
Come passare da una frazione ad un’altra ad essa equivalente Per passare da una frazione ad un’altra equivalente basta applicare la proprietà invariantiva delle divisioni (essendo la frazione una divisione vista in modo diverso), detta anche proprietà fondamentale delle frazioni, che dice:
Proprietà fondamentale o invariantiva: se moltiplico o divido, per uno stessa quantità diversa da zero, sia il numeratore che il denominatore di una frazione, si ottiene una frazione equivalente a quella data.
Semplificare una frazione = ridurre una frazione ai minimi termini
Definizione - Una frazione si dice irriducibile o ridotta ai minimi termini (non semplificabile) quando il numeratore e il denominatore sono numeri primi fra loro.
Due numeri sono primi fra loro quando:
Due numeri sono primi fra loro quando:
- i due numeri non hanno nessun divisore in comune;
- i due numeri sono consecutivi (ad esempio, 152 e 153);
- i due numeri sono dispari consecutivi (ad esempio 545 e 547);
- il più grande dei due numeri è un numero primo.
Definizione - Una frazione è riducibile (si può semplificare) quando numeratore e denominatore hanno divisori comuni (possono essere divisi entrambi per una stessa quantità).
Per ridurre una frazione ai minimi termini:
Per ridurre una frazione ai minimi termini:
- si dividono numeratore e denominatore per il loro MCD oppure
- si dividono numeratore e denominatore per una stessa quantità e si continua così sino a quando non sarà più possibile
