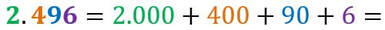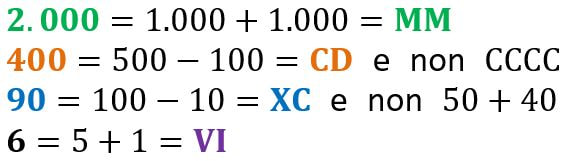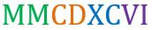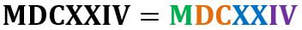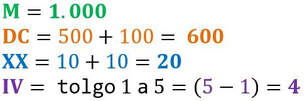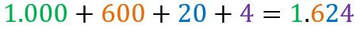Sistema di numerazione romana

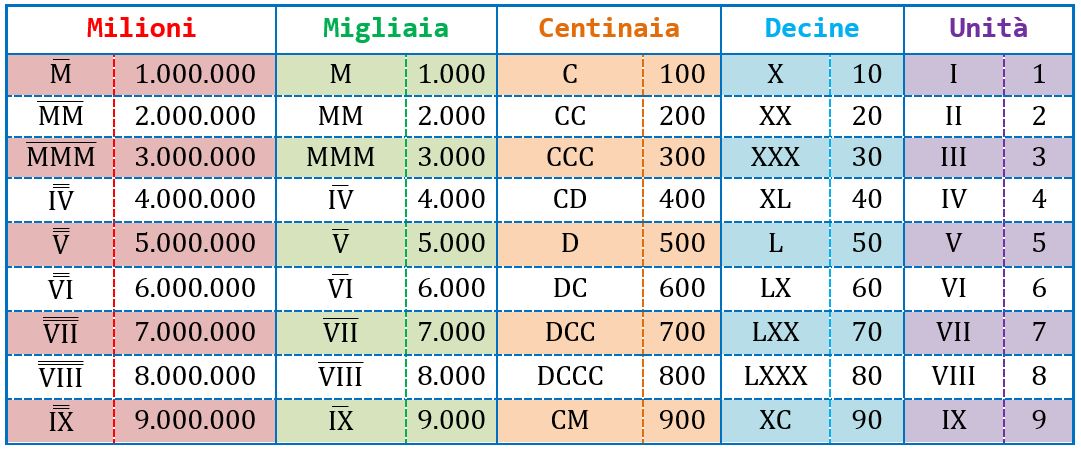
Il sistema di numerazione romano è un sistema molto antico che usa in totale 7 simboli I, V, X, L, C, D e M. 

In questo sistema, detto additivo-sottrattivo (si usano solo l’addizione e la sottrazione) esistono delle regole:
Regole:

• I simboli con valore minore vanno sempre a destra, quelli col valore maggiore vanno a sinistra;
• quando un simbolo con valore basso anticipa un simbolo con valore più alto, vuol dire che deve essere sottratto (IX si può leggere come “tolgo 1 a 10”);
• i simboli I, X, C e M possono essere aggiunti ma non possono comparire più di tre volte consecutivamente;
• i simboli I, X e C possono essere sottratti, ma non possono essere tolti per più di una volta:
  • cioè posso togliere I a X per formare il numero 9, IX, ma non posso togliere I a C per formare il 99;
• i simboli V, L e D
  • possono essere SOLO aggiunti e MAI sottratti;
  • non possono comparire più di una volta;
• non si può mai togliere un valore minore di dieci volte;
• una linea orizzontale sopra uno o più simboli ne aumenta il valore di  (mille) volte;
• due linee orizzontali sopra uno o più simboli ne aumenta il valore di  (un milione) di volte.

• con i simboli I, V, X, L, C, D e M è possibile scrivere tutti i numeri da 1 a 3.999, per i numeri più grandi è stato poi introdotta una linea sopra il simbolo che indica che quella cifra va moltiplicata per mille, mentre due linee sopra il simbolo indicano che la cifra sotto va moltiplicata per un milione.

---

---

Trasformare un numero decimale in numero romano

​1. Scomporre le cifre che compongono il
​   numero, secondo il loro valore

2. Tra i simboli vedo se posso ottenere la
   scomposizione abbinando somme e/o
​   differenze

3. Metto insieme i simboli

    

---

Trasformare un numero romano in decimale

1. Scomporre le cifre che compongono il 
   numero, secondo il loro valore;

   

2. Traduco i simboli nei loro valori:

• simbolo grande, simbolo piccolo, si somma
• simbolo piccolo, simbolo grande si toglie al grande il piccolo

3. Ricompongo il numero sommando i valori.

---

Sapete il perché dei diversi simboli?

• I sta per un dito, o comunque un bastoncino;
• V sta per una mano aperta;
• X sta per due mani aperte messe una sopra l’altra;
• se siete poi curiosi di conoscere il perché degli altri simboli vi suggerisco di dare una lettura a quanto dice questo sito internet: http://storiaenigmi.blogspot.com/2012/09/i-numeri-romani.html?m=1.

Il numero 5 = V

Il numero 10 = X

---

Dove si usano oggi i numeri romani:

​Oggi i numeri romani si usano:

• per indicare il secolo di appartenenza di un determinato avvenimento (siamo nel XXI secolo, vuol dire che apparteniamo agli anni compresi tra il 2000 e il 2100);
• come numeri ordinali al posto dei numeri arabi con il simbolo ° posto alla fine. Li vediamo ad esempio a Cagliari nei cartelli stradali per indicare la settimana di pulizia mensile (III lunedì del mese = 3° lunedì del mese);
  RICORDA: 1° = I, 2° = II, …, 43° = XLIII, …
  pertanto i numeri ordinali se scritti come numeri romani non hanno MAI °, invece se scritti con i numeri arabi devono sempre avere ° alla fine del numero.

---