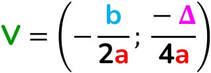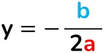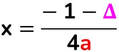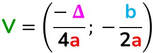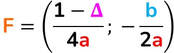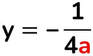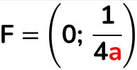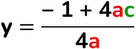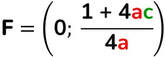LA PARABOLA

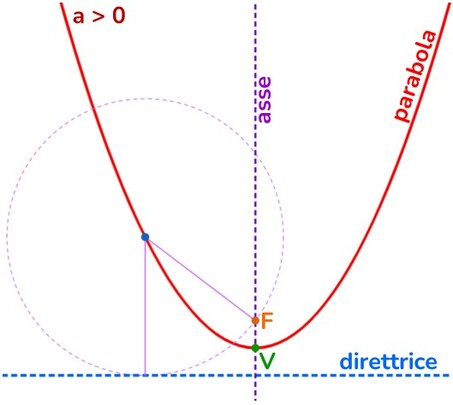
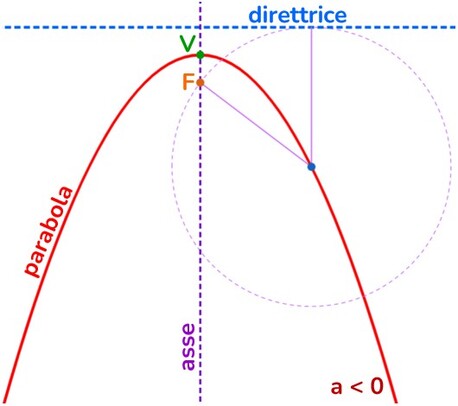
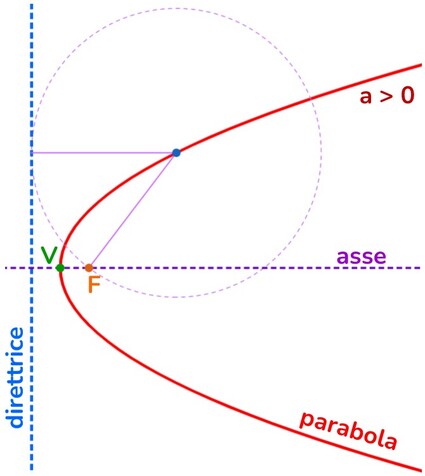
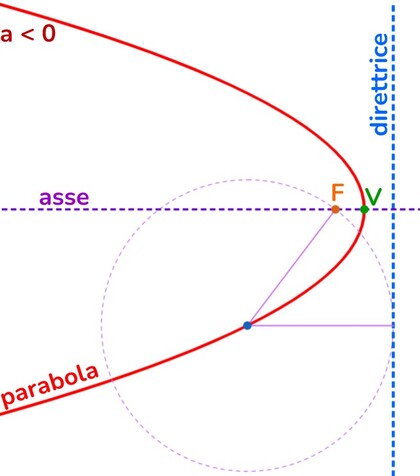
Si chiama parabola quella curva ottenuta dai punti che hanno stessa distanza da una retta ( detta direttrice) e da un punto fisso (che chiameremo fuoco).

Nella parabola possiamo riconoscere:

• Asse → ciò che divide la parabola in due parti simmetriche
• Vertice → è il punto di intersezione tra l’asse e la parabola. Se la parabola ha asse verticale il vertice potrà rappresentare il punto di minimo (se ha concavità rivolta verso l’alto) o di massimo (se la concavità è rivolta verso l’alto.
• Direttrice → retta perpendicolare all’asse che si trova da parte opposta del fuoco rispetto al fuoco e che ha stessa distanza FV.

Quante parabole possono essere rappresentate?

Le parabole che possono essere rappresentate sono infinite, ma nei libri scolastici della scuola superiore si discutono solo i casi nei quali l'asse di simmetria è parallelo ad uno dei due assi (x oppure y).

​Parabola con asse perpendicolare all’asse x (che vuole anche dire parallelo all'asse delle y o delle ordinate)

​L’equazione generale di una parabola con asse parallelo alle ordinate è una funzione di secondo grado la cui formula è:

y = ax² + bx + c

​Ricorda: Δ = b² – 4ac

Equazione dell’asse

Equazione della direttrice

Coordinate del vertice

Coordinate del fuoco

​Parabola con asse perpendicolare all’asse y (che vuole anche dire parallelo all'asse delle x o delle ascisse)

​L’equazione generale di una parabola con asse parallelo alle ascisse è una funzione di secondo grado la cui formula è:

x = ay² + by + c

Le formule sono "quasi" le stesse viste per la parabola con asse alle ordinate, ma con tutti i valori di x e y scambiati di posto.

Equazione dell’asse

Equazione della direttrice

Coordinate del vertice

Coordinate del fuoco

I coefficienti a, b e c nella parabola con asse parallelo alle ordinate

I coefficienti dell’equazione esplicita di una parabola, oltre a fornici delle informazioni sulle coordinate del vertice, del fuoco, della direttrice e dell’asse, ci danno delle informazioni importanti sulla sua apertura, sul verso della concavità, sulla posizione dell’asse e sui punti di intersezione con l’asse delle ordinate (asse y). ​

Nell'immagine modifica i valori di a, b e c e vedrai come la parabola cambierà.

Il coefficiente a è anche definito apertura, questo perché ci fornisce delle indicazioni sulle caratteristiche generali della parabola (forma e orientamento):

• più il valore del coefficiente a si avvicina allo 0, sia dalla parte positiva (da +∞ a 0) che dalla parte negativa (da da −∞ a 0), maggiore è l’apertura della parabola; conseguentemente, più a aumenta, in valore assoluto, più stretta sarà la parabola;
• se il coefficiente a è positivo → la parabola è rivolta verso l’alto (si avrà così un punto di minimo che corrisponde al vertice della parabola, al di sotto del quale la funzione non esiste);
  se il coefficiente a è negativo → la parabola è rivolta verso il basso (si avrà così un punto di massimo che corrisponde al vertice della parabola, al di sopra del quale la funzione non esiste). 

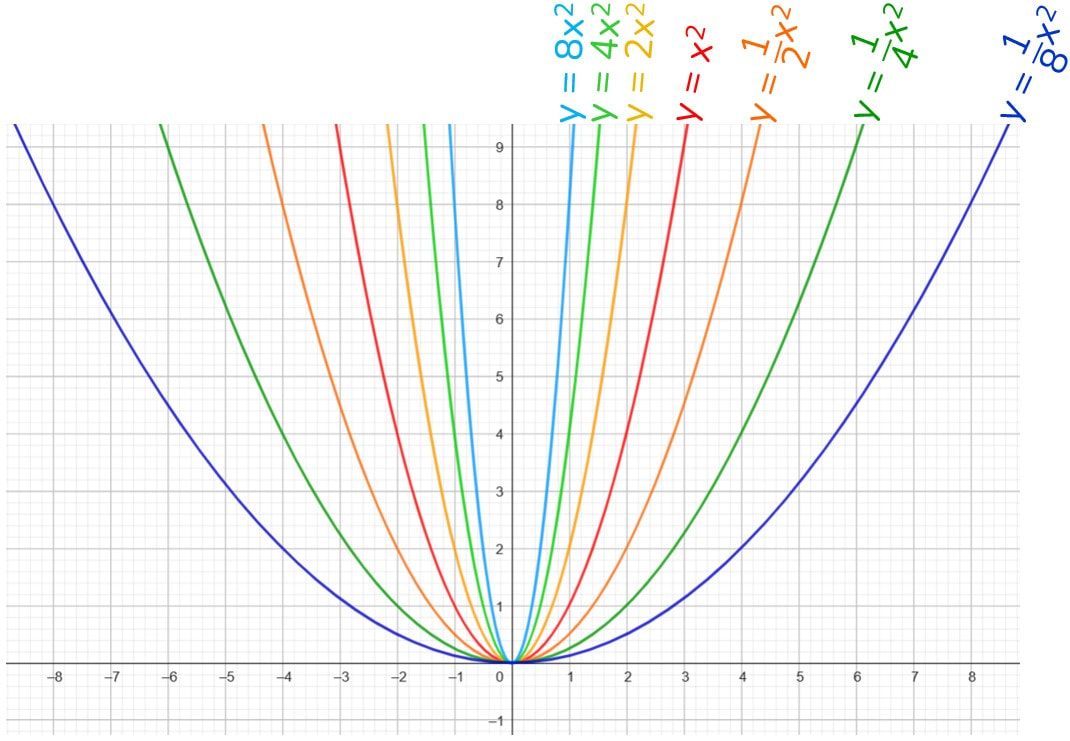
Coefficiente a positivo si traduce nell’avere la concavità rivolta verso l’alto.
La parabola di equazione y = x² è quella in rosso e la prendiamo come riferimento.
Tutte le parabole con coefficiente maggiore di 1 risultano essere meno aperte.
Tutte le parabole con coefficiente compreso tra 0 e 1 risultano essere molto più aperte. ​

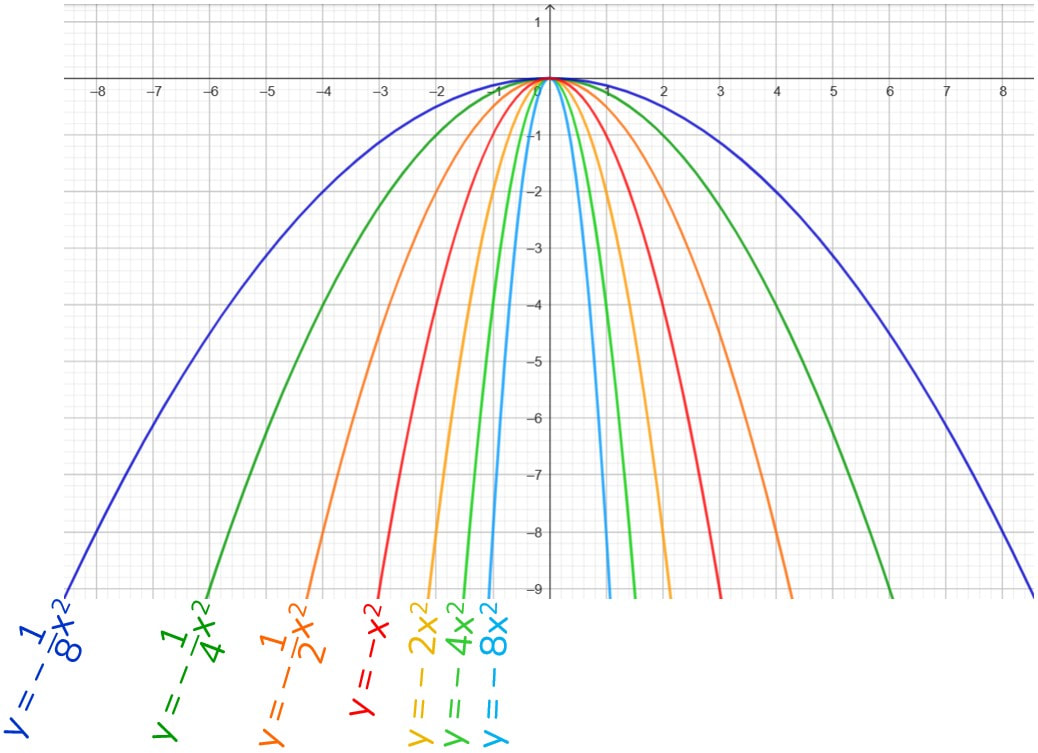
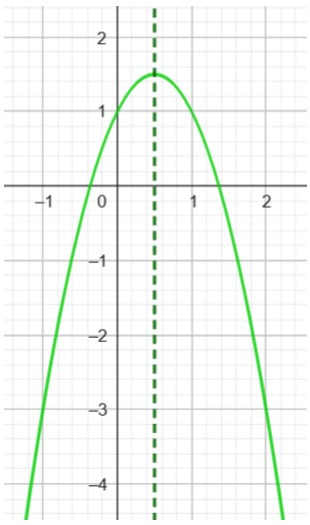
Coefficiente a negativo si traduce nell’avere la concavità rivolta verso il basso.
La parabola di equazione y = − x² è quella in rosso e la prendiamo come riferimento.
Tutte le parabole con coefficiente minore di −1 risultano essere meno aperte.
Tutte le parabole con coefficiente compreso tra −1 e 0 risultano essere molto più aperte. ​

Il coefficiente b ci dà indicazioni sulla posizione dell’asse di simmetria:

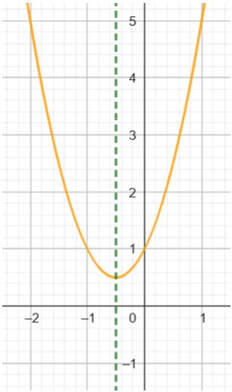
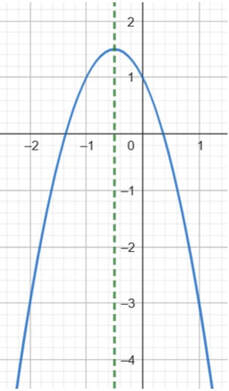
• se i coefficienti a e b sono concordi (hanno lo stesso segno) l’asse di simmetria della parabola è interamente contenuto nel semipiano delle ascisse negative;
• se il coefficiente b è uguale a zero, l’asse di simmetria della parabola coincide con l’asse y;
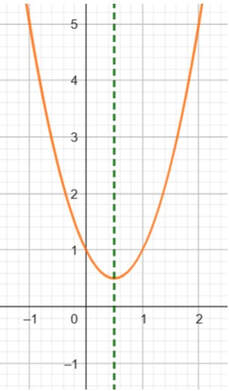
• se i coefficienti a e b sono discordi (hanno segno diverso) l’asse di simmetria della parabola è interamente contenuto nel semipiano delle ascisse positive. 

y = 2x² + 2x + 1
a e b concordi

y = 2x² – 2x + 1
a e b discordi

y = ​– 2x² + 2x + 1
a e b discordi

y = ​– 2x² – 2x + 1
a e b concordi

Il termine noto c

Tutte le parabole disegnate sopra hanno come termine noto c = 1, questo vuol dire che tutte le parabole sopra passano per il punto (0; 1).
Potremmo chiamare il termine noto, come nel caso della retta, è l'intercetta, perché ci dice, per parabole con asse parallelo all’asse y, in quale punto delle ordinate viene intercettata, è secante, la parabola. ​

Parabole particolari

Se b = c = 0 → y = ax²

La parabola ha vertice nell'origine degli assi, conseguentemente l'asse di simmetria è l'asse delle y.

Equazione dell’asse

x = 0

Equazione della direttrice

Coordinate del vertice

V = (0; 0)

Coordinate del fuoco

---

​Se c = 0 → y = ax² + bx

​La parabola passa per l’origine degli assi. 

Equazione dell’asse

Equazione della direttrice

Coordinate del vertice

Coordinate del fuoco

---

Se b = 0 → y = ax² + c

​È come la parabola y = ax² ma traslata verso l’alto, se c > 0, o traslata verso il basso, se c < 0.

Equazione dell’asse

x = 0

Equazione della direttrice

Coordinate del vertice

V = (0; c)

Coordinate del fuoco

Fasci di parabole

Date due parabole:

γ₁:    y = a₁x² + b₁x + c₁
γ₂:    y = a₂x² + b₂x + c₂

Si chiama fascio di parabole, generato dalle due parabole sopra, tutte le parabole che si ottengono dall’equazione: 

y − a₁x² − b₁x − c₁ + k(y − a₂x² − b₂x − c₂) = 0

da cui in forma esplicita

y + ky = a₁x² + a₂kx² + b₁x + b₂kx + c₁ + kc₂
(1 + k)y = (a₁ + a₂k)x² + (b₁ + b₂k)x + c₁ + kc₂

• Se k = −1 il coefficiente di y è annullato e tutto si riduce a un’equazione di secondo grado in una sola variabile, in questo caso quella x:
  - se il Δ > 0 abbiamo una parabola degenere rappresentata da due rette verticali
  - se Δ = 0 abbiamo una sola parabola degenere rappresentata da una sola retta verticale.

• Se k = −a₁/a₂  è il coefficiente al quadrato ad essere annullato. Otteniamo così l’equazione di una retta che è considerata altra parabola degenere appartenente al fascio di rette. 

Ponendo a sistema le equazioni delle due parabole generatrici possiamo ottenere:

• due punti di intersezione
  due punti base per i quali passano tutte le parabole del fascio
  
• un punto di intersezione
  un punto base per il quale passano tutte le parabole del fascio
  
• nessun punto di intersezione
  non esistono punti base
  

⚠ imponendo k = 0 otteniamo l’equazione della seconda parabola generatrice

Dai punti base all’equazione del fascio di parabole

Date due punti base, A e B, di un fascio di parabole è possibile determinare l’equazione del fascio procedendo in questo modo: 

1. determina l’equazione della retta passante per A e B:

    a) prima calcola il coefficiente angolare ​

    b) ora ricava l’equazione della retta esplicita utilizzando il coefficiente angolare m appena calcolato e le coordinante di uno dei due punti:

    c) scrivi in forma esplicita l’equazione della retta passante per A e B: 

2. l’equazione del fascio di parabole è dato dalla seguente formula: 

Un punto base – Retta tangente e punto di tangenza

Dato un punto base, T (xT; yT), corrispondente al punto di tangenza di tutte le rette del fascio, e all’equazione della retta tangente alla parabola che sto considerando otteniamo che, l’equazione generale del fascio, sia uguale a:

Sistemi retta-parabola

RETTA

Forma normale o implicita di una retta: ax + by + c =0

• se a = 0 allora dovrà essere b ≠ 0; 
  la retta è parallela all'asse x
• se b = 0 allora dovrà essere a ≠ 0; 
  la retta è parallela all'asse y
  
• se c = 0 la retta passa per l'origine degli assi cartesiani
  
• se a = 0 e c = 0 si tratta dell'asse x
  
• ​se b = 0 e c = 0 si tratta dell'asse y  

Forma esplicita di una retta: y = mx + q

PARABOLA

Forma esplicita di una parabola con asse di simmetria verticale (parallelo all'asse y):
y = ax² + bx + c    

• se a = 0 non è una parabola ma una retta
• se a > 0 le braccia della parabola vanno verso le y positive
• se a < 0 le braccia della parabola vanno verso le y negative
• se b = 0 l'asse di simmetria coincide con l'asse y
• il valore di c ci dice in quale punto la parabola incontra l'asse y

Forma esplicita di una parabola con asse di simmetria orizzontale (parallelo all'asse x):
x = ay² + by + c    

• se a = 0 non è una parabola ma una retta
• se a > 0 le braccia della parabola vanno verso le x positive
• se a < 0 le braccia della parabola vanno verso le x negative
• se b = 0 l'asse di simmetria coincide con l'asse x
• il valore di c ci dice in quale punto la parabola incontra l'asse x 

Risoluzione di problemi sulla parabola

Qui di seguito vi propongo alcuni video spiegazione sulla parabola. Spero possano esservi di aiuto

Pagina creata il 17 aprile 2023