Punti notevoli

PUNTI NOTEVOLI DI UN TRIANGOLO

BISETTRICI E INCENTRO

Bisettrice: retta che divide un angolo in due parti congruenti (della stessa ampiezza).

Incentro: il punto di incontro delle bisettrici di un triangolo.
Le bisettrici degli angoli interni di un triangolo sono sempre interne alla sua superficie.

Dopo aver trovato l'incentro di un triangolo, traccia ad esso la perpendicolare ad uno dei lati e metti in evidenza il punto di incontro: il segmento che ha come estremi l'incentro e il punto di intersezione trovato prima è il raggio della circonferenza inscritta al triangolo.

Provaci tu - disegna l'incentro

1) Strumento poligono

Disegna un triangolo qualunque e rendi evidenti le etichette dei vertici A, B e C.

2) Strumento bisettrici

Disegna le bisettrici: tre click nell'ordine sul punto A, B e C, poi su B, C e A, infine su C, A e B. La regola è: lato-vertice-lato.

3) Strumento punto

Metti in evidenza il punto di incontro delle bisettrici facendo un click sul punto preciso fino a quando non compare una manina con l'indice sollevato.
Hai disegnato l'INCENTRO.
Mostra l'etichetta dell'incentro e rinominalo chiamandolo O (usa il tasto destro del mouse quando fai il click).

4) strumento mostra/nascondi

Nascondi le tre bisettrici facendo un click su di esse. Un click sullo strumento muovi.

5) strumento perpendicolare

Un click sull'incentro, il punto interno al triangolo, e un altro click su uno dei tre lati.

6) Strumento punto

Metti in evidenza il punto di intersezione tra la perpendicolare e il lato.

7) strumento mostra nascondi

Nascondi la perpendicolare appena disegnata (quando usi lo strumento mostra/nascondi gli oggetti già nascosti appasiono grigi).

8) strumento circonferenza

Fai un click sul punto disegnato al passo 6) e un click sull'incentro.
Hai disegnato la circonferenza inscritta al triangolo.

Pulsante indietro/avanti
Se hai sbagliato o fatto un'operazione non voluta premi il tasto indietro.
Se sei tornato indietro troppe volte, allora puoi premere il pulsante avanti.

Quando selezioni questo pulsante puoi:

spostare gli oggetti non vincolati;
selezionare gli oggetti per poi modificarne le caratteristiche (colore, dimensione, ...).

Puoi modificare le caratteristiche di ciascun oggetto disegnato.

ALTEZZE E ORTOCENTRO

Altezza: segmento che ha come estremi un vertice e il piede della perpendicolare al lato opposto del vertice considerato.
Può essere definito anche come la distanza di un lato, o del suo prolungamento, dal vertice opposto.

In un triangolo rettangolo, i lati che formano l'angolo retto (cateti)sono altezze reciproche: un cateto è altezza del triangolo rispetto all'altro cateto.
L'altezza relativa al lato opposto all'angolo retto (ipotenusa) è sempre interna alla superficie del triangolo.

Ortocentro: punto d'incontro delle altezze di un triangolo o dei suoi prolungamenti.

Provaci tu - l'ortocentro

1) poligono

Disegna un triangolo qualunque.

2) perpendicolare

Un click su un vertice e un altro sul lato opposto (ricorda, solo quando compare la manina sei sicuro di aver selezionato l'oggetto giusto)

3) punto

Avvicina il mouse sull'intersezione tra le perpendicolari e fai un click (non spaventarti, questo luogo può essere anche molto distante al triangolo che hai disegnato).
Hai disegnato l'ortocentro.

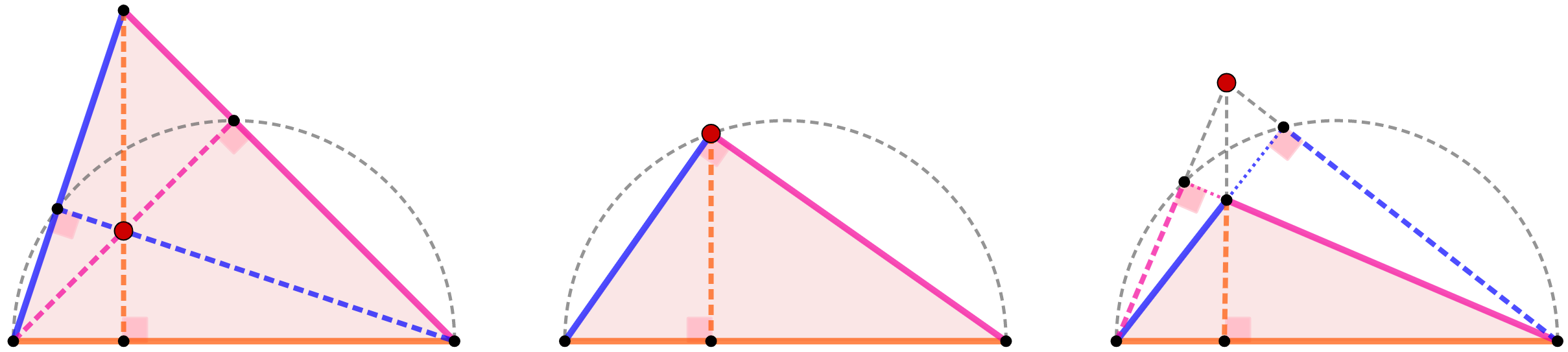
Ortocentro nel triangolo scaleno

Nel triangolo scalelo l'ortocentro può essere interno al suo perimetro (nel caso dell'acutangolo), coincidere con il vertice dell'angolo retto (nel triangolo rettangolo) o esterno al triangolo nel caso sia ottusangolo).

TRIANGOLO SCALENO ACUTANGOLO
L'ortocentro è interno al triangolo

TRIANGOLO SCALENO RETTANGOLO
L'ortocentro coincide con il vertice dell'angolo retto

TRIANGOLO SCALENO OTTUSANGOLO
L'ortocentro è esterno al triangolo

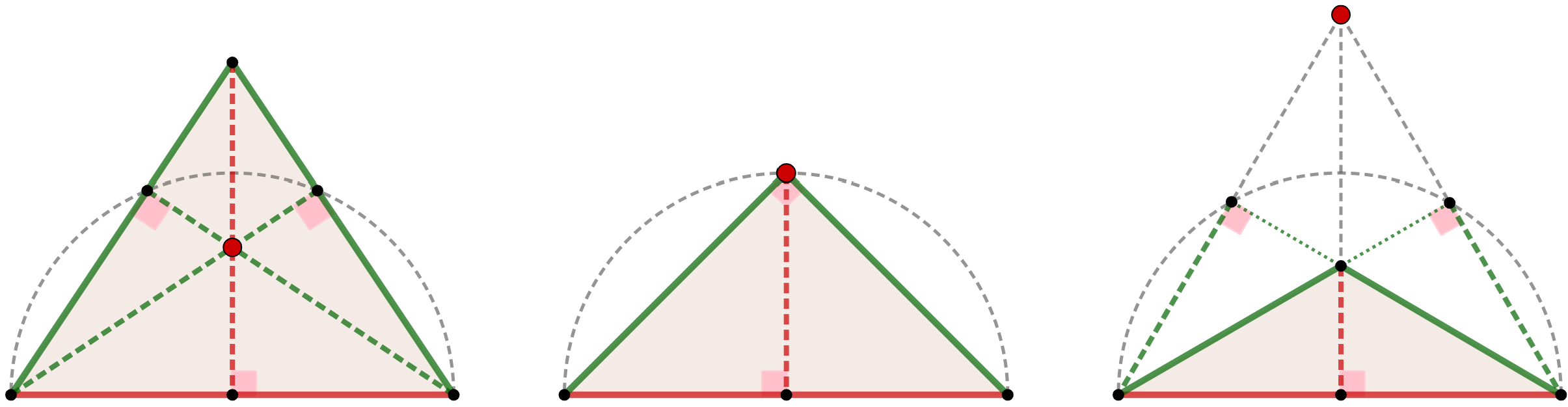
Ortocentro nel triangolo isoscele

Quanto abbiamo visto nel triangolo scaleno, accade anche nel triangolo isoscele.
Ortocentro interno al triangolo → acutangolo
Ortocentro coincidente con il vertice dell'angolo retto → rettangolo
Ortocentro esterno al triangolo → ottusangolo

TRIANGOLO ISOSCELE ACUTANGOLO
L'ortocentro è interno al triangolo

TRIANGOLO ISOSCELE RETTANGOLO
L'ortocentro coincide con il vertice dell'angolo retto

TRIANGOLO ISOSCELE OTTUSANGOLO
L'ortocentro è esterno al triangolo

MEDIANE E BARICENTRO

Mediana: segmento che ha per estremi un vertice e il punto medio del lato opposto.

Baricentro: il punto di incontro delle mediane in un triangolo.
Il baricentro è:

sempre interno alla superficie del triangolo;
un punto di equilibrio del triangolo stesso. Se costruiamo un triangolo qualunque omogeneo per spessore e materiale, è possibile mantenere orizzontale il triangolo tenendolo appeso per il suo baricentro.

Mediane e baricentro - Provaci tu

1) poligono

Disegna un triangolo qualunque.

2) punto medio

Un click su ciascun lato per disegnare i loro punti medi.

3) segmento

Ora disegniamo le mediane: un click su un vertice e un altro sul punto medio del lato opposto. Ripeti per tutti e tre i lati.

Punto

Avvicina il mouse sino al punto di intersezione delle tre mediane fino a quando non compare una manina, fai un click.

mostra/nascondi

Rendi invisibili i punti medi e le mediane.

selezione - la freccia

Sposta i vertici del triangolo e verifica se la costruzione è corretta.
Cosa puoi dire sulla posizione del baricentro?

ASSI E CIRCOCENTRO

Asse: retta perpendicolare ad un lato passante per il suo punto medio.

Circocentro: punto di incontro degli assi di un triangolo.
Il circocentro:

coincide con il punto medio dell'ipotenusa in un triangolo rettangolo;
è interno al triangolo nei triangoli acutangoli;
è esterno al triangolo nei triangoli ottusangoli.

Assi e circocentro - Provaci tu

1) strumento poligono

Disegna un triangolo qualunque

2) Punto medio

Con un click su ciascun lato (quando compare la manina) disegna i punti medi di ogni lato.

3) Perpendicolare

Un click nel punto medio e un altro nel lato che lo contiene.
Ripeti per ciascun lato

4) punto

Un click sul punto di intersezione degli assi appena disegnati.
Hai individuato il circocentro.

5) circonferenza

Un click sul circocentro e uno in uno dei vertici del triangolo.

6) mostra/nascondi

Rendi invisibili gli assi e i punti medi.

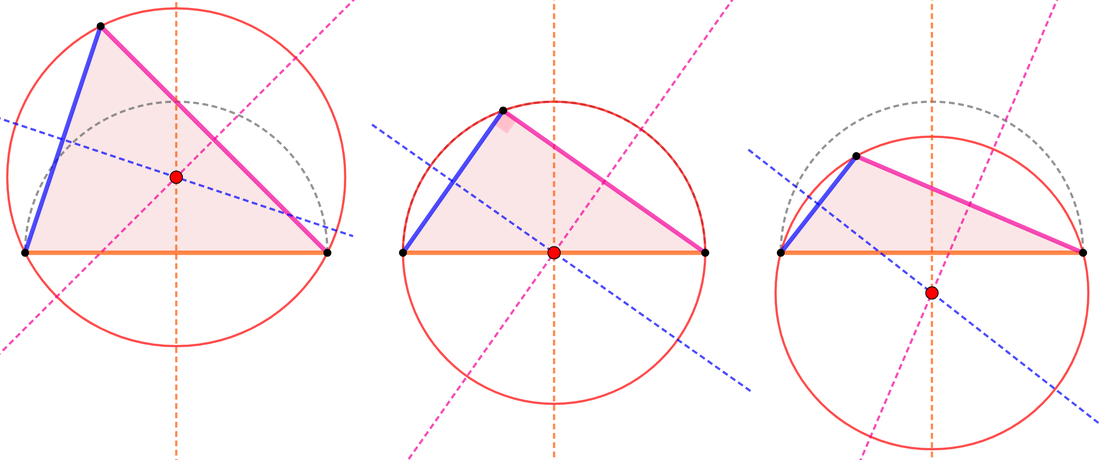
Circocentro nel triangolo scaleno

TRIANGOLO SCALENO ACUTANGOLO
Il circocentro sta dentro la superficie del triangolo, vicino al lato più lungo.

TRIANGOLO SCALENO RETTANGOLO
Il circocentro coincide con il punto medio del lato più lungo (l'ipotenusa).

TRIANGOLO SCALENO OTTUSANGOLO
Il circocentro si trova fuori dal triangolo, vicino al lato più lungo.

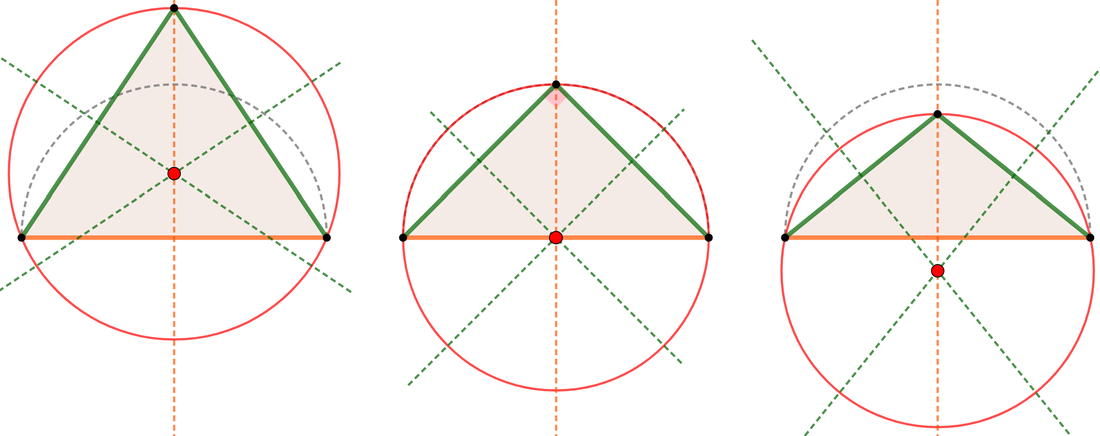
Circocentro nel triangolo isoscele

TRIANGOLO ISOSCELE ACUTANGOLO
Il circocentro sta dentro la superficie del triangolo, al di sopra della base.

TRIANGOLO ISOSCELE RETTANGOLO
Il circocentro coincide con il punto medio del lato più lungo (l'ipotenusa).

TRIANGOLO ISOSCELE OTTUSANGOLO
Il circocentro si trova fuori dal triangolo, vicino alla base.