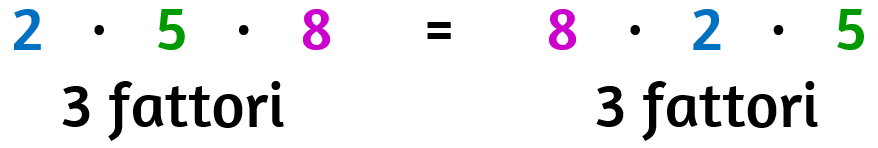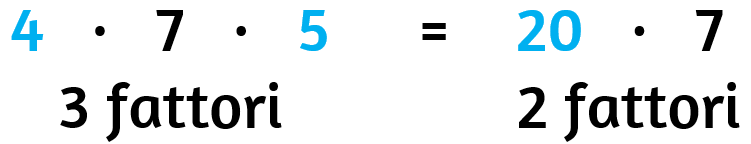LA MOLTIPLICAZIONE E LE SUE CARATTERISTICHE
|
La moltiplicazione è figlia dell’addizione, in quanto si tratta di un’addizione particolare, nella quale la prima quantità è ripetuta tante volte quanto indica la seconda quantità.
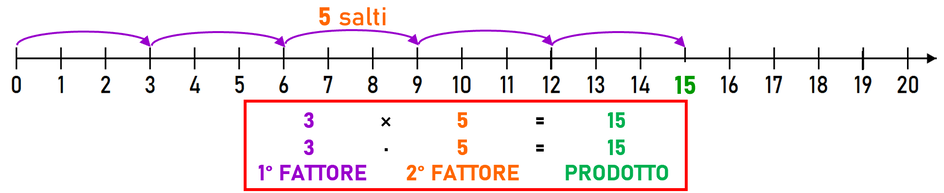
Fare una moltiplicazione vuol dire, dunque, ripetere una stessa quantità un certo numero di volte e considerarne la quantità totale ottenuta, il prodotto. 
Sulla retta dei numeri:
|
|
In "matematichese" viene così spiegata: "La moltiplicazione è l’operazione che consente di associare a due numeri, chiamati fattori, un terzo numero, chiamato prodotto, al quale si perviene addizionando tanti addendi uguali al primo numero quante sono le unità del secondo e così via".
L'operazione di addizione si dice interna all'insieme dei numeri naturali, ciò vuol dire che se tutti i fattori sono numeri naturali (interi e positivi) il prodotto sarà sempre un numero naturale.
L'1 e lo zero nella moltiplicazione
Se uno dei fattori è 1 il prodotto finale è uguale al prodotto di tutti gli altri fattori diversi da 1.
Il numero 1 è l’elemento neutro della moltiplicazione.
Elemento neutro: la sua presenza o la sua assenza non influenza il risultato finale.
Il numero 1 è l’elemento neutro della moltiplicazione.
Elemento neutro: la sua presenza o la sua assenza non influenza il risultato finale.
2 × 9 × 1 × 5 = 2 × 9 × 5
Se uno dei fattori è zero il prodotto finale è uguale a zero.
Lo zero è l’elemento assorbente della moltiplicazione.
Lo zero è l’elemento assorbente della moltiplicazione.
85 × 46 × 0 × 67 × 4 = 0
Se moltiplichiamo due numeri naturali otteniamo sempre un numero naturale:
tutte le moltiplicazioni sono possibili (nell’insieme dei numeri naturali).
Elemento assorbente: la sua presenza rende zero il risultato finale.
tutte le moltiplicazioni sono possibili (nell’insieme dei numeri naturali).
Elemento assorbente: la sua presenza rende zero il risultato finale.
Numeri pari e numeri dispari nella moltiplicazione
Che risultato otteniamo se moltiplichiamo un numero pari ad un numero dispari o quale altra combinazione?
In una moltiplicazione composta da più fattori:
- ottieni un numero dispari se tutti i fattori sono dispari;
- ottieni un numero pari se anche solo uno dei fattori è pari.
L'operazione inversa della moltiplicazione
La moltiplicazione ha come operazione inversa due divisioni:
|
|
Prima divisione inversa:
|
Seconda divisione inversa:
|
La tavola delle moltiplicazioni
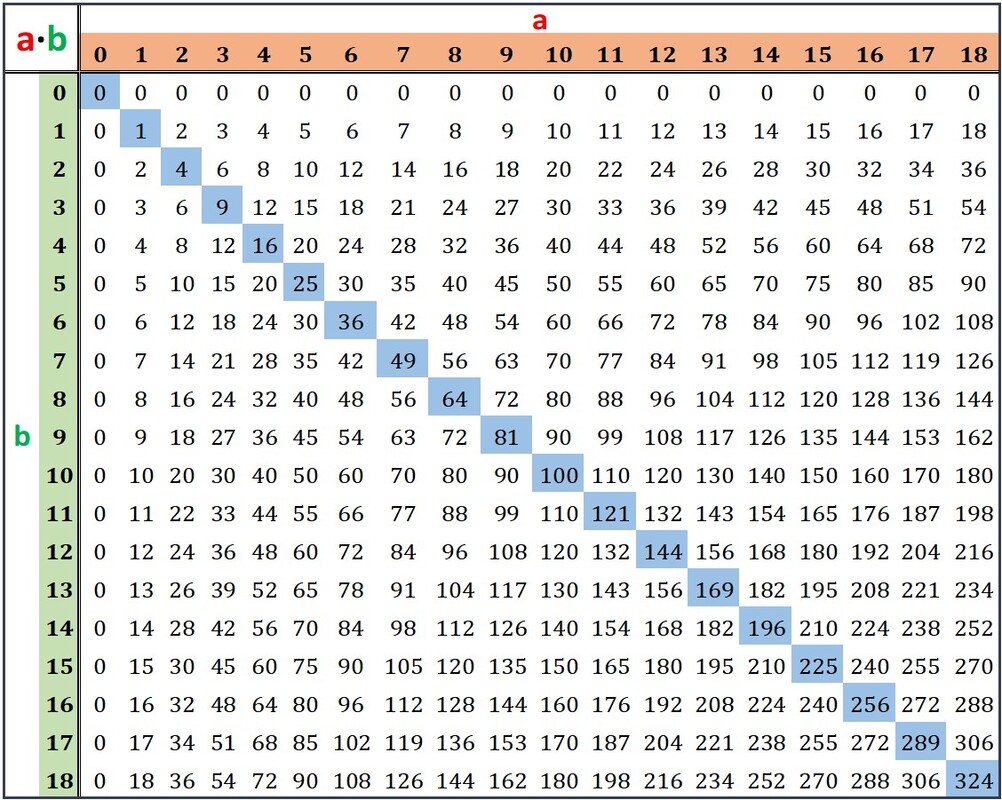
La tabella è simmetrica rispetto alla diagonale dei numeri evidenziati in azzurro, sottolineando che la moltiplicazione gode della proprietà commutativa.
La seconda riga e la seconda colonna compare sempre lo 0, in quanto rappresenta l'elemento assorbente, mentre la terza riga e terza colonna riportano i numeri dell’intestazione delle righe e delle colonne, ciò evidenzia che l’uno è l’elemento neutro della moltiplicazione.
Nota bene, nella diagonale in azzurro sono posti i quadrati dei numeri corrispondenti, quei numeri che si ottengono moltiplicando un numero per se stesso.
La seconda riga e la seconda colonna compare sempre lo 0, in quanto rappresenta l'elemento assorbente, mentre la terza riga e terza colonna riportano i numeri dell’intestazione delle righe e delle colonne, ciò evidenzia che l’uno è l’elemento neutro della moltiplicazione.
Nota bene, nella diagonale in azzurro sono posti i quadrati dei numeri corrispondenti, quei numeri che si ottengono moltiplicando un numero per se stesso.
COME FARE UNA MOLTIPLICAZIONE
L'algoritmo della moltiplicazione in colonna (con i riporti da ricordare) Metodo classico
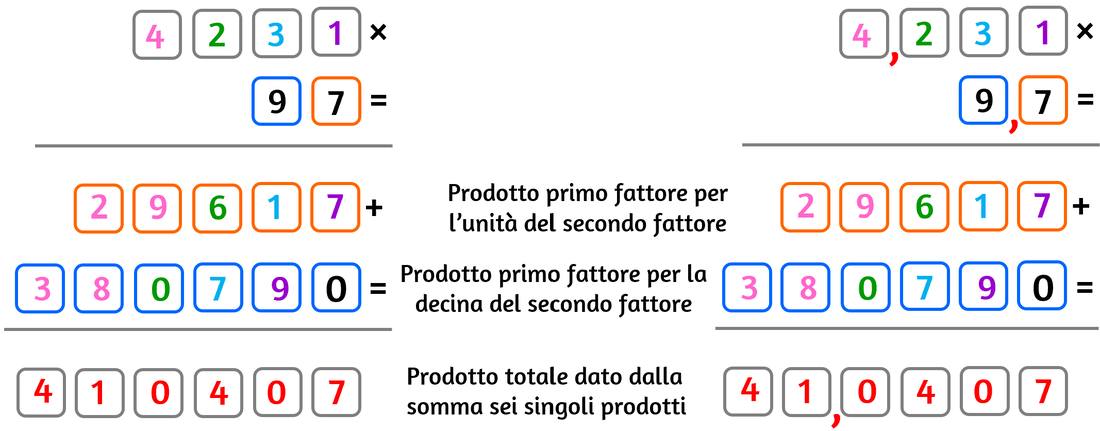
Il risultato si ottiene attraverso operazioni successive:
- moltiplico la prima cifra a destra del secondo fattore per tutto il primo fattore, il 7 moltiplicherà tutte le cifre del primo fattore partendo da destra (ricorda di sommare i riporti);
- scrivo il risultato sotto (riga con sfondo verde);
- moltiplico la seconda cifra del secondo fattore per tutto il primo fattore;
- scrivo il risultato sotto quello precedente, ma spostato di una cifra verso sinistra che occupo con uno zero;
- ripeto come sopra ma ad ogni cifra aumento gli spostamenti di una posizione verso sinistra.
- Ora le unità sono tutte sulla stessa colonna, come pure le decine, le centinaia, ..., e le sommiamo esattamente come si fa in un'addizione.
- Se uno o entrambi i fattori sono numeri decimali, eseguo la moltiplicazione così come indicato dal punto 1 al punto 6, infine disegno una virgola lasciando dopo di essa tante cifre quante in totale sono sono presenti in tutti i fattori.
|
Separa le cifre del risultato in classi per poterlo leggere meglio: 410'407.
|
In totale sono presenti 4 cifre decimali, tre nel primo fattore e una nel secondo fattore: il risultato finale avrà 4 cifre decimali: 41,0407.
|
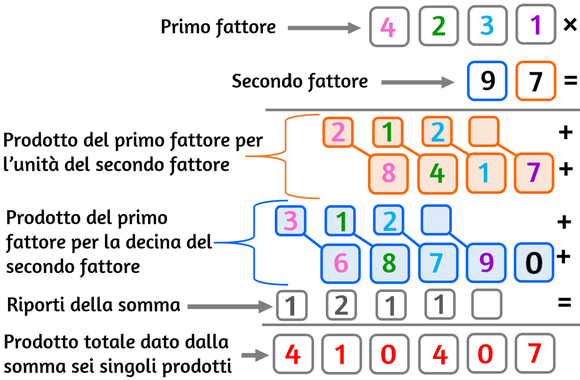
Moltiplicazione in colonna ma con i riporti da non tenere a mente
Supponiamo di voler eseguire 4231 × 97 =
scriviamo i risultati sulle caselle arancioni
scriviamo i risultati sulle caselle arancioni
- unità del 2° fattore per l'unità del 1° fattore → 7 × 1 = 7, scrivo 7
- unità del 2° fattore per la decina del 1° fattore → 7 × 3 = 21 scrivo 1 e riporto 2
- unità del 2° fattore per le centinaia del 1° fattore → 7 × 2 = 14 scrivo 4 e riporto 1
- unità del 2° fattore per le migliaia del 1° fattore → 7 × 4 = 28 scrivo 8 e riporto 2
- decina del 2° fattore per unità del 1° fattore → 9 × 1 = 9, scrivo 9
- decina del 2° fattore per decina del 1° fattore → 9 × 3 = 27 scrivo 7 e riporto 2
- decina del 2° fattore per centinaia del 1° fattore → 9 × 2 = 18 scrivo 8 e riporto 1
- decina del 2° fattore per migliaia del 1° fattore → 9 × 4 = 36 scrivo 6 e riporto 3
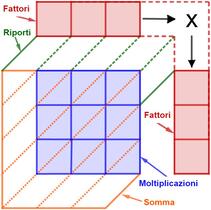
Metodo della graticola nella risoluzione delle moltiplicazioni
|
Vogliamo fare la moltiplicazione 3,64 x 42,5. Costruiamo un rettangolo avente come base tanti quadretti quante le cifre del primo fattore e come altezza tanti quadretti quante sono le cifre del secondo fattore. Costruite quindi la graticola dividendo poi ciascun quadretto secondo una diagonale.
|
|
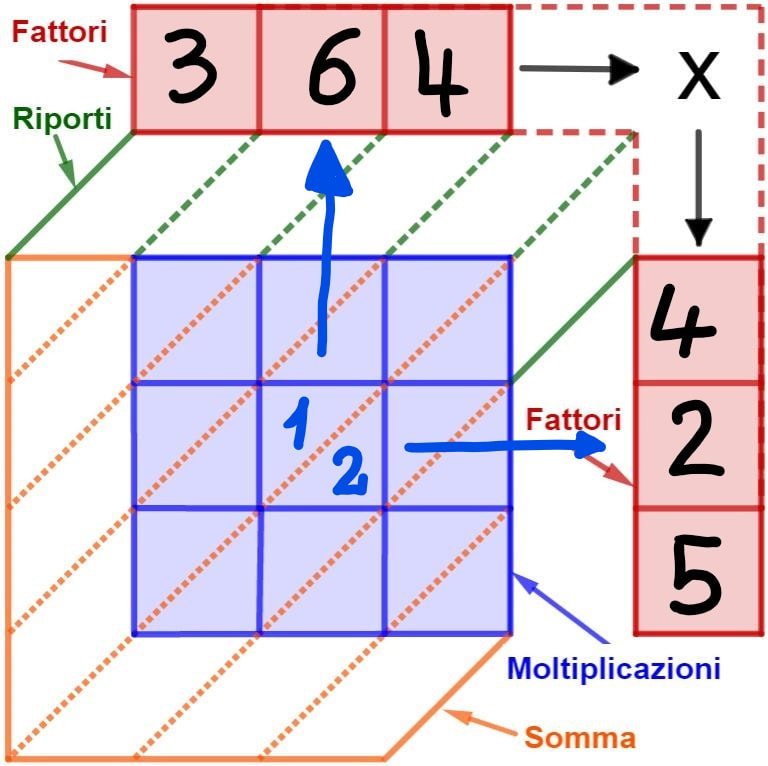
Scriviamo i due fattori della moltiplicazione: il primo fattore nella base superiore e il secondo fattore nell’altezza a destra, una cifra per ciascun quadretto. In ogni casella scrivete il prodotto delle cifre corrispondenti in alto e a destra, ponendo l’unità sulla destra e la decina sulla sinistra. Compilate tutta la graticola.
|
|
|
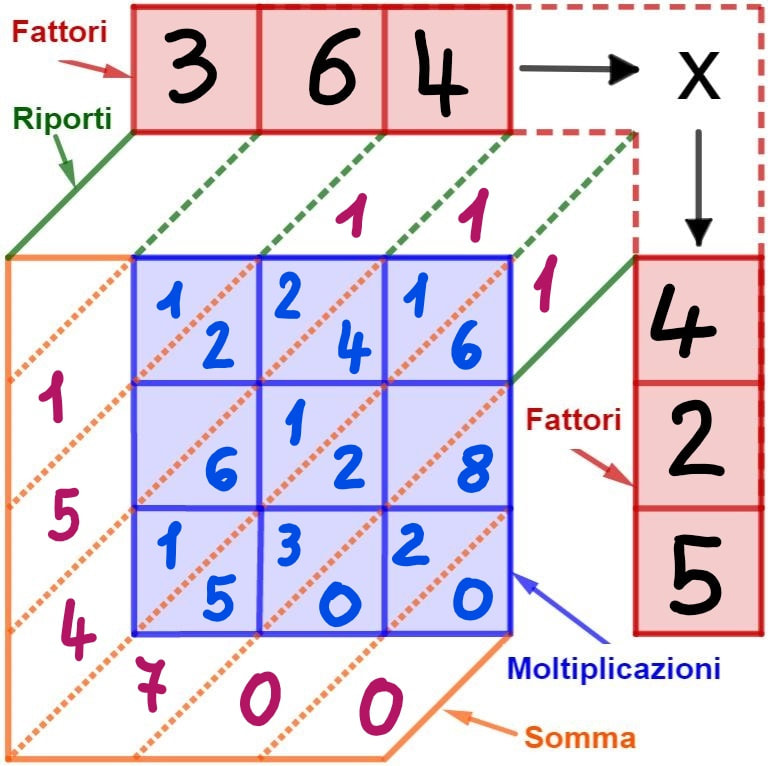
Ora sommate tutte le cifre che si trovano in ciascuna diagonale partendo dalla prima in basso a destra, trascrivendo solo la cifra delle unità e di sommare alla colonna successiva il rispettivo riporto, continuando fino all’ultima in alto a sinistra.
Se uno o entrambi i fattori sono numeri con la virgola, il procedimento è lo stesso, con la differenza che il prodotto avrà tante cifre dopo la virgola quante ne avevano in tutto i numeri originali. |
|
364 · 425 = 154700
|
così
|
3,64·42,5 =
= 154,700 = = 154,7 |
3,64 ha 2 cifre decimali, mentre 42,5 ha 1 cifra decimale
3 cifre decimali in tutto, 3 cifre dopo la virgola ho tolto gli zeri inutili |
Moltiplicare un numero per 10, 100, 1000
Quando moltiplico un numero per 10 ciascuna cifra aumenta il proprio valore di un ordine di grandezza: le centinaia diventano migliaia, le decine diventano centinaia, le unità diventano decine, i decimi diventano unità, ...
Quando moltiplico un numero per 100 ciascuna cifra aumenta il proprio valore di due ordini di grandezza.
Da qui la regola:
quando moltiplico un numero per 10, 100, 1000, 10000, ... ciascuna cifra del primo fattore aumenta il proprio valore di tanti ordini di grandezza quanti sono gli zeri presenti nel secondo fattore.
quando moltiplico un numero per 10, 100, 1000, 10000, ... ciascuna cifra del primo fattore aumenta il proprio valore di tanti ordini di grandezza quanti sono gli zeri presenti nel secondo fattore.
Moltiplicare un numero naturale (intero) per 10, 100, 1000, …
|
|
Moltiplicare un numero decimale per 10, 100, 1000, …
|
|
LE PROPRIETÀ DELLA MOLTIPLICAZIONE
Le proprietà sono modifiche che posso apportare ai fattori ma che non cambiano il risultato finale.
In questo modo le proprietà diventano degli strumenti che possono semplificare i calcoli e permettere così di fare a mente operazioni che diversamente avremmo dovuto risolverle in colonna o con altri metodi.
Vediamole un pochino.
In questo modo le proprietà diventano degli strumenti che possono semplificare i calcoli e permettere così di fare a mente operazioni che diversamente avremmo dovuto risolverle in colonna o con altri metodi.
Vediamole un pochino.
Proprietà commutativa (commutare = cambiare la posizione)
Cambiando l'ordine dei fattori il prodotto non cambia.
Cambio l'ordine dei termini della moltiplicazione.
Il numero dei fattori rimane uguale.
Cambio l'ordine dei termini della moltiplicazione.
Il numero dei fattori rimane uguale.
|
|
|
|
Proprietà associativa (associare = mettere insieme)
Il prodotto di tre o più fattori non cambia
se a questi si sostituisce il prodotto di due o più di loro.
Riscrivo un fattore con un'altra moltiplicazione.
Il numero dei fattori aumenta.
se a questi si sostituisce il prodotto di due o più di loro.
Riscrivo un fattore con un'altra moltiplicazione.
Il numero dei fattori aumenta.
|
|
|
|
Proprietà distributiva (distribuire = dare agli altri)
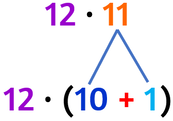
Proprietà distributiva rispetto all'addizione
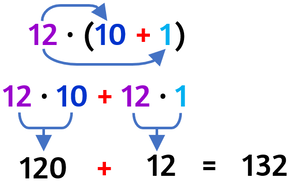
Il prodotto tra un numero ed un’addizione non cambia se, anziché moltiplicare il numero per la somma, moltiplichi il numero per ciascun termine dell’addizione e poi addizioni i risultati ottenuti.
Riscrivo un fattore come un'addizione dentro una parentesi.
|
|
|
|
Moltiplico il fattore non scomposto per ciascun addendo:
|
Eseguo l'addizione
|
|
|
Clicca sul link sotto per comprendere meglio questa proprietà.
https://apps.mathlearningcenter.org/partial-product-finder/
https://apps.mathlearningcenter.org/partial-product-finder/
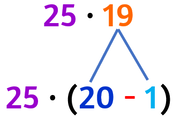
Proprietà distributiva rispetto alla sottrazione
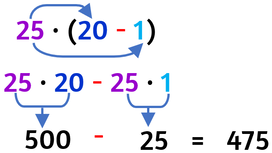
Il prodotto un numero ed una sottrazione non cambia se, anziché moltiplicare il numero per la differenza, moltiplichi il numero per ciascun termine della sottrazione e poi sottrai i dei due prodotti.
Riscrivo un fattore come una sottrazione dentro una parentesi.
|
|
|
|
Moltiplico il fattore non scomposto per ciascun termine della sottrazione:
|
Eseguo la sottrazione
|
|
|