CARATTERISTICHE GENERALI DEI QUADRILATERI
Caratteristiche generali a tutti i quadrilateri
|
Si chiama quadrilatero quel poligono che ha quattro lati.
AB, BC, CD e DA sono i lati del quadrilatero. |
La somma degli angoli interni, in un qualunque quadrilatero, è sempre di 360°.
α + β + γ + δ = 360° |
I TRAPEZI
Tutti i trapezi sono quadrilateri
e hanno le stesse caratteristiche generali dei quadrilateri.
e hanno le stesse caratteristiche generali dei quadrilateri.
Il trapezio ha due lati paralleli che si chiamano basi → AB⫽CD
I lati non paralleli si chiamano lati obliqui.
La somma degli angoli adiacenti a ciascun lato obliquo è 180° (gli angoli che poggiano ai lati non paralleli sono supplementari)
α + δ = β + γ =180°
Altezza del trapezio: distanza tra le basi o tra i suoi prolungamenti.
I lati non paralleli si chiamano lati obliqui.
La somma degli angoli adiacenti a ciascun lato obliquo è 180° (gli angoli che poggiano ai lati non paralleli sono supplementari)
α + δ = β + γ =180°
Altezza del trapezio: distanza tra le basi o tra i suoi prolungamenti.
|
Scaleno
|
Rettangolo
|
Isoscele
|
Trapezio scaleno
Provaci tu - Disegniamo un trapezio scaleno
|
1 - Retta
Disegna una retta qualunque 2 - retta parallela
Un click sulla retta appena disegnata e un altro nel foglio bianco in alto sulla destra. 3 - punto
Un click sulla seconda retta disegnata alla sinistra del punto C. 4 - poligono
Un click in ciascun punto disegnato nell'ordine A, B, C, D e infine nuovamente su A. |
5- Retta perpendicolare
Un click sulla retta in basso esternamente al trapezio appena disegnato e un altro nell'altra retta parallela posta sopra. 6 - Punto
Un click dove la nuova perpendicolare incontra la prima retta. 7 - Segmento
Un click nel punto E e un altro nel punto F. 8 - mostra/nascondi
Nascondi tutte le rette tranne il poligono e la distanza appena disegnata. |
Strumento muovi: un click su ciascun oggetto (lato o altezza) e modificane l'aspetto assegnando a ciascuno un colore diverso.
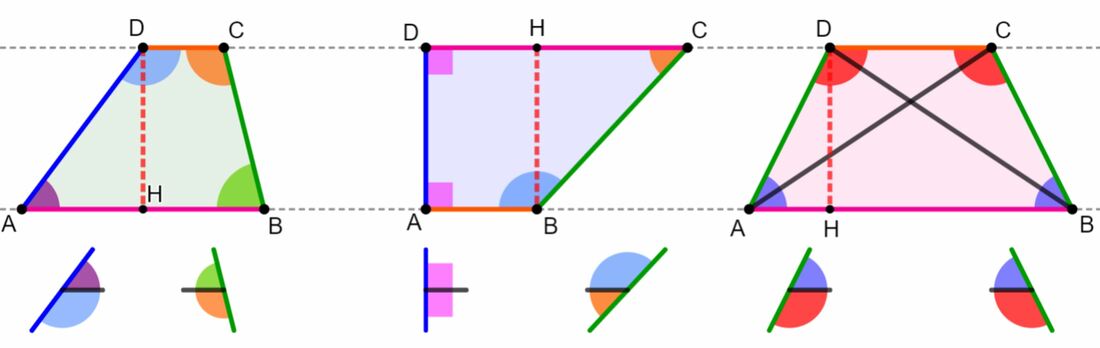
Trapezio rettangolo
|
Un lato obliquo è perpendicolare alle basi, per cui ci sono due angoli retti.
AB⊥AD e AD⊥CD |
L'altezza corrisponde al lato obliquo minore.
|
Provaci tu - Disegniamo un trapezio rettangolo
|
1 - retta
Disegna una retta. Compariranno i punti A e B. 2 - retta parallela
Un click sulla retta appena disegnata e un altro sul foglio nella parte alta a destra (comparirà il punto C). 3 - retta perpendicolare
Un click nel punto A e un altro nella retta parallela a quella che contiene il punto A. 4 - punto
Un click nel punto di intersezione tra la retta g e la retta h (la seconda retta parallela e quella perpendicolare alle due). Comparirà il punto D. 5 - Retta perpendicolare
Un click sulla retta parallela bassa e un altro in un suo punto a destra del punto B. Comparirà il punto E. |
6 - punto
Un click sulla retta perpendicolare che passa per E ma nel punto di intersezione con l'altra parallela, comparirà il punto F. 7 - segmento
Un click nel punto E e un altro nel punto F. 8 - poligono
Un click sui punti A, B, C, D e nuovamente su A, esattamente in quest'ordine. 9 - mostra/nascondi
Nascondi tutte le rette. 10 - muovi
Modifica le caratteristiche degli oggetti: I lati spessore 10 e di colore diverso. L'altezza, scegli un colore di tuo piacimento e rendi la linea tratteggiata. |
Trapezio isoscele
|
I lati obliqui sono congruenti.
BC≅AD |
Gli angoli adiacenti a ciascuna base sono congruenti.
α ≅ β e γ ≅ δ |
Le diagonali sono congruenti.
AC≅BD |
Provaci tu - Disegniamo un trapezio isoscele
|
1 - retta
Disegna una retta 2 - circonferenza
Un click sul punto A e un altro sul punto B. 3 - muovi
Col tasto destro un click sul punto A, vai su rinomina e chiamalo O. 4 - punto
Un click dove la circonferenza e la retta si incontrano (comparirà il punto A). 5 - retta perpendicolare
Un click sul punto O e un altro sulla retta. 6 - retta parallela
Un click sulla retta f e un altro sulla retta g. 7 - muovi
Col tasto destro un click sul punto C, vai su rinomina e chiamalo P. 8 - punto
Un click sulla parte a destra della nuova retta parallela (a destra del punto P), comparirà il punto C. 9 - circonferenza
Un click sul punto P e un altro sul punto C. |
10 - punto
Un click dove la nuova circonferenza e la retta parallela si incontrano a sinistra (comparirà il punto D). 11 - punto
Un click sulla retta parallela posta in basso esternamente alle due circonferenze (comparirà il punto E). 12 - retta perpendicolare
Un click sul punto E e un altro sulla retta che lo contiene. 13 - punto
Un click sulla retta che contiene il punto E ma al di sopra dove incontra la retta parallela. 14 - mostra/nascondi
Un click su tutte le rette e sui puti P e O. 15 - poligono
Un click sui punti A, B, C, D e A, esattamente in quest'ordine. 16 - segmento
Un click sui punti E e F. 17 - muovi
Modifica le caratteristiche dei lati facendoli diventare con spessore 10. Colora i lati obliqui di blu, la base maggiore di verde, la base minore di fucsia e la distanza di rosso con stile tratteggio. |
Attività - Le parti di un trapezio
|
Nei seguenti trapezi colora:
Ricorda, l'altezza nel trapezio è quel segmento che unisce le due basi (o i loro prolungamenti) perpendicolarmente (formando angoli di 90°). |
|
PARALLELOGRAMMI
Tutti i parallelogrammi sono anche trapezi scaleni e ne ereditano tutte le caratteristiche, ma ne possiedono delle altre in più:
|
I lati opposti sono paralleli.
Il lati opposti sono congruenti Gli angoli adiacenti a ciascun lato sono supplementari. Gli angoli opposti sono congruenti. Le diagonali si incontrano nel loro punto medio. |
AB||CD e BC||AD
AB≅CD e BC≅AD α + β = β + γ = γ + δ = δ + α = 180° α≅γ e β≅δ AM≅MC e BM≅MD |
Le caratteristiche dei trapezi isoscele e rettangolo non sono ereditate dai parallelogrammi, pertanto costituiscono un gruppo a sé.
ROMBI
Tutti i ROMBI sono parallelogrammi e trapezi e ne ereditano tutte le caratteristiche, ma ne possiedono altre in più:
|
Ha le diagonali perpendicolari.
I lati sono congruenti. |
→ AC ⊥ BD
→ AB ≅ BC ≅ CD ≅ DA |
RETTANGOLI
Tutti i RETTANGOLI sono anche parallelogrammi e trapezi, e ne ereditano tutte le loro caratteristiche, ma ne possiedono in più:
|
le diagonali sono congruenti
ogni lato è perpendicolare al suo consecutivo tutti gli angoli interni sono retti |
→
→ → |
AC ≅ BD
AB ⊥ BC ⊥ CD ⊥ DA α ≅ β ≅ γ ≅ δ = 90° |
Esiste sempre una circonferenza circoscritta al rettangolo
(cioè che tocca contemporaneamente tutti i vertici)
(cioè che tocca contemporaneamente tutti i vertici)
QUADRATI
Tutti i QUADRATI sono anche rettangoli, rombi, parallelogrammi e trapezi e ne ereditano tutte le loro caratteristiche:
come i trapezi hanno:
- due lati paralleli
- le coppie di lati opposti sia parallele che congruenti
- gli angoli adiacenti a ciasun lato sono supplementari (la loro somma è 180°)
- le diagonali che si incontrano nei rispettivi punti medi
- le diagonali perpendicolari → AC⊥BD
- i lati congruenti → AB≅BC≅CD≅DA
- esiste sempre una circonferenza circoscritta (che ha centro dove le diagonali si incontrano e passa per i vertici)
- le diagonali congruenti → AC≅BD
- i lati perpendicolari → AB⊥BC⊥CD⊥DA
- esiste sempre una circonferenza inscritta (che ha centro dove le diagonali si incontrano e tocca ciascun lato)
Aquiloni - Romboidi - Deltoidi
https://apps.mathlearningcenter.org/math-clock/
Clicca qui per modificare.
Contatore messo in data 22 febbraio 2021