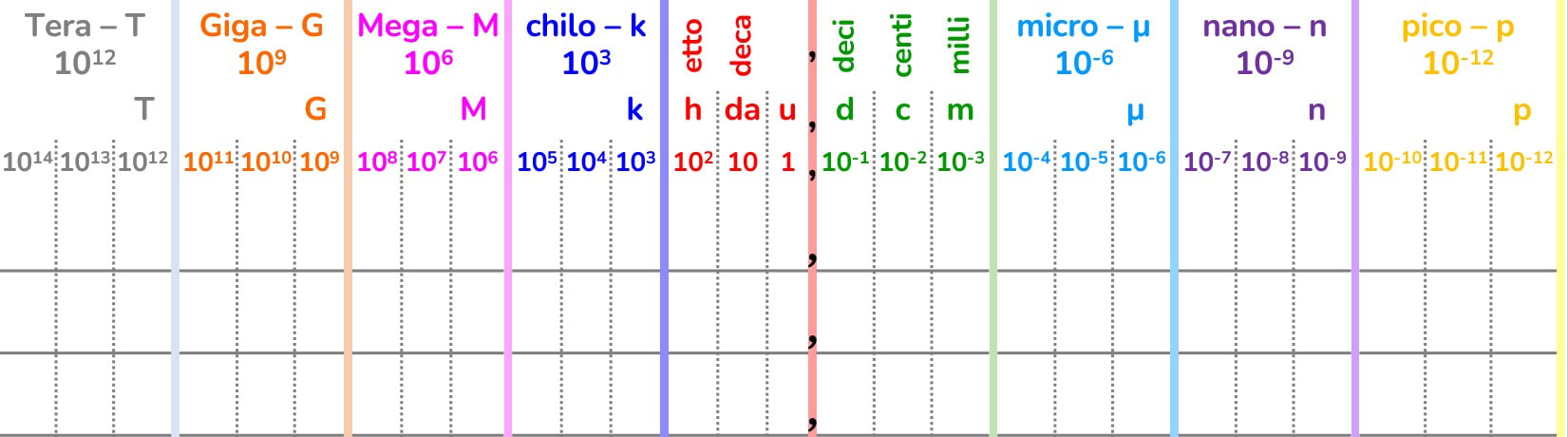
Le potenze di 10, la notazione scientifica e l'ordine di grandezza

Dalle potenze di 10 al loro valore e viceversa

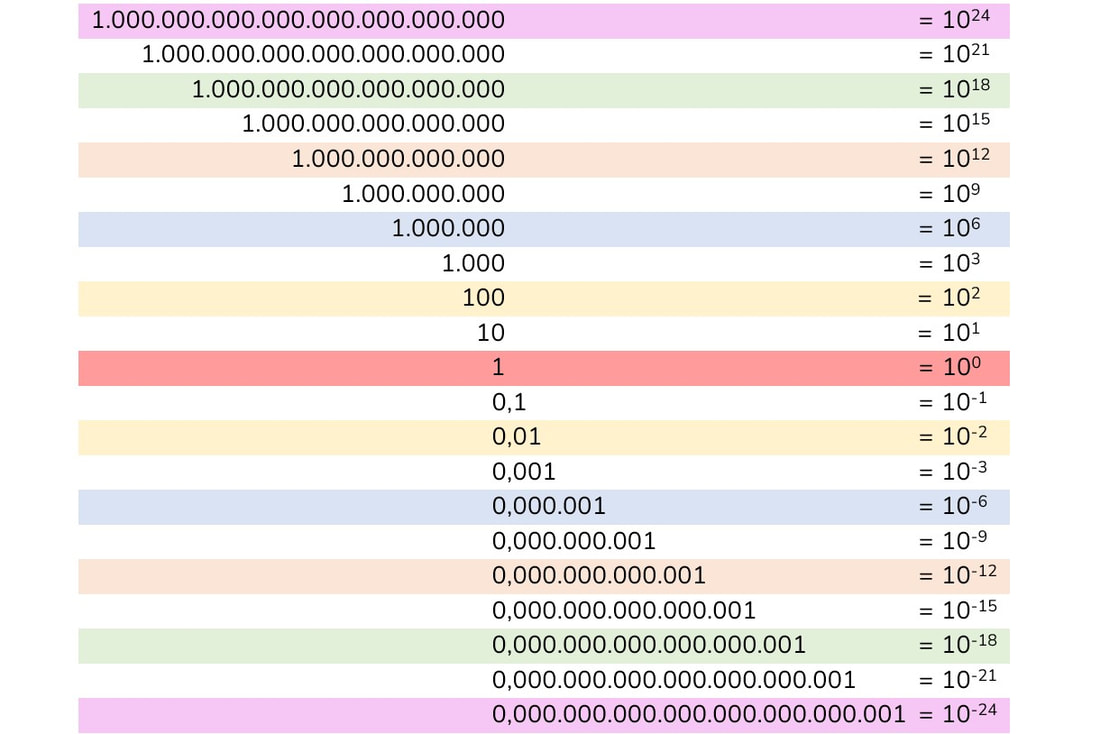
A potenze di 10 con esponente positivo è abbinato un numero maggiore o uguale a 1.
A potenze di 10 con esponente negativo è abbinato un numero decimale sempre più vicino a zero quanto più grande è l'esponente abbinato al segno meno. 

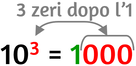
Quando una potenza ha come base 10 e come esponente un numero naturale ricorda:

1. scrivi un 1
2. scrivi di fianco all’1 tanti zeri quanto indica l’esponente

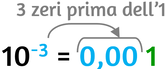
Quando una potenza ha come base 10 e come esponente un numero decimale ricorda:

1. scrivi tanti zeri quanto indica l’esponente
2. scrivi un 1
3. metti una virgola subito dopo il primo zero

I numeri in notazione scientifica

Leggere un numero molto grande o molto piccolo è talvolta difficile da fare, ed è per questo che per le misure sono state inventati i multipli e i sottomultipli.

Talvolta, però, il riferimento al multiplo (per i numeri molto grandi) o al sottomultiplo (per i numeri moto vicini allo zero e per cui molto piccoli) non è di immediata comprensione per cui riferirsi alla potenza di 10 più vicina è sicuramente più semplice e veloce. 

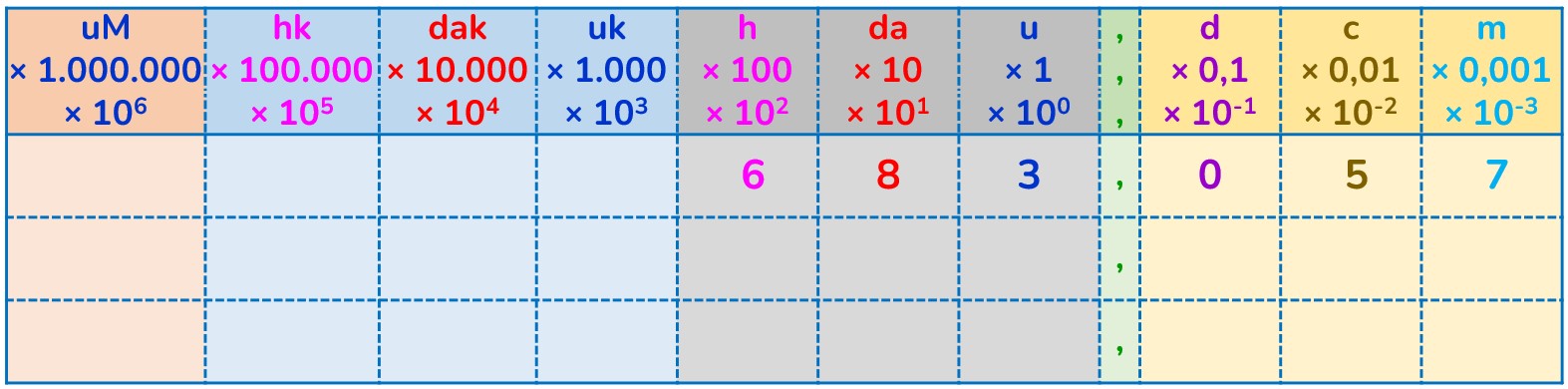
683,057 = 6,83057 · 10²

Scrivere un numero in notazione scientifica vuol dire scrivere una moltiplicazione nella quale:

• il primo fattore è un numero maggiore o uguale a 1 e minore di 10;
• il secondo fattore è una potenza di 10 che può avere come esponente un intero:
  - positivo (sottinteso) → se il numero originale è maggiore di 1;
  - negativo → se il numero originale è compreso tra 0 e 1. 

Scriviamo in notazione scientifica il numero 89 746

1. metti la virgola dopo la prima cifra a sinistra
2. metti il segno di moltiplicazione
3. scrivi 10
4. di quante cifre si è spostata un’ipotetica virgola posta a destra?
   quattro posti: 
   - virgola verso sinistra → nessun segno
   ​- virgola verso destra → segno meno
5. metti come esponente il numero il 4

Risultato sulla calcolatrice: 8,9746 E +4
Come immettere il risultato in un foglio di calcolo: 8,9746*10^4 

---

Scriviamo in notazione scientifica il numero 0,00935

1. sposta la virgola dopo la prima cifra diversa da zero (partendo da sinistra e andando verso destra)
2. metti il segno di moltiplicazione
3. scrivi 10
4. di quante cifre si è spostata la virgola? di 3 posti
   - virgola verso sinistra → nessun segno
   - virgola verso destra → segno meno
5. metti come esponente il segno meno «-» e come numero il numero 3

Risultato sulla calcolatrice: 9,35 E -3
Come immettere il risultato in un foglio di calcolo: 9,35*10^(-3) 

---

---

Dalla notazione scientifica all'ordine di grandezza

Definire l’ordine di grandezza di un numero è dare un’indicazione a quale potenza di 10 quella determinata quantità si avvicina di più.
Per conoscere l’ordine di grandezza di un numero dovremo:

• scrivere il numero in notazione scientifica
• controllare il primo fattore, se la parte intera del primo fattore è

1    2    3    4 

5    6    7    8    9

ordine di grandezza uguale al secondo fattore (potenza di 10)

​con lo stesso esponente

​con l'esponente aumentato di 1

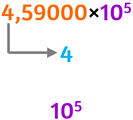
Determiniamo l’ordine di grandezza del numero 459 000

1. Scrivi il numero in notazione scientifica
2. La parte intera del primo fattore è 4
3. L’ordine di grandezza sarà uguale al secondo fattore con lo stesso esponente

---

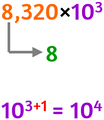
Determiniamo l’ordine di grandezza del numero 8 320

1. Scrivi il numero in notazione scientifica
2. La parte intera del primo fattore è 8
3. L’ordine di grandezza sarà uguale al secondo fattore ma con lo stesso esponente aumentato di 1.

---

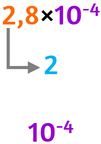
Determiniamo l’ordine di grandezza del numero 0,00028

1. Scrivi il numero in notazione scientifica
2. La parte intera del primo fattore è 2
3. L’ordine di grandezza sarà uguale al secondo fattore con lo stesso esponente

---

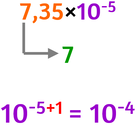
Determiniamo l’ordine di grandezza del numero 0,0000735

1. Scrivi il numero in notazione scientifica
2. La parte intera del primo fattore è 7
3. L’ordine di grandezza sarà uguale al secondo fattore ma con lo stesso esponente aumentato di 1

---

---

Contatore inserito il 11 agosto 2021