La statistica e gli indicatori statistici
Def. Si chiama statistica quella parte della matematica che si occupa di raccogliere, ordinare, riassumere, presentare e analizzare i dati.
La statistica si occupa di studiare e analizzare fenomeni che riguardano insiemi numerosi (gruppi di oggetti, animali, piante, persone, …) con l’obiettivo di capire meglio il fenomeno stesso, prevederne gli esiti futuri e magari individuare delle leggi che li regolano.
Fare un’indagine statistica vuol dire raccogliere delle informazioni di tipo qualitativo o quantitativo sul campione o l’intera quantità di soggetti da analizzare.
Nel raccogliere i dati riguardo alle caratteristiche di un gruppo di individui o di oggetti, è spesso impossibile o poco pratico osservare l'intero gruppo, specialmente se è grande. Invece di analizzare l'intero gruppo, chiamato popolazione o universo, si esamina una piccola parte del gruppo, chiamata campione.
Esempi di popolazione sono:
- gli alunni di una classe;
- gli alunni di una scuola;
- l’insieme delle penne prodotte da un’azienda;
- l’insieme delle specie animali in un parco naturale;
- gli abitanti di una città in una determinata data;
- i bulloni prodotti in un giorno in una giornata precisa;
- gli stipendi di tutti gli abitanti di una data regione...
Quando non è possibile fare un’indagine statistica in tutti gli elementi allora si può decidere di analizzare il fenomeno solo su una sua parte, che prende il nome di campione. La parte scelta che rappresenta la popolazione dovrebbe essere accuratamente scelta di modo da non falsare i risultati che si otterranno.
Variabili quantitative e variabili qualitative
Qualunque cosa oggetto dell’indagine statistica viene denominata variabile (= le caratteristiche che vengono prese in considerazione), mentre i valori registrati per ciascuna variabile sono denominati dati statistici.
|
Variabili qualitative
Tutto ciò che può essere espresso da un nome o un aggettivo. I valori che può assumere non sono numeri ma delle qualità come il colore, il gusto, il gradimento, il genere. Sono esempi di variabili qualitative:
|
Variabili quantitative
Tutto ciò che esprimibile con un numero, come semplici quantità o misure. I valori sono numerici e possono essere rappresentati da qualunque tipo di numero (naturale, razionale, irrazionale, …). Sono esempi di variabili quantitative:
|
Variabili discrete e variabili continue
Le variabili quantitative danno sempre origine a dati numerici che possono essere solo numeri interi o quantità che possono variare all’interno di un determinato range assumendone tutti i valori in quell’intervallo.
|
Variabili quantitative discrete
I valori sono rappresentati solo da una quantità finita di numeri interi:
|
Variabili quantitative continue
I valori sono rappresentati da numeri interi e/o decimali:
|
Elaborazione e rappresentazione dei dati
Il momento dell'elaborazione dei dati è veramente importante, in essa i dati acquisiti verranno catalogati, trascritti in apposite tabelle, per poi infine rappresentarli graficamente nei più svariati modi per poterli, così, interpretare.
A seconda dei dati statistici raccolti, possiamo creare vari tipi di tabelle.
A seconda dei dati statistici raccolti, possiamo creare vari tipi di tabelle.
Dato statistico: qualsiasi informazione di cui si conosce il numero di volte con cui si ripete in un indagine.
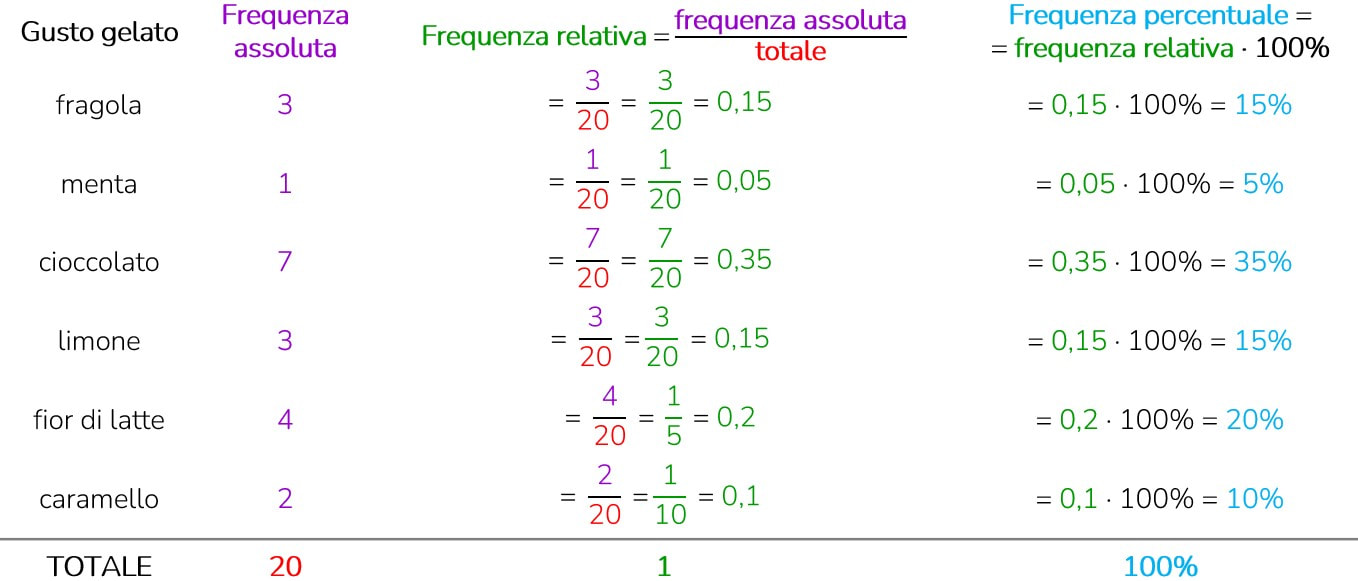
Frequenza assoluta, relativa e percentuale
In una classe di 20 alunni è stato richiesto quale fosse il gusto di gelato preferito, ecco l’elenco dei risultati ottenuti: fragola, menta, cioccolato, limone, fragola, fior di latte, fior di latte, cioccolato, caramello, cioccolato, limone, fior di latte, cioccolato, fragola, caramello, fior di latte, cioccolato, cioccolato, limone, cioccolato.
Frequenza assoluta: la quantità di volte con cui un determinato dato si presenta.
Costruiamo una tabella nella quale mettere nella prima colonna il gusto del gelato e nella seconda colonna la corrispondente quantità di alunni che hanno scelto quel gusto.
Frequenza relativa: rappresenta il rapporto tra la frequenza assoluta e il totale dei dati analizzati nell’indagine statistica. La frequenza relativa può essere data come rapporto ridotto ai minimi termini o come decimale.
Frequenza percentuale: è uguale al valore della frequenza relativa espressa come percentuale.
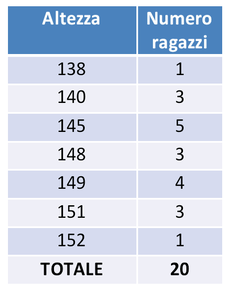
Tabella semplice (o tabella di frequenza assoluta)
|
Supponiamo di aver indagato sul fenomeno "altezza dei ragazzi della classe III di una scuola media" e di aver raccolto informzioni relative a 20 campioni scelti.
La tabella a destra mostra i dati raccolti per ciascun alunno. Successivamente deciadiamo di realizzare una tabella nella quale vogliamo mettere in evidenza la frequenza di una determinata altezza misurata nei componenti la classe III in esame, disponendo i dati in ordine crescente (dal più piccolo al più grande). La tabella ottenuta sarà: 
La tabella così ottenuta ci permette di darci informazioni più immediate, rispetto alla tabella precedente.
I dati riportati nella seconda colonna "Numero ragazz#" rappresentano la frequenza assoluta di ciascun dato (Altezza), cioè il numero di volte con cui un determinato dato si presenta in un indagine. |
|
I dati così ottenuti nella seconda tabella possono essere così interpretati:
- 1 alunno ha un altezza di 138 cm;
- 3 alunni hanno un altezza di 140 cm;
- 5 alunni hanno un'altezza di 145 cm;
- ....
- 1 alunno ha un altezza di 138 cm;
- 3 alunni hanno un altezza di 140 cm;
- 5 alunni hanno un'altezza di 145 cm;
- ....
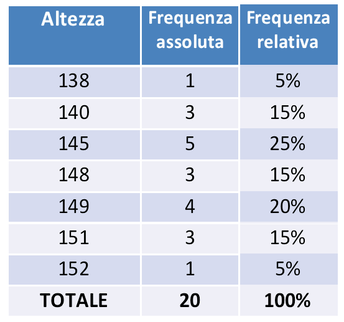
Questo che noi facciamo è quello di rapportare la frequenza di una determinata misura relativa ad una classe di 20 alunni.
Supponiamo di voler esprimere percentualmente i dati ottenuti, per poterli paragonare, ad esempio, agli alunni della classe terza di un'altra scuola.
Esprimere un dato come frequenza relativa vuol dire esprimerlo percentualmente, cioè rapportarlo al numero di casi totali che stiamo analizzando in questa analisi di dati.
Nella tabella qui a fianco ecco una colonna di valori della frequenza relativa che abbiamo ottenuto applicando la formula che sta qui sotto.
Supponiamo di voler esprimere percentualmente i dati ottenuti, per poterli paragonare, ad esempio, agli alunni della classe terza di un'altra scuola.
Esprimere un dato come frequenza relativa vuol dire esprimerlo percentualmente, cioè rapportarlo al numero di casi totali che stiamo analizzando in questa analisi di dati.
Nella tabella qui a fianco ecco una colonna di valori della frequenza relativa che abbiamo ottenuto applicando la formula che sta qui sotto.
Dalla frequenza percentuale a quella relativa
Se vuoi conoscere il valore della frequenza assoluta e hai a disposizione quella percentuale e il totale dei campioni che costituiscono la popolazione statistica, dovrai:
Frequenza assoluta = Frequenza percentuale · totale dei dati : 100